HCSR纵骨疲劳简化算法修正
2019-07-03
(中国船舶及海洋工程设计研究院,上海 200011)
由于交变载荷及应力集中现象的存在,疲劳破坏是船体结构发生海损事故的主要原因之一。《散货船和油舱结构共同规范》(下文简称HCSR)关于构件疲劳寿命的评估分为两种方法[1]:①简化算法;②有限元法。由于简化算法求解省时并且具有较为清晰的理论基础,因此结构工程师一般优先采用简化算法来评估船体纵骨端部连接处的疲劳寿命。除外部载荷外,影响纵骨疲劳寿命的主要内部因素是节点参数和节点位置。由于不同设计选用不同的节点参数,节点本身分布的位置各异,HCSR从简单实用的角度出发,对以上影响因素进行简化,因此,其计算精度受到一定影响。现有的研究已经发现HCSR纵骨疲劳简化算法评估结果与有限元法存在差异[2],并且与实船疲劳寿命定量上存在偏差[3],但并未深入探讨产生这种偏差的原因,也未提出相应的改进方法。为此,考虑对纵骨疲劳简化算法的理论背景进行梳理,研究应力集中系数与纵骨端部节点各设计参数的函数关系,并计入板架变形引起的纵骨上的局部应力成分,对HCSR纵骨疲劳简化算法进行适当修正。
1 纵骨疲劳计算方法
1.1 HCSR简化算法
纵骨端部连接疲劳寿命简化算法流程见图1。
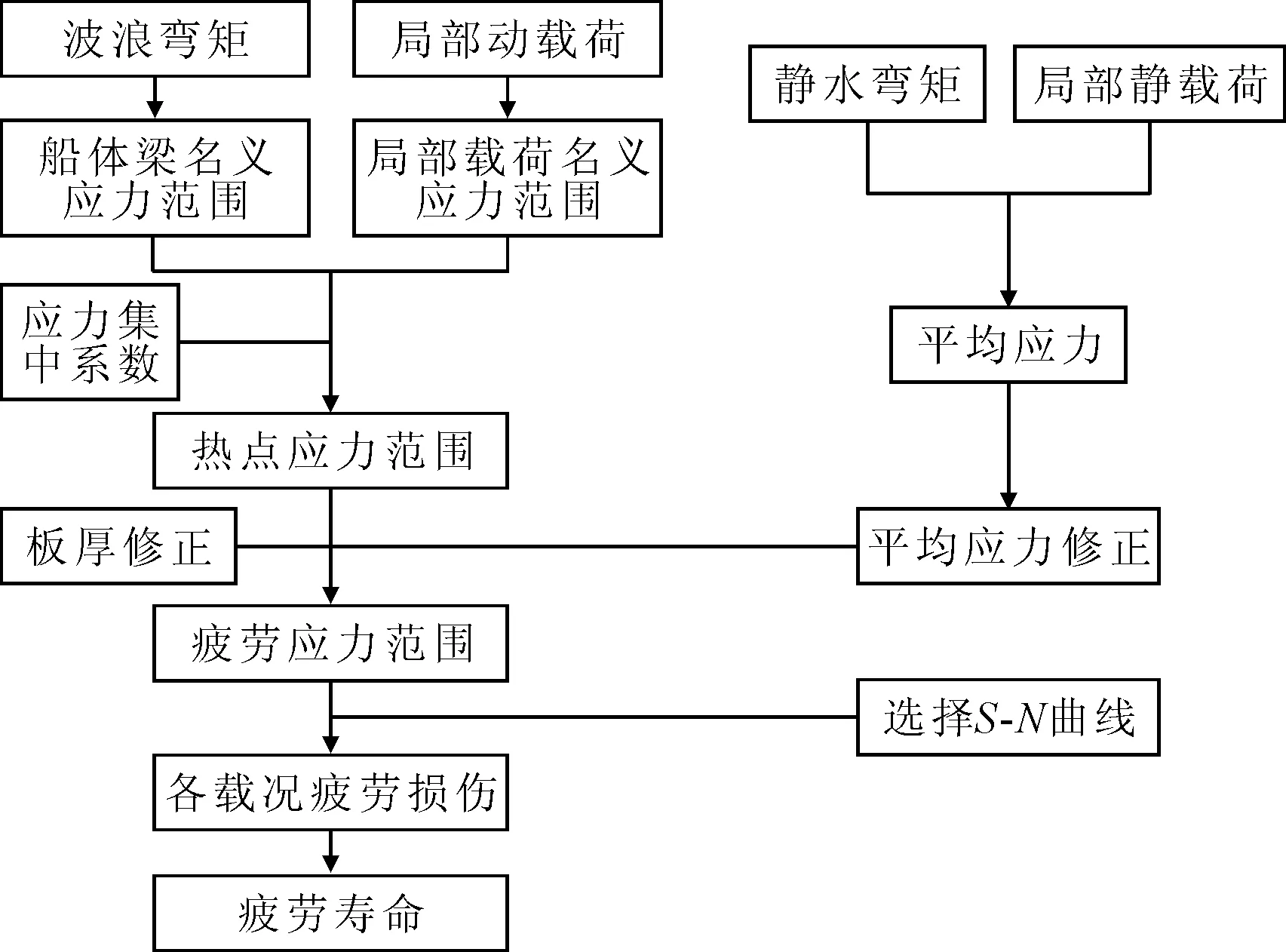
图1 纵骨疲劳简化算法流程
根据梁理论得出纵骨端部连接处的名义应力范围和平均应力,考虑一定的应力集中系数得到热点应力范围;对热点应力范围进行平均应力修正和板厚系数修正,得到疲劳应力范围;假设疲劳应力范围服从Weibull分布,根据Palmgren-Miner线性累积损伤理论,选择合适的S-N曲线,分别求出计算点在各装载工况下的疲劳损伤因子;最后对各装载工况下的疲劳损伤因子进行累加,得到计算点处的疲劳寿命。
船体纵骨端部连接处的纵向应力σ分为船体梁应力σ1和局部应力σ2,如果纵骨邻近横舱壁处,还应包括横舱壁相对位移引起的局部应力σD。采用经典梁理论仅能求出纵骨端部的名义应力,需要乘以应力集中系数方可得到端部连接处的热点应力,各纵向应力成分的表达式如下。
σ=σ1+σ2+σD
(1)
(2)
(3)
式中:Ka为轴向应力集中系数;Mv、Mh为船体梁垂向弯矩和水平弯矩;Iy、Iz为船体梁垂向惯性矩和水平惯性矩;z、zn为计算点处的垂向坐标,船体梁中和轴的垂向坐标;y为计算点处的横向坐标;Kb为弯曲应力集中系数;s、l为纵骨的间距和跨距;P为纵骨带板承受的压力;W为纵骨的剖面模数;x为计算点至跨距端点的距离。
σD的可以参考文献[1]和[4]中相关内容。
1.2 疲劳有限元法
采用有限元法计算纵骨端部连接疲劳的基本流程同简化算法一致,主要区别在图1中求解热点应力范围和平均应力的方法不同,HCSR简化算法采用经典梁理论并考虑一定的应力集中系数,有限元法则是采用有限元网格离散的数值方法。
因求解应力所用方法不同,导致由2种方法所得的疲劳寿命存在一定差异。本文中简化算法和有限元法的计算结果比较均基于相同的结构形式、材料特性和施加载荷等输入参数。有限元法作为求解应力的一种数值解法,离散的网格大小对计算结果有影响,但当网格足够精细时其计算结果收敛。本文中网格采用四节点四边形单元,网格尺寸为HCSR规定的板厚X板厚,采用该方法获得的应力结果可靠。
2 简化算法修正
分析HCSR纵骨疲劳简化算法的理论背景,发现其中对一些典型节点应力集中系数的选取过于简化,另外,也忽略了板架变形引起的纵骨局部应力成分。以上2种因素的叠加导致HCSR简化算法得到的疲劳应力范围存在一定误差,应当予以修正。
2.1 应力集中系数的修正
HCSR给出了一些典型纵骨端部连接节点的应力集中系数。对每一种类型的连接节点,应力集中系数通常是一个常数值。有限元数值分析发现,端部连接的应力集中系数与支撑纵骨的挺筋、背肘板的板厚和几何形状,以及纵骨的面板厚度等因素相关,并非一个恒定值。
图2给出了表1中节点(1)在疲劳热点B处应力集中系数与挺筋板厚ts和纵骨面板厚度tf的关系。比较发现:在纵骨面板厚度tf一定的情况下,挺筋厚度ts越大,则在其连接处的应力集中系数Ka和Kb越大;在挺筋厚度ts一定的情况下,纵骨面板厚度tf越大,则在其连接处应力集中系数Ka和Kb越小。即应力集中系数与挺筋厚度正相关,与纵骨面板厚度负相关。HCSR给出的应力集中系数常数值是一个平均值,在纵骨面板较厚且挺筋厚度相对较薄的情况下,计算结果较实际情况偏保守,反之则偏于危险。

图2 应力集中系数Ka、Kb与挺筋板厚ts和纵骨面板厚度tf的关系
图3给出了节点(1)在疲劳热点B处应力集中系数与表征支撑纵骨的挺筋趾端几何轮廓的角度Φ的关系(假设支撑纵骨的挺筋厚度和纵骨面板厚度恒定)。

图3 应力集中系数Ka、Kb与趾端角度Φ的关系
可以发现挺筋趾端的特征角度Φ越小,应力集中系数Ka和Kb越小。甚至当趾端角度Φ为负值时,应力集中系数可以减小至一个相当小的数值。在建造工艺允许的条件下,采用图4所示的内凹式圆弧趾端形式,可以最大程度地改善纵骨端部连接处的应力集中系数,从而提高连接处纵骨的疲劳寿命。

图4 内凹式圆弧趾端
这种处理方式与焊趾的根部打磨出来一个“凹坑”以提高焊趾处的疲劳寿命的工艺方法在原理上较为相似,见图5。

图5 焊趾根部打磨以提高疲劳寿命的工艺方法示意
对于实船结构设计中常用的纵骨端部连接节点,通过大量的有限元数值分析,并对计算结果进行拟合,得到应力集中系数关于纵骨上支撑挺筋的板厚ts、背肘板的板厚tb和几何形状(角度Φ),以及纵骨的面板厚度tf这些设计参数的函数表达式,见表1。
2.2 板架变形引起的局部应力
船体纵骨上的局部应力σ2包括由板架变形引起的局部应力σ2g[5-6]和骨材本身变形引起的局部应力σ2s。目前HCSR仅计入了骨材本身变形引起的局部应力σ2s(见式(3)),并未计入板架变形引起的局部应力σ2g。根据文献[1]中疲劳寿命计算公式可知,疲劳寿命与应力变化范围呈三次方关系,应力范围的计算误差会引起疲劳寿命计算误差的放大。特别对于散货船双层底板架,是由实肋板和纵桁组成的交叉梁系,其板架刚度相对较弱;再加之承受较大的舱内货物载荷或舷外水压力,板架变形会产生较大的局部应力,尤其是对于大型和超大型散货船而言σ2g与纵骨本身变形引起的局部应力σ2s同量级(比如,对某20.8万t级散货船的底部纵骨,σ2g=3.2 MPa,σ2s=5.1 MPa),不可忽略,否则会造成较大的疲劳寿命计算误差。另外,当板架变形引起的平均应力占总的平均应力比重较大时,对平均应力修正系数的影响也值得重视。
表1 常用纵骨端部节点的应力集中系数Φ

节点形式热点A热点BKa: 0.7(0.004 5Φ+1.13)tb1.56tf-0.67Kb: 0.66(0.006Φ+1.18)tb2.35tf-0.75Ka:0.7(0.004 5Φ+1.13)ts1.56tf-0.67Kb:0.66(0.006Φ+1.18)tb2.35tf-0.75Ka: 0.7(0.004 5Φ+1.13)tb1.56tf-0.67Kb: 0.66(0.006Φ+1.18)tb2.35tf-0.75Ka: 0.82(0.004 5Φ+0.96)ts1.4tf-0.63Kb: 0.9(0.006Φ+0.91)ts2.35tf-0.75Ka: 0.47h0.093tf0.06ts1.58tf-0.79Kb: 0.35h0.1tf0.12ts1.47tf-0.6Ka: 0.41h0.15ts1.36tf-0.78Kb: 0.34h0.16ts1.61tf-0.66Ka:0.57h0.064tf0.054ts1.69tf-0.85Kb:0.41h0.09tf0.08 ts1.78tf-0.6Ka: 0.41h0.15ts1.36tf-0.78Kb: 0.34h0.16ts1.61tf-0.66Ka: 0.47h0.093tf0.06ts1.58tf-0.79Kb: 0.35h0.1tf0.12ts1.47tf-0.6Ka: 0.7(0.004 5Φ+1.13)ts1.56tf-0.67Kb: 0.66(0.006Φ+1.18)tb2.35tf-0.75Ka: 0.85(0.01Φ+1.47)tw-0.18tb0.73tw-0.21Kb: 0.89(0.017Φ+1.65)tw-0.18tb0.6tw-0.17Ka: 0.85(0.01Φ+1.47)tw-0.18ts0.73tw-0.21Kb: 0.89(0.017Φ+1.65)tw-0.18ts0.6tw-0.17
因此,纵骨的局部纵向应力计算应计入板架变形引起的局部应力成分,不靠近横舱壁船体纵骨总的纵向应力表达式为
σ=σ1+σ2g+σ2s
(4)
式中:σ1见式(2);σ2s见式(3);σ2g与板架刚度和承受的载荷有关,其计算比较复杂,由于船体结构设计的差异性,与有限元法得到的计算结果始终无法很好地吻合,建议通过构建三维梁系模型或者有限元模型数值求解。
3 计算结果对比
为了验证文中所提出的修正方法的合理性,选取20.8万t级散货船和30万t级VLCC两型船(见图6、7),分别采用修正前、修正后简化算法和有限元法对图6和图7中标记的纵骨进行疲劳强度评估。其中,σ2g的计算结果通过构建三维梁系模型求得。

图6 20.8万t级散货船纵骨疲劳强度评估点
图6中,纵骨1、3和5采用表1中节点(1)的连接形式,纵骨2采用节点(2)的连接形式,纵骨4采用节点(6)的连接形式。
图7中,纵骨1和5采用表1中节点(5)的连接形式,纵骨2采用节点(2)的连接形式,纵骨3采用节点(1)的连接形式,纵骨4采用节点(3)的连接形式。

图7 30万t级VLCC纵骨疲劳强度评估点
将修正前和修正后简化算法的评估结果与有限元法评估结果进行对比,见图8、9。

图8 不同计算方法疲劳评估结果比较(20.8万t级散货船)

图9 不同计算方法疲劳评估结果比较(30万t级VLCC)
由图8、9中可知,船体底部区域纵骨(特别是散货船)采用修正前简化算法的疲劳评估结果与有限元法评估结果差异较大,一部分原因是应力集中系数的取值为常数,与实际情况不符;另一部分原因是因为忽略了板架变形引起的局部纵向应力成分。考虑到船体甲板区域纵骨采用修正前简化算法的疲劳评估结果与有限元法评估结果差异相对小,所以认为主要是由应力集中系数的取值与实际情况不符引起。
图8、9的对比表明,修正前的简化算法评估结果与有限元评估结果相差较大,且结果偏大和偏小的可能性均存在;修正后的简化算法评估结果与有限元评估结果相差较小,计算误差在可以接受的范围内。
4 结论
为提高纵骨疲劳简化算法的精度,建议从两个方面对HCSR纵骨疲劳简化算法进行修正。①对应力集中系数进行修正,考虑支撑纵骨的挺筋、背肘板的板厚和几何形状,以及纵骨的面板厚度这些设计参数对连接处应力集中系数的影响,给出相应的函数表达式;②建议计算纵骨局部应力时计入板架变形引起的局部应力成分。
