面向在轨服务任务的气囊型软体机械臂运动学建模与分析

刘红卫，张 翔，2，黄奕勇，陈小前

(1.军事科学院国防科技创新研究院，北京100071； 2.国防科技大学空天科学学院，长沙410073)

1 引言

随着在轨服务技术自主化、智能化程度的不断提高，在轨加注、模块更换、在轨组装、在轨维修等空间操作对机械臂的需求日益增加，需要机械臂更加灵巧、智能，适应空间高动态、复杂、非结构环境。 日本工程试验卫星-7(Engineering Test Satellite VII，ETS-VII)是世界上首个装有机械臂的卫星系统，机械臂长2 m，具有六自由度、验证卫星模块更换、在轨桁架组装、装配试验天线等技术[1]。 德国DEOS 在轨服务任务使用机械臂抓捕非合作翻滚目标，在预定的再入走廊使捕获卫星离轨[2-3]。 2014 年，美国启动了Restore-L 项目，验证低轨合作和非合作目标在轨燃料加注技术，计划2020 年发射，与目标卫星LandSat-7 开展交会对接，使用机械臂完成燃料加注操作[4-5]。 美国DARPA 开展了“地球同步卫星机器人服务(Robotic Servicing of Geosynchronous Satellites，RSGS)”项目，RSGS 飞行器上装有两个机械臂，可以与航天器实现交会对接，预计2021 年发射，开展在轨组装、维修、检查、改变位置、燃料加注等空间操作[6]。 这些任务的机械臂采用刚性连接，利用刚性杆和活动关节实现多自由度空间运动。

近年来，不同研究机构开展了基于电活性聚合物、形状记忆合金、气动人工肌肉、流体、水凝胶等材料的软体机械臂研究，在未来在轨服务方面显示出了广阔的应用前景，成为机械臂研究领域的热点方向[7]。 相比于传统的刚性连接机械臂，软体机械臂具有质量轻、自由度多、可实现大范围变形、对空间非结构环境适应能力强、安全柔性接触等优势[8]。 德国Festo 公司研制了仿象鼻机械臂，由多个中空的柔性密闭管道组成，通过在管道中施加不同的气压来控制机械臂运动[9]。 Qi 等[10]研究了多关节充气机械臂的动力学建模与控制问题，该软体机械臂重量为50 g，通过充气控制机械臂运动，可与人体安全接触。 此外，不同学者研究了软体抓手、类章鱼臂、类蠕虫、软体鱼、类蛇体等形态的软体机器人[7，11]。 张翔等[12]针对未来在轨服务任务需求，提出了基于波纹管串并联方式的软体机械臂方案，如图1(a)所示[12]。 每个波纹管单独充气控制，通过气压变化带动波纹管伸缩。 3 个波纹管并联形成一节软体驱动器，波纹管中不同的气压组合对应软体驱动器不同的空间位置。 3 节软体驱动器串联并增加末端软体抓手，构成软体机械臂，可实现多冗余自由度的大范围运动和目标抓取，在空间在轨服务方面具有重要的应用前景，图1(b)是设计并搭建的软体机械臂地面样机。

图1 软体机械臂Fig.1 The soft manipulator

与传统刚性连接的机械臂不同，软体机械臂运动学建模复杂，需要在考虑软体材料力学行为的基础上，结合软体结构特征、本构关系以及约束条件建立运动学模型。 本文针对上述气囊型软体机械臂方案，开展高精度运动学建模与仿真分析，以期为后续软体机械臂控制提供模型基础。

2 气囊型软体机械臂建模

2.1 问题描述

软体机械臂由3 节软体驱动器串联组成(见图1)，每节驱动器由3 个对称布置的波纹管并联组成，其横截面如图2 所示。 驱动器与驱动器之间采用刚性约束框连接，每节驱动器内并联的波纹管也是由一系列刚性约束框连接。 在机械臂运动过程中，刚性约束框始终保持整体的空间指向，不会发生弯曲变形。 在相邻两个刚性约束框之间，由软体材料构成的气囊可以伸缩或弯曲。 每个波纹管采用单独的气压控制，通过控制不同的气压组合实现机械臂复杂的空间运动。 下面建立波纹管输入气压与软体机械臂末端运动之间的运动学关系。

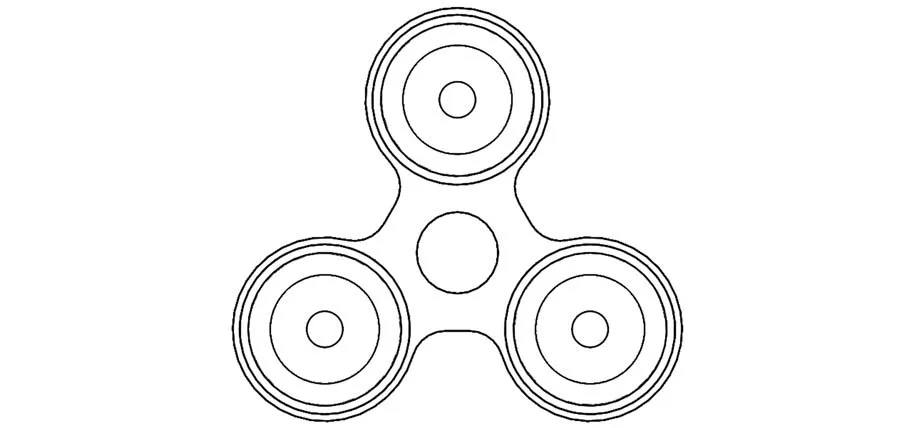
图2 并联波纹管的横截面Fig.2 The cross section of parallel bellows

2.2 无刚性约束框的单节软体驱动器模型

为便于建模，首先考虑无刚性约束框下的单节软体驱动器运动学建模问题，如图3 所示。 3个波纹管A、B、C 对称并联，相邻两个波纹管中心之间的水平距离均为a， 下端固定，上端由刚性框连接，保证3 个波纹管上端面具有相同的空间指向。 除上下端面外，波纹管之间不存在约束和连接。 在无充气状态下，3 个波纹管的长度均为L0。

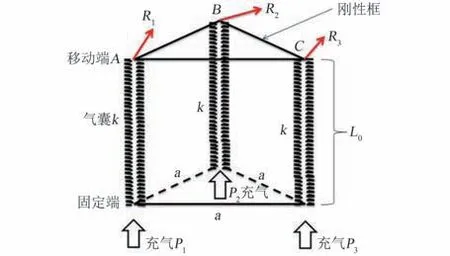
图3 无刚性约束框的单节软体驱动器Fig.3 A single soft driver without the rigid frame

当波纹管充气时，仅考虑沿波纹管轴向的伸长变化，不考虑沿径向的变化。 设3 个波纹管的弹性系数为k， 输入气压分别为P1、P2、P3， 每个波纹管伸长产生的弹力分别为F1、F2、F3，伸长量分别为ΔL1、ΔL2、ΔL3，在弹性变形假设下有平衡关系如式(1)：

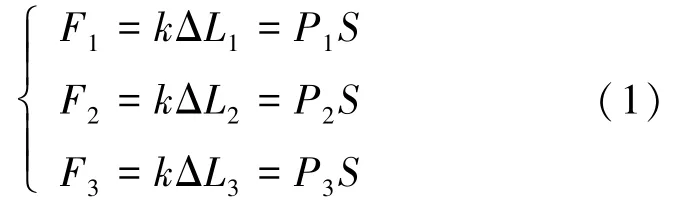
其中，S 是波纹管内部的横截面积。 如果不存在上端刚性框，3 个波纹管的长度如式(2)所示：

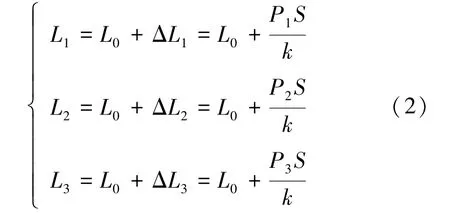
上端刚性约束框的力学效果有两个：①使3个波纹管上端A、B、C3 点仍然构成等边三角形，边长为a；②使3 个波纹管上端面法向具有相同的空间指向。 以固定端平面为xy 平面，建立直角坐标系，如图4 所示。 A0、B0、C0分别为3 个波纹管的固定端，3 点构成等边三角形，边长为a。 以B0点为坐标原点，x 轴垂直于A0C0向下，y 轴水平向右，z 轴垂直于纸面向外，构成右手直角坐标系。 在该坐标系中，A0、B0、C0的坐标如式(3)所示：

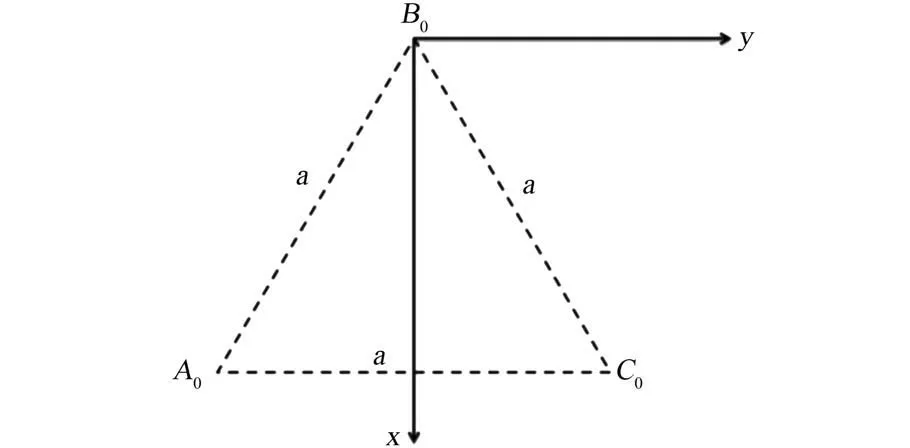
图4 直角坐标系Fig.4 Cartesian coordinate system

在未充气状态下，3 个波纹管上端点A、B、C的坐标分别为 A：设上端刚性框对3 个波纹管的作用力分别为R1、R2、R3，其方向位于约束框平面内。 在R1、R2、R3的作用下，3 个波纹管上端产生的挠度如式(4)所示：

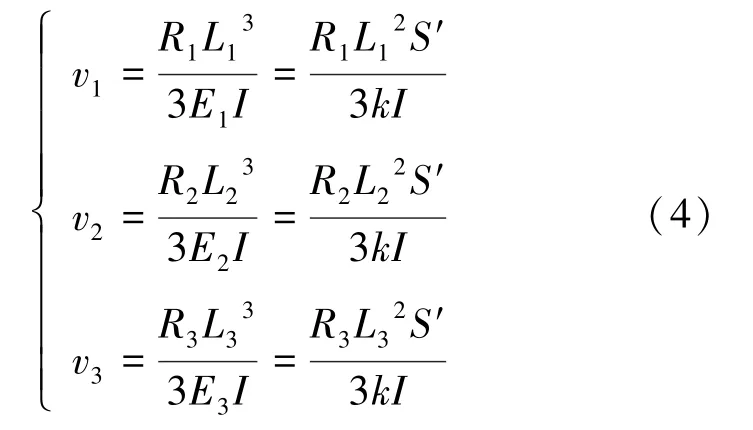
其中，E 为弹性模量，I 为惯性矩，EI 为弯曲刚度，S′为波纹管壁的横截面积，即承受轴向拉压的有效面积。 对于外半径为R、内半径为r 的圆环截面，其惯性矩如式(5)所示：

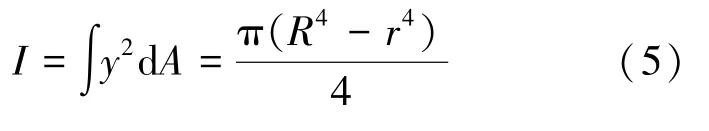
在R1、R2、R3的作用下，3 个波纹管上端产生的转角如式(6)所示：

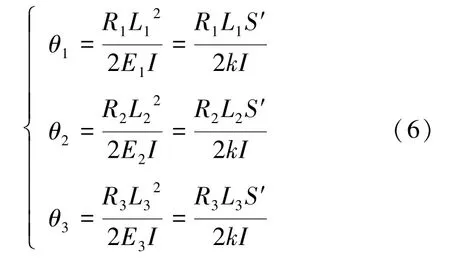
3 个波纹管上端点A、B、C 具有相同的法向指向，意味着这些波纹管上端面具有相同的转角，即θ1＝θ2＝θ3，从而得到式(7)：

A、B、C 具有相同的法向指向也意味着，具有挠度的3 个波纹管在xy 平面内的投影方向平行。设从x 轴起算沿逆时针到投影的角度为α，则充气后3 个波纹管上端点坐标如式(8)所示：

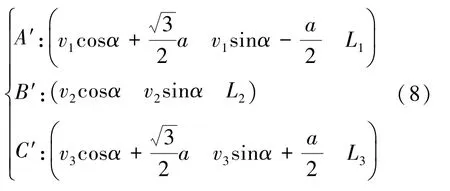
根据约束条件A′B′＝B′C′＝C′A′＝a，得到式(9)～(11)：

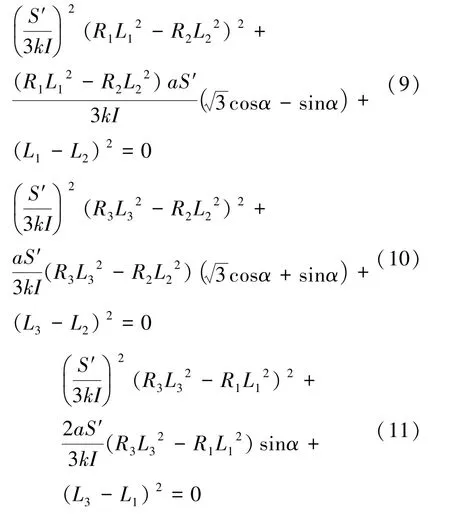
方程(7)和(9)～(11)共5 个方程，需要求解的未知数有4 个，分别为R1、R2、R3、α， 可以验证这5 个方程中冗余度为1，即有一个方程是多余的。 为便于表示，设式(12)：

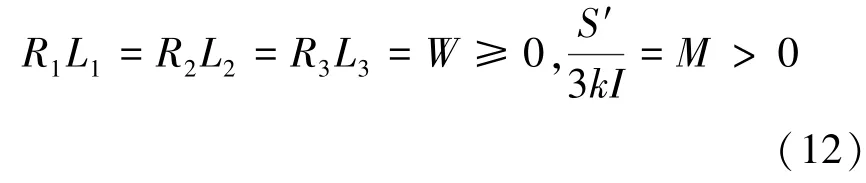
联立方程(7)和(9)～(11)，得到角度α 如式(13)：

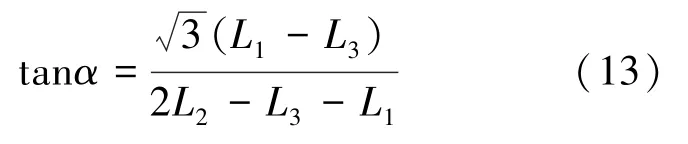
角度α 取值范围如式(14)所示：

同时，根据方程(7)和(9)～(11)，得到W 如式(15)～(16)：

1)当ΔL1≠ΔL3时：

2)当ΔL1＝ΔL3≠ΔL2时：

根W 中包含2 个正数解，取其较小者为方程的实际解，它对应较小的挠度。

根据式(2)，由3 个波纹管的输入气压P1～P3，得到波纹管伸长后的长度L1～ L3。 由上述方程(13)～(16)可以得到R1、R2、R3、α， 然后由式(4)得到3 个波纹管的挠度v1～ v3，进而由式(8)计算得到波纹管上端A′、B′、C′ 的空间位置，这样就建立了从波纹管输入气压P1～ P3到波纹管上端A′、B′、C′位移之间的数学关系。

2.3 带刚性约束框的单节软体驱动器运动学模型

对于带有刚性约束框的单节软体驱动器，仍然是由3 个波纹管对称并联组成，但是沿波纹管长度方向均匀布置了N 个刚性约束框，保证该位置处的3 个波纹管中心点组成边长为a 的等边三角形。 N 个刚性约束框将波纹管划分为等距离的各个小段，这些小段是完全相同的，具有相同的输入气压。

从固定端开始，自下而上考虑波纹管每一小节在刚性约束框下的力学行为。 由对称性可知，每一小节相对其底端刚性约束框的运动轨迹均是相同的。 不妨考虑建立在固定端和第一个刚性约束框上的直角坐标系。 与图4 中直角坐标系建立规则相同，分别取B0、B1为原点，原点指向三角形对边中点的方向为x 轴，取固定端和刚性约束框平面为xy 平面，x 轴逆时针转动90°为y 轴， xyz构成右手直角坐标系，如图5 所示。

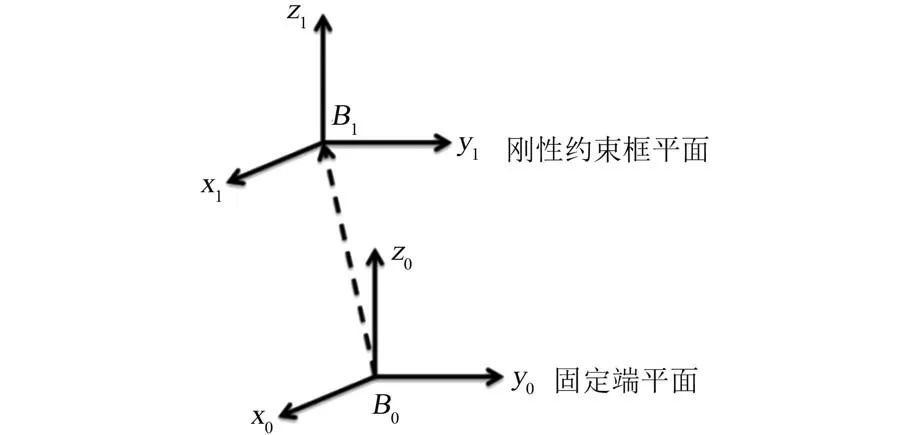
图5 相邻两个面上的直角坐标系Fig.5 Cartesian coordinate system on two adjacent faces

在图5 中，固定端平面和刚性约束框平面之间存在一段波纹管，设波纹管的弯曲方向为α，末端弯曲角度为θ，则由x0y0z0到x1y1z1的旋转矩阵为H，转换过程如式(17)所示：

考虑到x0y0z0和x1y1z1坐标系的原点不重合，因而式(17)需要调整为式(18)所示形式：

其中，rB0B1是在x0y0z0坐标系中表示的由B0到B1的矢量。 假设带刚性约束框的单节软体驱动器末端中心在其刚性约束框坐标系中的坐标为r*，该软体驱动器共有N 节，则r*在固定端坐标系x0y0z0中的坐标表示为式(19)：

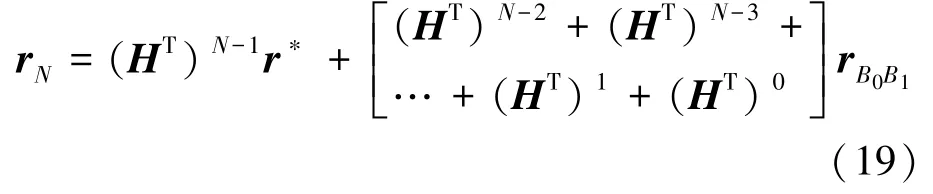
2.4 带刚性约束框的多节软体驱动器串联模型

以3 节带有刚性约束框的软体驱动器串联为例，建立软体机械臂的运动学模型。 串联部位采用刚性约束，约束部件厚度分别为T1-2、T2-3。 设3 节软体驱动器中的波纹管外半径分别为rout，1、rout，2、rout，3， 内半径分别为rin，1、rin，2、rin，3，单节波纹管的原始长度分别为L0，1、L0，2、L0，3，弹性系数分别为k1、k2、k3， 相邻两个波纹管中心之间的水平距离分别为a1、a2、a3。 第1节软体驱动器中3 个波纹管施加的气压分别为P11、P12、P13，第2 节中3 个波纹管施加的气压分别为P21、P22、P23， 第3 节中3 个波纹管施加的气压分别为P31、P32、P33， 3 个软体驱动器的节数分别为N1、N2、N3。

根据2.3 节模型，计算得到每节软体驱动器中各段相对底部坐标系的三维坐标，其中3 节软体驱动器底部坐标系分别为x01y01z01、x02y02z02、x03y03z03。 已知第2 节软体驱动器上各段在x02y02z02坐标系上的坐标表示为r*2 ， 将其转换到x01y01z01坐标系中，得到式(20)：

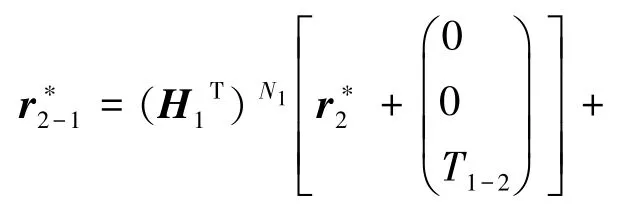
其中，H1＝H1(α1，θ1)， (rB0B1)1括号外面的下标1表示是在第一节软体驱动器中计算得到的。同理，得到第3 节软体驱动器上的坐标转换到x02y02z02上的坐标如式(21)：

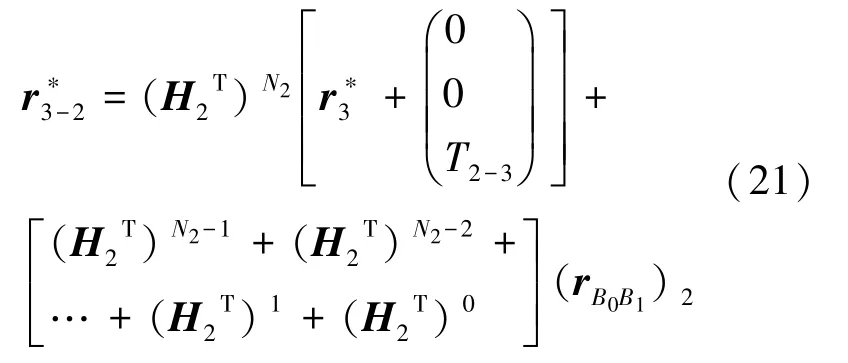
其中，H2＝H2(α2，θ2)， (rB0B1)2括号外面的下标2 表示是在第2 个软体驱动器中计算得到的。 这样，根据式(20)和(21)，得到了带有刚性约束框的3 节软体驱动器串联后末端中心位移与波纹管输入气压之间的关系，从而建立了气囊型软体机械臂的运动学模型。

3 仿真与分析

3.1 仿真验证

在典型的软体机械臂系统参数下，进行机械臂末端运动仿真分析。 设整个气囊型软体机械臂由3 节软体驱动器组成，每节驱动器的节点数分别为16、16、16，第1、2 节软体驱动器刚性连接的厚度为20.4 mm，第2、3 节软体驱动器刚性连接的厚度也为20.4 mm。 取3 节驱动器中波纹管的物性参数相同，分别是波纹管外半径26.2 mm、内半径25 mm、单段波纹管未充气时原始长度19.125 mm、单段波纹管弹性系数2.0×104N/m，两个波纹管中心点的距离为75 mm。 在上述机械臂物性参数设置下，给出机械臂在气压输入下的运动仿真算例。设第1 节软体驱动器中3 个波纹管的输入压力变化范围分别为(0.0～2.0)×105Pa、(0.0～2.0)×105Pa、(0.0～0.0)×105Pa，第2 节软体驱动器中3 个波纹管的输入压力变化范围分别为(0.0～0.0)×105Pa、(0.0～0.0)×105Pa、(0.0～2.0)×105Pa，第3 节软体驱动器中3 个波纹管的输入压力变化范围分别为(0.0～2.0)×105Pa、(0.0～2.0)×105Pa、(0.0～0.0)×105Pa。 在气压初始状态和末状态之间按照线性关系取10 个点，形成时间序列。 计算得到在该时间序列下的软体机械臂运动轨迹，如图6～9所示。 其中，圆圈代表机械臂上各个质量点，红色部分表示第1 节驱动器，其底端固定，蓝色部分表示第2 节驱动器，黑色部分表示第3 节驱动器，其末端处于自由状态。 可见，相对于传统刚性连接机械臂，软体机械臂运动更加灵活，通过多冗余自由度设计可以实现对复杂非规则、非结构环境的适应。

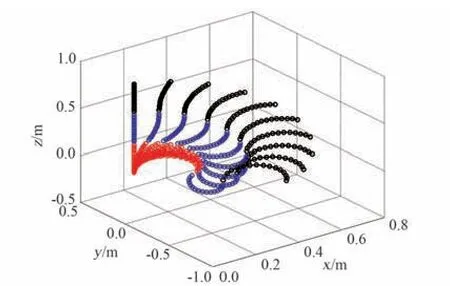
图6 软体机械臂各点运动轨迹(三维视图)Fig.6 The motion of each point on the soft manipulator (3D view)

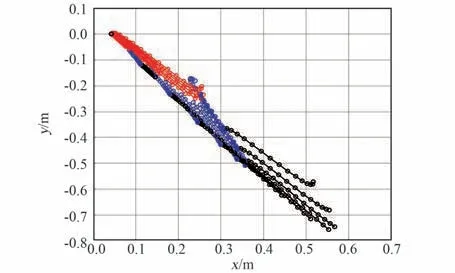
图7 软体机械臂各点运动轨迹(XY 视图)Fig.7 The motion of each point on the soft manipulator (XY view)

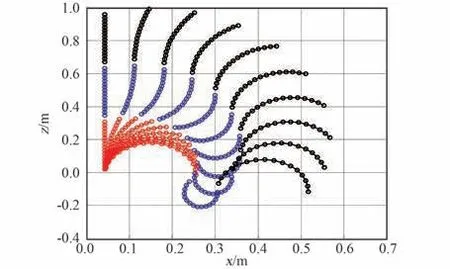
图8 软体机械臂各点运动轨迹(XZ 视图)Fig.8 The motion of each point on the soft manipulator (XZ view)

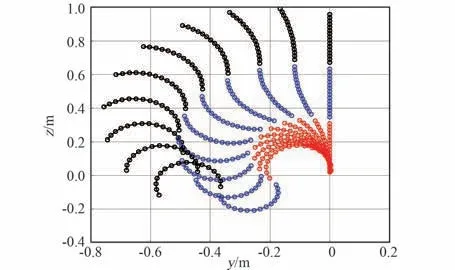
图9 软体机械臂各点运动轨迹(YZ 视图)Fig.9 The motion of each point on the soft manipulator (YZ view)

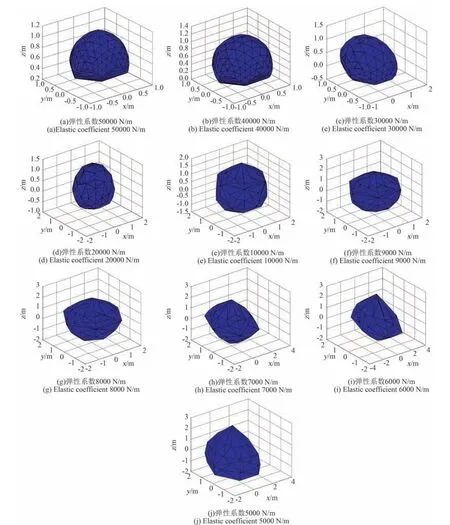
图10 气囊型软体机械臂末端点的运动包络Fig.10 The motion envelope of the end point of the soft inflatable manipulator

3.2 机械臂末端运动包络分析

下面给出软体机械臂末端的运动包络。 软体机械臂的物性参数在3.1 节给出，波纹管压力的变化范围为(0.0～1.1)×105Pa。 软体机械臂中波纹管的弹性系数决定了机械臂末端运动范围。 在软体机械臂其他物性参数不变的情况下，单独改变波纹管的弹性系数，使其在5×103～5×104N/m 范围内变化，那么利用第2 节建立的机械臂模型可以得到机械臂末端运动包络，如图10 所示。

由图10 可知，软体机械臂末端运动包络呈现出如下特征：

1)软体机械臂末端运动包络的尺寸与机械臂弹性系数有关，弹性系数越大，则其刚度越大，末端运动范围越小；反之，末端运动范围越大；

2)软体机械臂末端运动包络的形状与弹性系数、波纹管布局有关。 当弹性系数较大时(大于4×104N/m)，运动包络的形状明显受波纹管并联方式的影响，运动包络在xy 平面的投影呈正六边形，这是由3 个波纹管对称并联形成软体驱动器的设计布局决定的；当弹性系数进一步降低时(1×104～3×104N/m)，弹性系数与波纹管布局对机械臂末端包络的影响基本相同，运动包络呈现各向同性的形状特征；当弹性系数降低到足够小时(小于1×104N/m)，机械臂末端运动包络也明显受到波纹管布局方式的影响，呈现出规则的空间多面体结构。

软体机械臂末端运动包络的尺寸和形状特征分析对机械臂设计具有重要的参考价值。

4 结论

1)本文提出的气囊型软体机械臂采用了3节波纹管对称并联形成软体驱动器、3 段软体驱动器串联形成机械臂的实现方案，自由度为9，通过独立控制各个波纹管内的压力实现机械臂复杂空间运动。

2)基于波纹管局部伸缩变形的线弹性假设和弯曲变形的弹性梁假设，可以推导构建机械臂运动学模型，用来描述波纹管气压输入与机械臂运动之间的关系。

3)运动学仿真计算表明，相对于传统刚性连接机械臂，软体机械臂运动更加灵活，具有大范围弯曲变形、适应复杂非结构环境的运动优势。

4)软体机械臂末端运动包络分析表明，包络尺寸与波纹管弹性系数有关，弹性系数越大，包络范围越小；包络形状与波纹管布局、波纹管弹性系数有关，弹性系数在1×104～3×104N/m 范围时，包络形状基本呈各向同性，弹性系数过大或过小时包络形状呈现为与波纹管布局相关的规则几何体。

参考文献(References)

[1]Yoshida K.Engineering test satellite VII flight experiments for space robot dynamics and control： theories on laboratory test beds ten years ago，now in orbit[J].The International Journal of Robotics Research， 2003， 22(5)： 321-335.

[2]Reintsema D， Thaeter J， Rathke A， et al.DEOS-the German robotics approach to secure and de-orbit malfunctioned satellites from low earth orbits[C]/ /Proceedings of the i-SAIRAS.Sapporo， Japan： Japan Aerospace Exploration Agency(JAXA)， 2010： 244-251.

[3]Flores-Abad A， Ma O， Pham K， et al.A review of space robotics technologies for on-orbit servicing[J].Progress in Aerospace Sciences， 2014， 68： 1-26.

[4]Gefke G， Janas A， Chiei R， et al.Advances in robotic servicing technology development[C]/ /AIAA SPACE 2015 Conference and Exposition， 2015： 4426.

[5]Reed B B， Bacon C， Naasz B J.Designing spacecraft to enable robotic servicing[C]/ /AIAA SPACE and Astronautics Forum and Exposition， 2017： 5255.

[6]Ashman B， Bauer F H， Parker J， et al.GPS operations in high Earth orbit： recent experiences and future opportunities[C]/ /2018 Space Ops Conference.Marseille，France，2018-2568.

[7]Jing Z L，Qiao L F，Pan H，et al.An overview of the configuration and manipulation of soft robotics for on-orbit servicing[J].Science China Information Sciences， 2017， 60：050201.

[8]Sanan S.Soft Inflatable Robots for Safe Physical Human Interaction[D].Pittsburgh， Pennsylvania， U.S.： Carnegie Mellon University， 2013.

[9]Nordmann A， Rolf M， Wrede S.Software abstractions for simulation and control of a continuum robot[C]/ /Simulation，Modeling， and Programming for Autonomous Robots.Springer， Berlin， Heidelberg： SIMPAR， 2012.

[10]Qi R， Khajepour A， Melek W W， et al.Design， kinematics，and control of a multi joint soft inflatable arm for human-safe interaction[J].IEEE Transactions on Robotics， 2017， 33(3)： 594-609.

[11]Laschi C， Mazzolai B， Cianchetti M.Soft robotics： technologies and systems pushing the boundaries of robot abilities[J].Science Robotics， 2016， 1(1)： 3690.

[12]张翔， 黄奕勇， 陈小前， 等.一种模块化的气控型软体伸缩机械臂： 中国国家发明专利， CN201810424655.X[P].2018.10.09.Zhang X， Huang Y Y， Chen X Q， et al.A modular air-controlled soft flexible manipulator： Chinese national invention patent， CN201810424655.X[P].2018.10.09.(in Chinese)