模拟不同重力水平下多种步态中下肢关节运动特征研究

罗诗瑶，杨洪瑞，尚 坤

(中国航天员科研训练中心人因工程国防重点实验室，北京100094)

1 引言

未来载人航天任务将向着月球及深空方向发展，人类不仅要重返月球并长期驻守月球基地，还要登陆火星和进行更远的深空探测，将面临更为严苛的空间环境，其中必不可少的是航天员的个体防护装备—星际航天服。 星面的出舱活动将更加频繁、任务类型更加复杂，这对星际航天服的环境防护、工效和生命保障等能力提出了更高的要求[1]。

用于星面探索活动的星际航天服和用于空间轨道出舱的舱外航天服存在很大差异。 一是使用环境不同：近地轨道为失重环境，月球和火星表面为低重力环境，月球表面重力加速度为1/6g，火星表面为1/3g，着服航天员在星面出舱时需能够站立并实现步态行走[2]；此外，月球/火星的地形崎岖并具有较大的坡度，裸露着大量的岩石碎块[3]，着服航天员需在崎岖地形上行走。 二是任务模式不同：月面/火星的出舱活动将开展大量的科学试验和地质考查，还有建立月球/火星基地的可能。 当前轨道出舱活动主要依靠上肢和手套开展作业，对舱外航天服下肢活动性要求不高[2，4]。航天员在执行星际探索任务，如低重力环境中的徒步行走、使用各种工具进行月面样本收集以及在月球表面长距离驾驶月球车等，均需要下肢活动能力支持，这就对星际航天服下肢的活动性提出了更高的要求[5]。 从某种意义上说，星际航天服下肢的活动性将决定航天员的活动范围和任务完成能力[6]。

为了合理配置服装关节以满足未来星际探索任务下肢活动性需求，首先要将人自身的能力和局限性作为设计过程的关键要素，明确人的运动能力，尤其是在不同重力环境下，典型步态的运动特征将会发生怎样的变化。 Ackermann 等[7-8]采用骨骼肌模型进行了一系列的步态预言仿真模拟，研究发现在低重力条件下(如月球或火星表面)，采用行走与蹦跳相结合的步态策略更高效且不易疲劳。 Minetti 等[9-10]用skipping 描述了阿波罗登月计划中航天员所采用的一种特殊步行方式，这是基于在低重力环境下能量消耗较小的目标而选用的一种方式。 然而，目前相关的实验研究报道较少。 本文针对星际探索任务中的典型步态动作，开展常规重力、模拟月球和火星重力条件下人体下肢运动测量实验，探索不同重力环境下平地与坡地行走和慢跑时关节活动范围等运动特征变化，为提出满足载人登月(火星)活动性需求的星际航天服下肢关节配置方案提供依据，为开展星际航天服下肢关节设计提供基础实验数据。

2 实验方法

2.1 测试样本

共选取9 名成年男性受试者，年龄26.33 ±3.67 岁，身高174.33±5.67 cm，体重72.78±5.98 kg。身体健康，无任何关节、肌肉病变。

2.2 测试设备

实验中采用美国Noraxon MYO Motion 的惯性运动捕捉分析系统，分别在受试者腰部、大腿、小腿和足部安装惯性传感器，采样频率100 Hz，如图1 所示，受试者在跑步机上进行不同速度和坡度的行走和跑步活动。

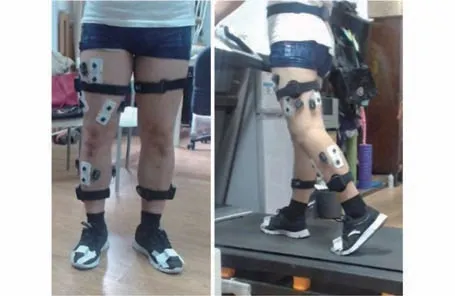
图1 受试者惯性传感器测点分布Fig.1 Distribution of inertia sensor measurement locations in the test subject

本研究设计了一种悬吊式低重力模拟装置，如图2 所示，通过垂直悬吊的方法实现低重力模拟，利用配重或弹力绳的方式进行重力补偿，根据不同重力水平模拟需求以及受试者自身体重，选择相应的配重或改变弹力绳的弹力。 受试者着悬吊背带实现步态运动中持续向上的拉力，以抵消部分重力作用。 配重或弹力绳力加载范围为0～85 kg。

2.3 测试流程

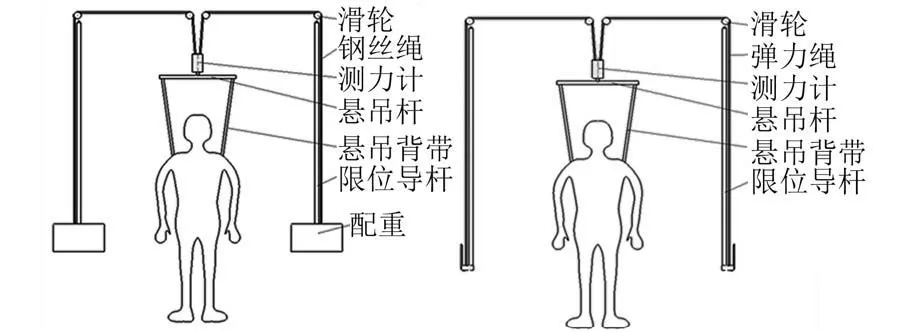
图2 悬吊式低重力模拟装置示意图Fig.2 Schematic diagram of the suspension type low gravity simulation device

每名受试者分别进行常规重力(1g)、模拟火星重力(1/3g)和模拟月球重力(l/6g)3 种重力环境下的行走和跑步测试。 每种重力环境下跑步机均设置3 种速度等级，其中，平地行走速度4 km/h，平地慢跑速度7 km/h，坡地行走速度3.6 km/h、坡度15°。 在测试数据正式采集前所有受试者均进行10 min 的热身，熟悉实验条件，以采取适应后最舒适的姿势进行实验。 当受试者达到每个要求的运动等级平稳至匀速，并持续1 min 后进行相应信号的采集，连续记录15～20 个完整的步态周期。

2.4 数据处理

采用Noraxon MR3 3.10.2 软件建立图3 所示的运动学模型，对惯性传感器测量数据进行分析，得到下肢关节活动角度。

图3 运动学分析模型Fig.3 The kinematic analysis model

实验数据采用均值±标准差的方式表示。 采用单因素重估测量方差分析确定不同重力水平对不同动作各种指标的影响，Post Hoc 检验采用LSD 法，显著性水平定为一类误差概率不大于0.05，所有统计分析应用SPSS 19.0 完成。

3 结果与讨论

3.1 关节活动范围

根据人体肢体运动定义，髋关节的运动可分解为矢状面上的屈曲/伸展、冠状面上的内收/外展以及横截面上的内旋/外旋；膝关节主要考虑小腿绕膝关节的冠状轴所做的屈伸运动，当小腿屈曲时，膝关节可绕垂直轴作微小的旋转运动，但活动幅度不大，忽略不计；踝关节同髋关节类似，分解为矢状面上的背屈/跖曲、冠状面上的内翻/外翻以及横截面上的内旋/外旋运动[11]。

3.1.1 平地行走

3 种重力水平下，平地行走(4 km/h)时人体下肢髋、膝和踝关节的关节活动范围如图4 所示。从图中可以看出，平地行走时，下肢各关节在矢状面上的屈曲/伸展活动范围远大于冠状面的内收/外展和横截面上的内旋/外旋活动。 其中，膝关节屈伸活动范围最大，达到67°以上。

平地行走时，重力水平对髋关节、膝关节的活动范围有显著影响。 模拟低重力条件下，髋关节屈曲/伸展(P ＜0.001)、内收/外展(P ＜0.001)、内/外旋(P＜0.05)的活动范围均明显减小，膝关节屈曲/伸展活动范围也显著减小(P ＜0.001)。重力水平对踝关节活动范围有较大影响，与髋、膝关节不同的是，重力水平降低后，踝关节背屈/跖屈、内/外旋活动范围有所增大，内/外翻活动范围减小，但未达到统计学显著性差异水平(P ＞0.05)。

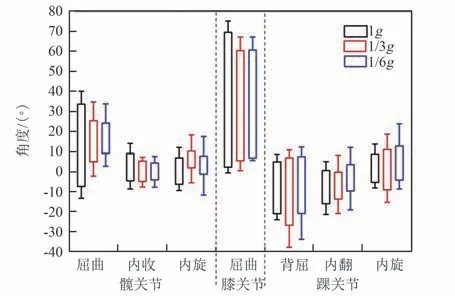
图4 平地行走(4 km/h)时髋、膝、踝关节活动范围Fig.4 The range of motion in hip， knee and ankle joints during ground walking (v=4 km/h)

3.1.2 平地慢跑

3 种重力水平下，平地慢跑(7 km/h)时人体下肢髋、膝和踝关节的关节活动范围如图5 所示。与行走相比，平地慢跑时表现出相似的运动规律，下肢各关节在矢状面上的屈曲/伸展活动远大于冠状面的内收/外展和横截面上的内旋/外旋活动，在髋关节中表现得最为明显。 各关节中以膝关节屈伸活动范围最大，平均值达67°。 此外，平地慢跑时各重力水平下踝关节背屈/跖屈活动范围均大于行走时的相应值。 平地慢跑时，重力水平对髋关节的活动范围有显著影响，模拟低重力条件下，髋关节在各个平面上的活动范围均明显减小(屈曲/伸展P＜0.001、内收/外展P＜0.005、内/外旋P＜0.05)。 重力水平对膝关节和踝关节的活动范围有较大影响，重力水平降低后膝关节活动范围减小，踝关节背屈/跖屈和内/外旋活动范围有所增大，内/外翻活动范围减小，但变化程度均未达到统计学显著性差异水平(P＞0.05)。

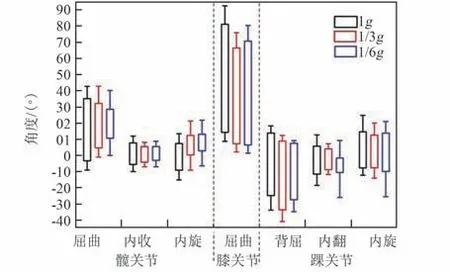
图5 平地慢跑(7 km/h)时髋、膝、踝关节活动范围Fig.5 The range of motion in hip， knee and ankle joints during ground jogging (v=7 km/h)

3.1.3 坡地行走

3 种重力水平下，坡地行走(15°， 3.6 km/h)时人体下肢髋、膝和踝关节的关节活动范围如图6 所示。 同样地，坡地行走时，下肢各关节在矢状面上的屈曲/伸展活动范围远大于冠状面的内收/外展和横截面上的内旋/外旋活动。 各关节中膝关节的屈曲/伸展活动范围仍是最大的，平均值约为64°。 相比于平地行走，坡地行走时髋关节的屈曲/伸展运动范围显著增加，常规重力下达到50°以上。 同时，各重力水平下踝关节背屈/跖屈活动范围均大于平地行走时的相应值。 因此，坡地行走对踝关节的屈伸活动性要求更高。

图6 坡地行走(3.6 km/h)时髋、膝、踝关节活动范围Fig.6 The range of motion in hip， knee and ankle joints during 15° slope walking(v=3.6 km/h)

坡地行走时，重力水平对髋关节和膝关节的活动范围有显著影响，模拟低重力条件下，髋关节在各个平面上的活动范围均明显减小(屈曲/伸展P＜0.001、内收/外展P＜0.005、内旋/外旋P＜0.05)，膝关节屈曲/伸展活动范围减小(P ＜0.005)。 重力水平对踝关节关节活动范围有较大影响，模拟低重力条件下，踝关节背屈/跖屈和内/外旋活动范围有所增大，内/外翻活动范围略有减小。

3.2 矢状面关节角度变化

3 种步态运动的步态周期均定义为从足跟着地到同侧腿足跟再次着地的过程，一个步态周期可划分为2 个相位：支撑时相和摆动时相，从足跟着地时刻到足尖离地时刻称为支撑时相，从足尖离地到足跟再次着地称为摆动时相[12]。

3.2.1 平地行走

3 种重力水平下，平地行走时髋、膝、踝关节在矢状面上的活动角度变化如图7 所示，图中横坐标代表1 个步态周期，纵坐标正方向代表髋关节和膝关节屈曲、踝关节背屈。 实线表示各重力水平的测量样本均值，阴影区域表示其标准差。

图7 中重力水平1g 下各关节角度变化曲线，步态周期之初，髋关节屈曲约30°，膝关节屈曲约5°，同时踝关节处于稍微跖屈的位置。 足跟着地后，踝关节通过小幅跖屈运动将参考足平放至地面。 膝关节在支撑相初期表现出10°～15°的额外屈曲，起到震荡吸收和体重被转移到该侧下肢时承受重量的作用[12]，之后开始伸展。 随着身体在该侧支撑足向前移动时，髋关节不断伸展，踝关节持续背屈。 在参考足尖离地前，膝关节在几乎完全伸展后已开始屈曲，同时髋关节伸展至最大角度，踝关节开始跖屈。 进入摆动相后，膝关节进一步屈曲，有助于小腿向前摆动，屈曲至最大角度后再次接近完全伸展。 髋关节开始屈曲，恰好在足跟着地前达到最大屈曲角度，之后开始伸展，为足跟着地和承重做准备。 而踝关节在摆动相阶段再次背屈至中性位，使足尖离地。

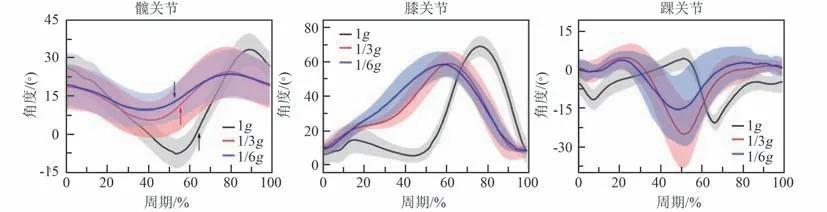
图7 3 种重力水平下平地行走(4 km/h)时矢状面上髋、膝、踝关节角度变化曲线(箭头指示支撑相与摆动相分界点)Fig.7 Hip， knee and ankle joint angles at the sagittal plane during ground walking (v=4 km/h)under different gravity(The arrows indicate the boundaries of stance phase and swing phase)

3.2.2 平地慢跑

3 种重力水平下，平地慢跑时髋、膝、踝关节在矢状面上的活动角度变化如图8 所示。 与平地行走相比，平地慢跑呈现出的特点主要有：

1)在1g、1/3g、1/6g 各重力水平下，平地慢跑时髋关节和膝关节的最大屈曲角度、踝关节的最大背屈和跖屈角度均明显大于该重力水平下平地行走时的相应值；

2)支撑时相变短，摆动时相变长。 平地慢跑时步态周期内脚尖离地的时刻大大提前；

3)1g 水平下，支撑相初期，膝关节额外的屈曲角度明显增大，曲线呈现“双峰”，这是由于慢跑中重心震荡加剧，脚跟着地后，膝关节需要以更大程度的屈曲来缓冲震荡、平稳重心。

图8 3 种重力水平下平地慢跑(7 km/h)时矢状面上髋、膝、踝关节角度变化曲线(箭头指示支撑相与摆动相分界点)Fig.8 Hip， knee and ankle joint angles at the sagittal plane during ground jogging (v=7 km/h)under different gravity(The arrows indicate the boundaries of stance phase and swing phase)

文献中关于行走和慢跑步态的研究报道与本实验结果一致，Novacheck[13]曾报道正常行走时膝关节最大屈曲约为60°，而跑步时增大至90°左右。 唐刚[14]对40 位志愿者的运动测量发现，行走时支撑相在1 个完整步态周期中占据比例大于50%，而跑步时支撑相一般小于50%，即趾尖离地发生在整个周期的50%之前，与行走不同，整个周期中不存在双足着地期，而在1 个周期中将有2 次双足腾空的阶段。 王劲松等[15]通过对不同步速下人体步态规律的测量与研究，得到了人体在跑步机上不同步速行走时下肢关节运动轨迹和关节角度，结果表明支撑相在步态周期中所占的比例随着步速的提高而减小。

3.2.3 坡地行走

3 种重力水平下，坡地行走时下肢髋、膝、踝关节在矢状面上的活动角度变化如图9 所示。 与平地行走相比，坡地行走呈现出的特点主要有：

1)在1g、1/3g、1/6g 各重力水平下，坡地行走时髋关节最大屈曲角度、踝关节的最大背屈、最大跖屈角度均明显大于该重力水平下平地行走时的相应值，膝关节的最大屈曲/伸展角度变化不大；

2)支撑时相变短，摆动时相变长，但变化程度小于平地慢跑；

3)1g 水平下，支撑相之初，髋关节和膝关节的初始屈曲角度增大，而后两者逐渐伸展，并依次伸展至其最大角度，但伸展程度小于平地行走。同样地，摆动相末期，髋关节和膝关节的最终伸展角度也明显增大，但低重力水平会使得2 种运动间的差异减小；

4)足跟着地后，踝关节直接开始背屈，支撑相初期踝关节小幅跖屈运动消失了，这是由于参考足不需踝关节跖屈便可接触带有坡度的地面。

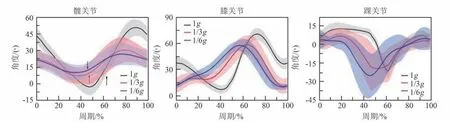
图9 3 种重力水平下坡地行走(3.6 km/h)时矢状面上髋、膝、踝关节角度变化曲线(箭头指示支撑相与摆动相分界点)Fig.9 Hip， knee and ankle joint angles at the sagittal plane during 15° slope walking (v =3.6 km/h)under different gravity(The arrows indicate the boundaries of stance phase and swing phase)

本研究得出的结论与文献中关于坡地行走的研究结果相吻合。 张瑞红等[16]对不同路况下正常步态特征进行了研究，相比与平地行走和上楼梯，上坡行走时的支撑期在步态周期中所占的比例最小(58%)。 唐刚等[17]发现路面坡度对髋关节、膝关节和踝关节矢状面上关节角度均产生较大影响，髋关节的屈曲角和伸展角均随路面坡度的增大而增大，膝关节的初始屈曲角随路面坡度的增大而明显增大，但在步态周期50%～100% 阶段，膝关节在矢状面的关节角度变化受路面坡度的影响不大，踝关背屈角度随路面坡度的增大而明显增大。

3.2.4 重力水平

重力水平对平地与坡地行走和慢跑时下肢关节在矢状面上活动角度的影响如图4～9 所示，模拟低重力条件下的步态运动特征主要表现在：

1)髋关节和膝关节最大屈曲/伸展角度均显著减小，对应各角度曲线的峰值减小或增大，踝关节活动角度随重力水平的降低无显著变化规律；

2)步态时序发生变化，支撑时相变短，摆动时相变长。 以髋关节为例，在足尖离地之前达到最大的伸展角度，随着重力水平降低，髋关节达到最大伸展角度的时刻发生前移，提前进入摆动相；

3)曲线变得更加平滑，峰值不再尖锐，这表明低重力水平下，各关节在屈伸到最大角度后将作短暂停留，也可以说，关节活动由屈曲变为伸展的动作在步态周期内所占据的时间比例被拉长了，步态动作更加缓慢。 值得注意的是，坡地行走中，足尖离地后踝关节达到最大跖屈角度后持续了更长的时间，在步态周期内所占的时间比例明显增大；

4)膝关节和踝关节的缓冲作用减弱，低重力条件下，支撑相初期膝关节额外的屈曲峰几乎消失，踝关节背屈的时间比例缩短，这是由于重力水平的降低使得重心震荡带来的载荷冲击减小，因此下肢关节的缓冲策略也相应减弱。 这一特性在平地行走和平地慢跑中表现得较为突出；

5)步态周期内足跟离地提前，呈现“跳跃型”步态。 以平地行走为例，如图7 所示，正常重力水平下，踝关节持续背屈，到支撑相后期，足跟离地之后踝关节开始跖屈，并在足尖离地后达到最大跖屈(15°～20°)，模拟低重力条件下，踝关节在支撑相的背屈时间缩短，足跟过早离地，呈现“跳跃型”步态，这表明低重力水平下更倾向于采用一种行走-蹦跳的步态策略；

6)低重力条件下方差带变宽，这表明个体差异比较明显，不同受试者对低重力环境的适应和在低重力环境中采取的步态策略有较大差异。

3.3 航天服下肢关节配置

基于本研究的测试数据，梳理出了满足平地与坡地行走和慢跑需求的下肢关节活动范围，为星际航天服下肢活动性指标的确立提供参考，如表1 所示。

测试结果表明，不同重力水平下，行走和慢跑中下肢各关节均以矢状面的屈伸运动为主，因此，星际航天服关节在配置时必须首要保证髋关节、膝关节、踝关节屈伸的自由度。 髋关节内收/外展、内旋/外旋的活动范围相比于屈曲/伸展范围较小，但对于实现步态行走也起到重要作用，内收/外展活动自由度可改善航天员的侧向稳定性，内旋/外旋活动自由度可辅助实现行走过程中改变方向的功能，因此，髋关节在实现较大范围屈伸活动的同时，需在另外2 个方向上配置小角度的活动自由度。 膝关节在下肢各关节中活动范围最大，需配置可实现大范围运动的单自由度关节。踝关节在各个方向上的活动范围均处于中等水平，行走过程中，踝关节可以调整足部位置，对于保持侧向平衡来说，甚至很小的踝关节活动角度都非常重要。 在保证屈伸自由度的基础上，另外2 个自由度的活动对于实现坡地行走必不可少，表1 中踝关节内/外翻和内/外旋活动角度的极值均出现在坡地行走中，内翻/外翻活动自由度能够使得航天员在斜坡上或者踩在崎岖的星面上时保持姿态稳定，实现坡地的安全行走；内旋/外旋活动自由度可实现行走时改变方向，躲避障碍物，有利于在不平坦的地形上可以采取最稳定的姿态。因此，星际航天服踝关节在配置和设计时需保证多自由度的活动性。

4 结论

1)不同重力水平下平地行走、平地慢跑和坡地行走时，人体下肢各关节在矢状面上的屈曲/伸展活动范围远大于冠状面的内收/外展和横截面上的内旋/外旋活动，其中，膝关节屈伸活动范围最大，不同步态中均达到60°以上。

2)模拟低重力条件下，髋关节和膝关节在各个平面上的活动范围均明显减小，踝关节活动角度无显著变化规律。

3)重力水平降低后，髋关节和膝关节最大屈曲/伸展角度均显著减小，膝关节和踝关节的缓冲作用减弱；低重力条件下，步态运动的支撑时相变短，摆动时相变长，倾向于采用一种行走-蹦跳的步态策略。

4)基于模拟低重力水平下的运动学特征，梳理出了满足平地与坡地多种步态需求的下肢关节活动范围，为星际航天服下肢活动性指标的确立及关节结构设计提供参考。

参考文献(References)

[1]管春磊，李猛，陈景山.美俄新型登月航天服技术研究进展[J].载人航天，2010， 16(2)：45-51.Guan C L， Li M， Chen J S.Advances in the American/Russian lunar extravehicular space suit [J].Manned Spaceflight，2010， 16(2)：45-51.(in Chinese)

[2]Hill T R， Johnson B J.EVA space suit architecture： Low earth orbit Vs.Moon Vs.Mars[C]/ / IEEE Aerospace Conference， Big Sky， MT， USA： IEEE，2010：1-28.

[3]王世杰， 李雄耀， 唐红， 等.月面环境与月壤特性研究的主要问题探讨[J].地球化学， 2010， 39(1)：73-81.Wang S J， Li X Y， Tang H， et al.Lunar surface environment and properties of lunar soil： A review [J].Geochimica.2010， 39(1)：73-81.(in Chinese)

[4]陈景山， 李潭秋， 边晋梅， 等.航天服工程[M].北京： 国防工业出版社， 2002：181-194.Chen J S， Li T Q， Bian J M， et al.Spacesuit Engineering[M].Beijing：National Defense Industry Press， 2002：181-194.(in Chinese)

[5]Schmidt， Barrett P.An Investigation of Space Suit Mobility with Applications to EVA Operations[D].Massachusetts：Massachusetts Institute of Technology， 2001.

[6]Jacobs S， Tufts D.Space suit development for the multi-purpose crew vehicle[C]/ /42ndInternational Conference on Environmental System.San Diego， California： AIAA， 2012：3550.

[7]Ackermann M， Van den Bogert A J.Predictive simulation of gait at low gravity reveals skipping as the preferred locomotion strategy[J].Journal of Biomechanics， 2012， 5(7)：1293-1298.

[8]Ackermann M， Van den Bogert A J.Optimality principles for model-based prediction of human gait[J].Journal of Biomechanics， 2010， 43(6)：1055-1060.

[9]Minetti A E， Alexander R M.A theory of metabolic costs for bipedal gaits[J].Journal of Theoretical Biology， 1997， 186(4)：467-476.

[10]Minetti A E， Alexander R M.Biomechanics： walking on the other planets[J].Nature， 2001， 409(6819)：467-469.

[11]王成焘， 王冬梅， 白雪岭， 等.人体骨肌系统生物力学[M].北京：科学出版社， 2015：5-8，71-74.Wang C T，Wang D M，Bai X L，et al.Human Musculoskeletal System Biomechanics [M].Beijing：Science Press， 2015：5-8，71-74.(in Chinese)

[12]Neumann D A.Kinesiology of the Musculoskeletal System Foundation for Rehabilitation [M].Singapore： Elsevier，2014：638-644.

[13]Novacheck T.The biomechanics of running[J].Gait ＆ Posture， 1998， 7(1)：77-95.

[14]唐刚.人体典型运动生物力学仿真分析[D].上海：上海交通大学， 2011.Tang G.Biomechanics Simulation Analysis for Typical Movements of Human[D].Shanghai：Shanghai Jiao Tong University， 2011.(in Chinese)

[15]王劲松， 王令军， 王婷， 等.不同步速下人体步态规律的测量与研究[J].传感器与微系统， 2008， 27 (9)： 43-45.Wang J S， Wang L J， Wang T， et al.Measurement and study of the human gait law at asynchronous speed[J].Transducer and Microsystem Technologies， 2008， 27(9)：43-45.(in Chinese)

[16]张瑞红， 金德闻.不同路况下正常步态特征研究[J].清华大学学报：自然科学版， 2000， 40(8)：77-80.Zhang R H，Jin D W.Normal gait patterns on different terrain[J].Journal of Tsinghua University： Sci＆ Tech， 2000， 40(8)： 77-80.(in Chinese)

[17]唐刚， 张希安， 季文婷， 等.坡面步行中青年女性下肢关节角及肌肉激活度[J].医用生物力学， 2011， 26(2)：158-192.Tang G， Zhang X A， Ji W T， et al.Joint angles and muscle activations in the lower limb of young women during slope walking[J].Journal of Medical Biomechanics，2011， 26(2)：158-192.(in Chinese)