从粒子性角度论述热力学问题

摘 要：从粒子性角度描述热运动及其热传递，形式上可简化为粒子的运动和自转性能的相互转化，热传递可简化为粒子之间的双重运动性质的交换，即动能交换及自转能的相互转化。能量的守恒也可以等效为粒子的动能和自转能之间的守恒问题来描述。所以，所谓的热交换是相互的。热传递具有相互性。

关键词：热运动 热交换 动量交换 相互性 温度 熵

稳态熵轨道

引 言

本文从粒子性角度论述了物体的热运动以及物体之间的热传递规律，理论表明，热运动微粒子在双重运动中的相互作用。相互作用可以用动能的相互碰撞形成的相互作用以及自转导致的摩擦而形成的相互作用来描述。系统中粒子之间的相互作用力的大小表现为对外界的温度的高低。温度的高低变现为系统的熵的高低。所以从粒子性角度描述热运动及其热交换时，热交换具有相互性。熵曾和熵减都是属于自然演变。

一、从粒子性角度论述热运动规律

粒子稳态：是指一个微粒子在不受任何其它影响的前提下，粒子具有自由运动状态，自由运动状态表现为粒子的自转及其在自转形成的内力作用下的环绕运动。所以，粒子的稳态可理解为粒子的自由绕动状态。

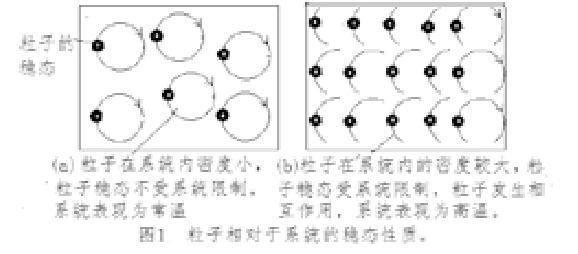
系统的相对性稳态：一个系统的体积不小于系统内所有粒子的二维运动（绕动所体现的扁球体的体积）的球体体积时，可视为粒子之间及对系统无相互作用，可视为系统处于相对性稳态性质。如图1（a）。

热运动：一个相对封闭系统内，由于粒子数量增多，粒子不能在稳态中运动，粒子之间会发生碰撞，在碰撞相互作用中，粒子运动速度加快，自转能的减小不能及时的等量抵消动能的增大，表现为热运动。热运动对系统产生压力，压力的大小表现为系统的热量（温度）大小，如图1（b）。

当一个稳态系统内粒子的稳态受到外界的影响而增大粒子的二维运动体积后，相对系统体积不变时密度增大，大于系统体积时也会显示为热运动状態。热运动状态是相对的。

二、从粒子性角度描述热传递现象

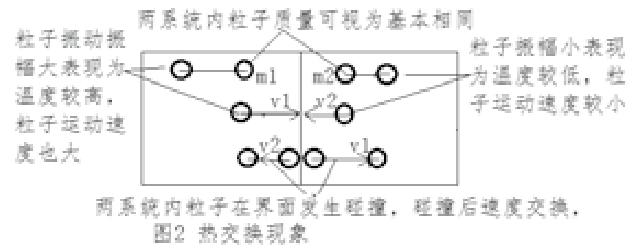
（一）动量交换。粒子的绕动可简化为振动。粒子的相互作用可用动量定理来来描述。两个系统温度不同相互热传递时，可视为两个系统内粒子在碰撞中导致的动量交换。如图2。

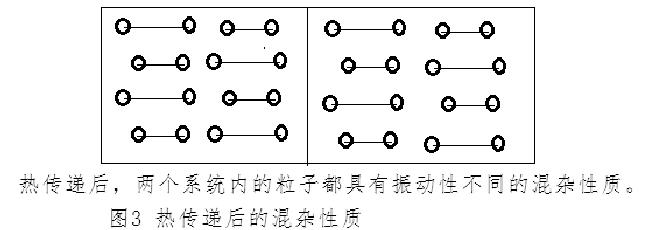
两系统内粒子视为质量m1和m2相同，温度高的左边内粒子振动振幅较大，粒子运动速度v1也较大。右边粒子振动振幅较小，粒子运动速度v2较小。系统热传递可视为粒子在界面发生碰撞的相互作用。根据动量守恒定律。碰撞后两个系统内粒子运动速交换，等效为为热交换。可简单理解为，两个系统内的粒子在平衡后温度相同，但属于震动振幅不同的粒子的均匀性混杂性质，如图3。

但从动量守恒的原理上分析，热传递可视粒子动量交换，可视为热交换。而且具有粒子动量不同的混杂性质。

（二）自转能能对动量交换的影响。根据《自由运动论》所描述的能量守恒定律，粒子具有运动和自转的双重运动性。而且总能量是不变的。所以，系统内相同粒子动能（动量）较大的，自转能必定较小，自转速度较小。由图2所描述的动能较大的粒子的自转能较小，自转速度必定较小。动能较大的粒子的自转速度较大。如图4。

在部分相互碰撞形式的相互作用时，粒子会因为自转导致碰撞点处具有摩擦力，且摩擦力使自转速度大的减小，而有利于自转速度小的增大。m1的运动速度V1较大，m2的运动速度V2较小。在摩擦力f作用下，摩擦力对于动能较小的m2的自转速度w2的影响较较大。碰撞后的自转速度w4减小幅度较大。而有利于m1粒子的自转速w1的增加。也就是说，在相互作用中，自转速度不是互换的，是受不同影响的。根据能量守恒，相互作用后的运动速也并非是互换的了，即同时考虑自转在碰撞中的影响及其变化，动量不守恒。但是，在多次的碰撞中，自转速度w3和w4接近相等，运动速度v1也接近v2也会接近相等。两系统内的粒子从图3显示的振动性质不同的混杂性质变为振动性能基本相同的性质。

由以上分析，热传递从粒子的动量守恒及其能量守恒的角度分析，热传递具有能量互换性质。

三、热力的应用

（一）热力的实质。所谓热力，是利用能源从低温到高温的体积变化来产生对外压力。比如，汽油在气缸内燃烧，实际上可等效为利用汽油和空气的的反应，使体积小的液体汽油变为体积大的气体物质的过程。对活塞产生向外的压力从而获得动力。

所谓的燃烧，可等效为让体积较小的物质（液态）内的复粒子在湮灭性质的碰撞之后，重组为体积更大（气态）物质的复粒子的过程。

（二）现代热力学的局限性。所谓的热力，是指系统相对高温物质会对系统外部产生压力。技术上可以利用相对低温自然能源（比如煤炭、汽油燃烧等）来人为制造高温能源，再利用这一高温压力的释放来获取动力。而且类似煤炭低温能源体积小容易携带。

但是，气态到液态变化，虽然理论上存在反向压力，但技术上用自然气态能源来人为的转化为液态的过程是比较困难的。比如，如果把容易起化合反应的某些气体混合，可以生成液态或者固态物质，理论上也是可行的。相当于密度较小体积大的气体在气缸内结合生成密度较大体积较小的液态或者固态物质，从而使气缸内压力减小，使活塞获得外界空气压力，从而获得活塞向内运动的动力。但是，如果利用此反过程来获得动力，会存在气体能源体积大不易携带，而且气缸也不宜太大的弊端。

所以，理论上，动力能源是可以利用热力的反过程来实现的。即热力也已利用物质从高温（气态）到低温（固液态）的自然过程（化合反应）来获取动力的。只是反过程不利于机械的设计及利用。

实际上，利用高温的膨胀力的过程本来是人为的把低温（汽油等）通过反应（燃烧），变成气体物质，才导致高温气体看起来自动向外部低温空气传递（产生压力）的性质。也就是说，物质从高温向低温自动传递性，是源于前期低温向高温自动变化的过程。也就是说，理论上，利用物质从低温到高温的交换过程，从高温到低温的交换过程都可以对外做功而获得动力的。

四、能量、温度及密度的关系

依据《自由运动论》的理论，光粒子的质量是不尽相同的，在不尽相同的碰撞中形成的复粒子的性质也就不尽相同。从复粒子的不同性质来分析，复粒子的自转能越大，体积越小，形成的宏观物质密度也大。也就是说，同样的粒子，构成密度大的物质时，粒子的能量储存在自转能中的能量较大。相当于，密度越大，能量越大。虽然密度大，是由于粒子的自转速度大导致的粒子稳态体积小，相互之间的作用力不会因为密度大而增大。所以，自然条件下，密度大不代表温度就高。

密度大不代表温度就高，是指物体质量较小，不考虑物体内部粒子和外部粒子的区域性差别。但是在形成庞大天体的情况下，由于粒子数量巨大。所谓物体具有内外的绝对性区别。在自由运动中形成相对封闭区域，粒子会因为空间的局限而被迫增大密度，会形成局部密度越大，温度越高的现象。此时情况就不属于自由状态下的密度。意味着，质量较大的物体内部物质温度随着区域性变化而变化。比如，地球大气层，本来属于同类粒子构成的气体物质，温度、密度本应相同，但由于大气分子数量巨大，形成各自的自由运动受到局限，产生挤压，形成内部压力增大，密度增大，从而温度升高，形成大气层温度具有向外逐渐减小的大的规律。

五、熵的物理意义

关于熵的现代物理学等意义大致可理解为，一个系统中的物质内所有粒子越是具有自由性，系统变现为越混乱，混乱程度越大，系统的熵值越大。越混乱粒子显得越是无序，即也可认为，系统越是无序，熵值越大。反之，熵值越小。如图1（a）中的粒子数少，在自由的运动中位置是多变的，显得无序，而粒子的三自由度也较大，即粒子的自转和绕动方向也是很大程度的不一致。而在图1（b）中，由于粒子数量居多，在相互作用中，自由运动范围较小，位置不能较大幅度的移动，显得更有序，而且三自由度受限制，绕动方向也更具有一致性。所有粒子表现为较为有序性质。

从熵的广义性角度来考虑，就是从宇宙大尺度范围内，一个天体的熵值也是如此。天体的密度越小，单位体积内的微粒子数越少，粒子间相互作用力越是小，粒子越是自由，天体的熵值越大。而有些天体的密度较大，熵值就叫小。天体的旋转速度越大，密度越大，内部粒子越有序，也表现在粒子的自转方向越一致，天体的扁球体性质的扁率越大。所以天体（或者星系）越是扁平熵值越小，自转速度越小，越是接近正球形，熵值越大。

系统内所有粒子在自然条件下向着自由无序方向自动演变，而不会向着反方向自动演变，是热力学第二定律的意义。比如，一个系统，压力越大，系统内粒子越是不自由，也是越是在压力下变得更有序。而压力越大，粒子之间的相互作用力越大，动能变得越大，对外显示为温度越高。所以，在两个不同温度系统之间相互交换热量的过程中，总表现为：

1.温度较高的有序系统内的粒子自动向着温度低的无序系统内传到动能，如图2所示，两个系统是隔离的，粒子不能到达对方的空间中去。

2.温度较高的有序系统内的粒子自动向着温度低的无序系统内运动，然后两个系统内的粒子混合到均匀分布（如图3不存在系统隔离层的整体均匀情况）。也就是说，热传递是有方向的，其方向性就是所谓的熵曾原理。即系统熵会自动增加，不会自动减小。

六、稳态熵轨道

（一）稳态熵的定义。用熵来描述物质的属性是可以的，但是根据《自由运动论》的理论，熵可以延伸到宇宙空间中。一个天体，一个星系，都可以用熵来描述。比如地球，地球可以理想的理解为由某些空间粒子连续的发生纠缠性质的碰撞而逐渐形成的。可认为这些粒子是从熵值很大的自由状态中自然演变为熵值很小的，密度很大的天体。

当同类粒子构成一个系统，系统空间不小于所有粒子的稳态体积的和时，粒子之间基本可以处于自由运动状态，系统熵可视为稳态熵。粒子在自由的稳态熵性质中做更高维度的轨道运动，其轨道可视为稳态熵轨道。

每类粒子都有自己的稳态二维体积及其相对的更高维度运动轨道，比如大气分子，有一定的稳态体积，也有随着地球自转而绕地球运动稳态轨道。如图5。

设：空气的稳态轨道处的熵值为稳态熵值，则稳态轨道外围空气的熵值较大，稳态轨道内的空气的熵值较小。同类的空气分子，处在稳态轨道外的熵值较大空气有自动向着稳态运动的趋势。而低处的熵值较小的空气有向着熵值较大稳态轨道上运动的趋势。由于同类粒子居多，某系统的稳态熵轨道上的熵值并不是稳态熵值，而是小于稳态熵值。

（二）稳态熵轨道的多维性。和粒子的双重运动性具有多维性一样，稳态熵轨道也具有多维性。比如，一个电子在原子中的稳态熵轨道为一维稳态熵轨道，原子在分子中的稳态熵轨道就属于电子的二维稳态熵轨道，分子在更大的系统内的稳态熵轨道属于电子的三维稳态熵轨道。

整个太阳系中，天体也具有特定的稳态熵轨道。在中途没有发生碰撞的光粒子会到达大尺度范围上的绕太阳公转，可认为此处的光粒子是自由的，因而，可以认为光在空间中辐射以及公转区域属于熵值最大的物质区域 ，可视为光粒子的稳态熵轨道。

质量巨大的天体在纠缠性碰撞中质量增大，熵值向着减小的方向演变，在湮灭性碰撞中向着熵值减小的方向演变，都具有向着各自的稳态熵轨道上演变的性质。即，天体的稳态熵轨道，可视为微粒子的更高维度的稳态熵轨道。

（三） 稳态熵轨道的物理性。由以上分析可知，密度越小的同类粒子形成的系统内，由于压力而存在的不同温差（能量差）越小，表现为密度越小的系统能量分布越接近均匀，比如同等范围内，气态层的温差要小于液态层的温差，液态层的温差要小于固态层的温差。即，整体性质表明，密度也小，熵值越大。

每种不同物质构成的系统都存在一定的运动曲率轨道。表明，物质的熵和物质的双重运动性有关，与物质的运动曲率有关，而且有运动曲率越小，密度越小，物质内（系统内）粒子越是显得自由，熵值越大。说明，熵值与系统运动自由运动曲率成反比。

（四） 熵变的可逆性。天体的形成可以理想的视为最自由的微粒子的纠缠性碰撞而逐渐形成的。而其过程也属于自由运动中的演变过程，其过程可视为粒子的熵是从大向小的方向自由演变。比如类星体、黑洞等是天体之间的很大程度纠缠性碰撞，所以类星体等属于自转速度逐渐增大，在惯性作用下吸收空间粒子的能力较大。于是有质量逐渐增大、密度逐渐增大的性质，从而表现为熵值逐渐减小的性质。从广义上考虑，结合稳态熵的性质，自然条件下，宏观物体的形成，直至质量巨大的天体的壮大过程，就是熵减的过程。熵减也是属于自由演变的性质。只能说，熵曾原理是在特定前提下或者局域条件下建立的物理规律。

七、结论

热传递过程，可理解为粒子在相互作用中动能和自转能的相互交换过程，从能量守恒性质上考虑，热传递具有相互性。系统能量不存在绝对的能量均匀分布，总存在能量差，表现为，密度越小，能量差越小，熵越大。系统的熵都具有稳态熵区域，系统粒子都有向着稳态熵区域运动的趋势。从粒子相互作用的多样性来考虑，粒子的纠缠性碰撞形成复粒子的自然过程是系统的熵减的过程。湮灭性碰撞的自然过程是系统的熵增过程。所以，自然规律中，某系统在演变中既可以自动熵曾，也可以自动熵减。所以，现代物理学所描述的热力学第二定律以及熵增定律具有狭义性，或者说是不符合自然规律的。

参考文献

[1] 咸立德.《自由运动论》[c]全国智慧城市建设应用高峰论坛论文集2016.

[2] 咸立德.从粒子性角度论述微粒子纠缠現象的成因——《自由运动论》在实际中的应用（27）[J]新产经2016（11）。

[3] 咸立德.微粒子在碰撞中形成湮灭现象的成因——《自由运动论》在实际中的应用（28）[J]新产经2016（11）。