探究一道题的多种解法
2019-07-01张波
张 波
(黑龙江省哈尔滨市第一二二中学 150040)
题目设x、y是实数,且x2+xy+y2=1,求p=-x2+xy-y2的取值范围.



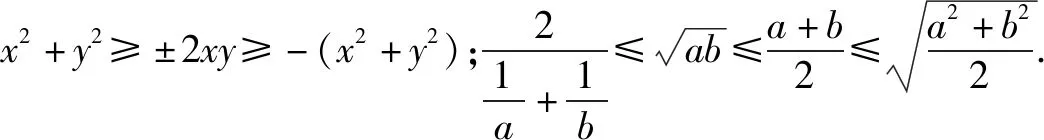

由条件x2+xy+y2=1知x与y不能同时为零.
(1)当x与y中有一个为零,另一个不为零时,显然p=-1.

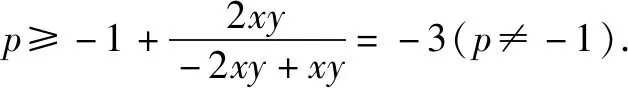

点评本解法的关节点是对x与y符号的讨论,这是因为x2+y2≥2xy取等号与x2+y2≥-2xy取等号时,x与y的符号条件不一样.
解法3(判别式法)由
x2+xy+y2=1⟹p(x2+xy+y2)=p=-x2+xy-y2⟹(p+1)x2+(p-1)xy+(p+1)y2=0.

(1)当p+1=0,即p=-1时,x=0,y=±1,符合题意.


点评本解法中要注意两个易错点:①讨论后明确了y≠0,才能化得方程(*);②对方程(*)应用判别式的前提是一元二次方程,因此要考虑二次项系数p+1是否为零.



点评本解法逆用韦达定理,根据导出的x+y,xy的表达式构造出一元二次方程,再利用判别式轻松获解.但应注意解题中隐含条件p≥-3,才能使解题过程严谨无误.
解法5(利用非负数)
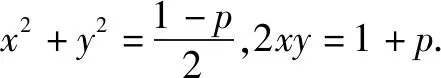
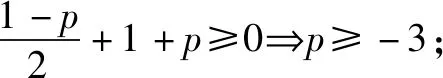

点评本解法中要注意构造非负数的两种形式,若只考虑到非负数的一种形式,将导致以偏概全的错误产生.
解法6(引入等差数列)
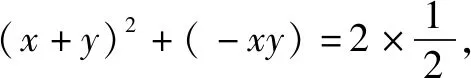


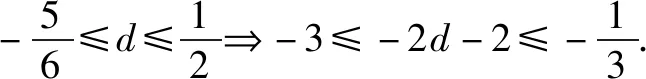

点评本解法中引入了公差d,从而简化了p的表达式,只需确定d的取值范围,就可获得答案.
解法7(施行三角代换)
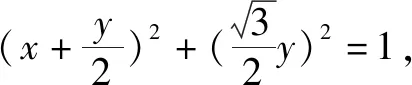


点评本解法思路常规,做出的三角代换也很自然,但三角运算较复杂,需要具有一定的三角变换功底.
解法8(利用齐次分式)
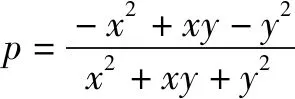
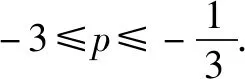
点评对于二次齐次型的分式,都可以用上述方法化为三角分式的形式,特别当x2与y2的系数相同时,所化得的式子更为简单.
在进行高考数学专题复习时,为避免题海战术,教师应选择典型题目,进行一题多解的深入探究,鼓励学生广开思路,不断挖掘,就会探索出多种新颖而富于创造性的解题思路.这对于活跃课堂教学氛围,开发学生智力,提高复习效果大为有益.这完全符合新课标所倡导的提升学生素养、培养创新型人才的教学理念.
