导数在高中数学解题中的应用探析
2019-07-01周晓
周 晓
(福建省霞浦第一中学 355199)
作为微积分中的基础知识,导数在研究函数问题和解决实际高中数学难题中发挥着不可忽视的作用.导数通过将函数、方程、向量、数列、不等式、解析几何等内容有机联系起来,并为解决这些问题提供了较为统一且能让学生容易理解和上手的学习方法.根据笔者多年实践和观察发现,伴随着高中新课程改革的不断深入,导数在高中数学解题方面的作用越来越明显,地位也越来越特殊,深受学生喜爱.当前,高考考查导数知识角度很多,但万变不离其宗的是导数与其他数学知识综合应用能力.比如,导数在解决函数、不等式、切线等实际数学问题中的应用,这不仅要求学生牢牢掌握与导数相关的基础知识,而且还能够学以致用,将其运用到解题过程中去.笔者认为,在日常教学活动中,尤其是备考阶段,数学教师要帮助学生巩固导数相关知识,通过模拟练习培养和不断提高学生利用导数解决实际问题的综合能力.
一、导数在判断函数单调性过程中的广泛应用
众所周知,函数的单调性是高中数学的主要知识点之一.所谓函数的单调性,指的是在某一区间范围内,由于自变量发生变化,随之因变量也会发生变化.一般情况下,判断函数单调性的依据,我们率先想到的是其具体定义.也就是说,在某一区间范围内,倘若函数中自变量变大,而因变量随之变小,则我们称之为减函数;而倘若函数中自变量变大,因变量也随之变大,则我们称之为增函数.其中,相应的区间是其与之对应的单调区间.多年实践和教学心得发现,这一判断方式较为满足且适用于相对简单的函数单调性.但是,当面临稍稍复杂的函数时,这一解题思路则会变得显得过于复杂,同时证明起来相对不易.近年来,伴随着导数的出现及其在高中数学中的广泛应用,判断函数的单调性也变得相对容易起来,不仅快速而且可靠度高,学生也易掌握.通过导数具体判断某一函数的单调性时,一般做法如下:首先,进行函数在区间范围内的求导.倘若求导结果>0,那么可以说明的是,此函数在这一区间范围内,单调呈递增性质;倘若求导结果<0,则此函数在这一区间范围内,单调呈递减性质.笔者认为,若要快速且准确地判断函数单调性,至关重要的一点是熟练掌握一般函数的求导方式.此外,还要对函数的单调性和函数所对应的区间进行说明.
二、导数在证明不等式过程中的广泛应用
纵观近年来高考数学考查内容,笔者发现,考题综合化及知识的灵活应用成了现阶段及未来一段时间内高考命题主要发展趋势之一.而针对高中数学而言,把不等式相关问题与函数结合起来综合考查,则成了最为普遍的命题形式之一,很受欢迎.在证明不等式过程中,充分运用导数效果十分明显,不仅让考官和教师一目了然,而且相较于以前的解题方式,利用导数解题速度得到了大大的提升.导数在证明不等式过程中的应用一般做法是:将要证明的不等式进行变形,使其变为判断两个函数大小的题目;接着构建辅助函数、求出具体导数值;然后再对导数在区间上的正负情况进行判断,确定其单调性;最后判断这两个函数的大小值.此处要引起注意的是,在证明指数函数、对数函数以及三角函数的过程中,通过导数一方面可以有效提高解题的速度,另一方面还能够引导学生深层次地掌握不等式、方程以及函数等相关知识及其之间的关系,从而加深对其的印象和理解.

证明设AB的中点是P(m,n),那么中点P在椭圆内.
因此,-a 因此,线段AB的垂直平分线斜率满足: 一直以来,一提及函数求解最值,人们往往会叹而止步,因为其往往是作为高考难点而出现在考生眼前.针对函数求解最值这一知识点,求解方式可以说是千姿百态.以往的求解方式可以满足一般函数,但是碰到求解较为复杂的函数最值的时候,考生往往会显得无从下手,甚至不知所措.此外,更为头脑的是其解题过程相对不简单.而导数的出现则大大化解了这一尴尬.举个例子,我们常见的二次函数求解最值.难点在于,因为二次函数所需要求解的最值是在某一区间范围的最值,这就要求分别求出这一区间范围内的最大值抑或是最小值.过去我们遇到这个问题,往往会采取数形互相结合这一方式,而这对于学生而言,解题过程显得较为繁复冗长,时间成本较大.而通过导数则显得较为简单、快捷,一般做法是:通过导数判断出该函数在区间范围内的单调性和最大值、最小值,然后对其最值与区间对应关系进行明确,可以说是既高效又快速. 分析第一步:求出f(x)的极值点; 第二步:对比极值点与区间端点函数值; 第三步:求出该函数在区间范围内的最大值、最小值. 解因为f′(x)=3x2-3=3(x2-1)=3(x+1)(x-1),则 当x∈[-3,-1]或者x∈[1,3/2]时,f′(x)>0,因此[-3,-1],[1,3/2],则是该函数的单调增区间; 当x∈[-1,1]时,f′(x)<0,因此,[-1,1],则是该函数的单调减区间. 由于f(-3)=-18,f(-1)=2,f(1)=-2,f(3/2)=-9/8. 因此,当x=-3的时候,f(x)的最小值为-18; 当x=-1的时候,f(x)的最大值为2. 总的来说,导数在高中数学应用十分广泛,不仅仅局限于上述所呈现的几种,方便学生答题解题的同时还在无形中大大提高了对学生的要求.由于导数相关知识点的学习安排在教材末尾,因此在实际解题过程中,学生往往会通过自己惯用的思维来答题,对导数的应用不多.笔者认为,在日常模拟考试及学习过程中,高中数学教师可以适当增加导数相关内容,拓展学生解题思维,提高解题能力.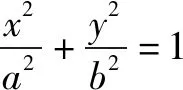
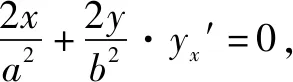
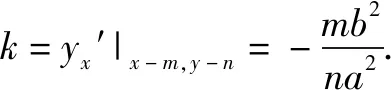


三、导数在求解函数最值过程中的广泛应用

