“一题四解”培养多角度思考能力——以2018年江苏省对口单招高考数学一道压轴题为例

戴志强

(江苏省常熟高新园中等专业学校 215500)

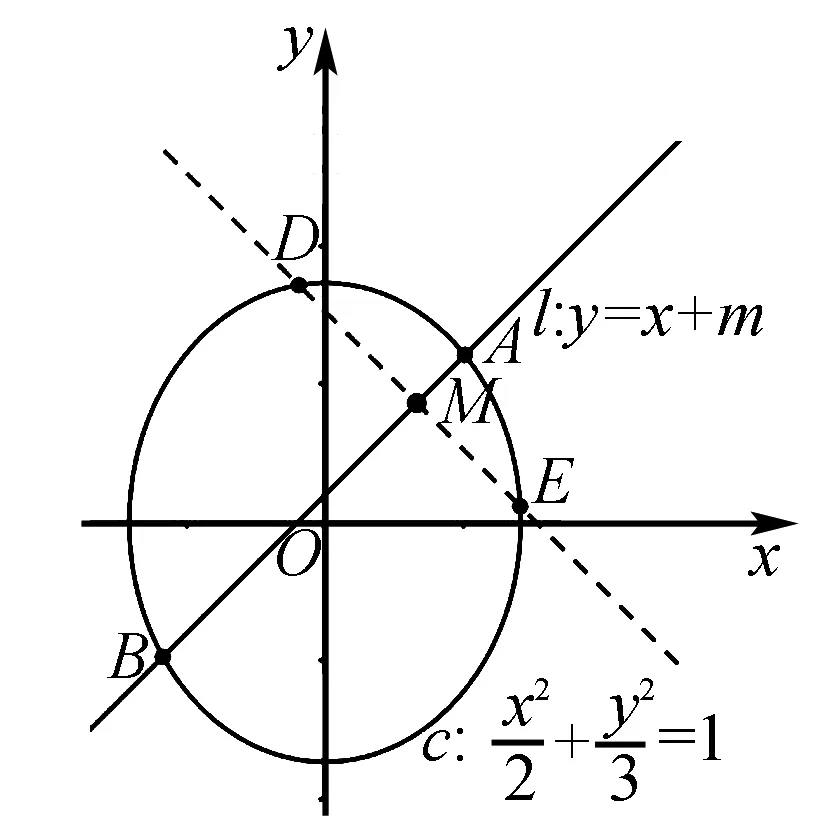
本文以2018年江苏省对口单招高考数学试题第23题的第(3)小题为例进行分析.

一、从中点弦的点差法角度思考解法

解法思路分析：中点弦的“点差法”是圆锥曲线题型的一类常用解题方法，是一种常见的思考角度.在本题中，在椭圆内部作直线AB的垂线DE，由题目提供的对称性条件可推出涉及弦DE的中点坐标，因此可以将直线与圆锥曲线相交的两个交点代入曲线方程，再将两个方程作差，求出直线的斜率，进而求出弦DE的中点坐标，最后根据中点坐标必须在椭圆内这个限制条件可解出答案.

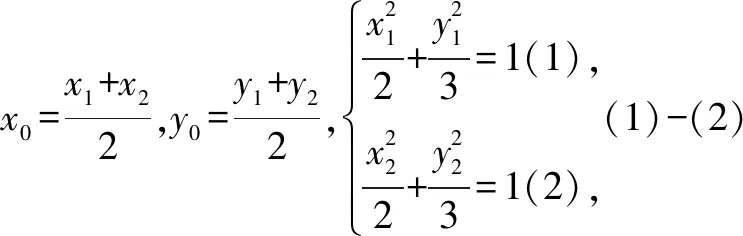
二、从对称性蕴含的约束条件角度思考解法

解法思路分析： 本题的核心在于理解题中的“对称”这个条件，从对称性角度去思考，可以得出其蕴含的约束条件是：垂直与平分，即直线AB是弦DE的垂直平分线.这是一个可行的解题思考角度，从满足约束条件入手可顺利解题.

三、从点形成的轨迹角度思考解法

解法思路分析：因为椭圆内部满足题意条件的弦有无数条，所以所有平行于DE的弦的中点形成轨迹，从点形成的轨迹角度思考，结合轨迹与椭圆的位置关系，可求出变量m的范围.

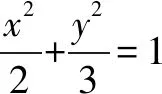
四、从二次函数根的分布角度思考解法

解法思路分析：由题意可知椭圆c上被直线AB(即直线l)垂直平分的弦DE存在，从而可推导出弦DE所在的直线与椭圆c存在两个不同的交点，即直线DE的方程与椭圆c的方程组成的方程组存在两个不同的解.由方程组可得到一个二次函数，从而将本题的几何问题转化为函数问题，即考察二次函数在某段区间上根的分布条件.