粒子群算法在机械手臂B样条曲线轨迹规划中的应用

郭彤颖，刘 雍，王海忱，李 峰

(沈阳建筑大学 信息与控制工程学院，沈阳 110168)

0 引言

机械手臂作为自动化设备中的一个重要组成部分，以其操作灵活性，被广泛应用于工业生产、医疗服务、军事科技等各个方面。对于不同的工作环境，我们要对机械手臂的各个关节进行具体的轨迹规划，从而得到机械手臂末端的位姿，因此，对机械手臂进行精确快速的轨迹规划就显得尤为重要[1]。机械手臂关节空间的轨迹跟踪就是通过控制各关节的位置、速度、加速度等变量使机械手臂沿期望轨迹运动[2]。

早在1971年Kahn和Roth[3]就研究过在做假设和近似的前提下，机械手臂做点对点运动时的最优轨迹问题。Bazaz和Tondu[4]利用三次样条函数进行在线轨迹规划，并进行了时间最优化的设计，其缺点为不能使轨迹点间的加速度连续。Piazzi A和Visioli A[5]设计了时间最短条件下的三次样条轨迹规划，其由5段三次多项式插值满足位置、速度、加速度的约束条件，但是缺点是不能满足脉动连续。恽为民[6]利用遗传算法优化机械手臂的动力学模型，设计了机械手臂的最优时间轨迹规划，缺点是多自由度计算时速度较慢。李俊等[7]以多关节机器人为对象，利用样条函数和改进的遗传算法，避免了运动轨迹出现奇异结构点和局部最优问题，但缺点是结果可靠性差，不能稳定求解。管成等[8]提出了一种基于NURBS曲线的轨迹规划方法，能够得到满足物理约束的时间最优关节轨迹，缺点是求导计算式繁琐，求解效率低。

本文研究过路径点的基于关节空间的轨迹规划，使轨迹与B样条曲线逼近，并运用粒子群算法进行优化，最终达到的效果是使轨迹更加平滑连续，提高机械手臂的稳定性。

1 基于B样条曲线的轨迹规划

Bezier曲线是由法国工程师皮埃尔·贝塞尔(Pierre Bézier)于1962年提出的一种曲线逼近方法[9]。而B样条曲线则是Bezier曲线的一种一般化，其继承了Bezier曲线的优点并克服了其缺点。四阶三次的B样条曲线的表达式为：

(1)

其中，P0，P1，P2，P3为4个控制节点，0≤u≤1。

应用B样条曲线函数规划机械手臂路径的基本思想如下：以机械手臂的关节空间中每个采样区间端点为型值点，设其为V1，V2，...，Vm，根据连续性条件以及边界条件，可以求出m个控制点P1，P2，...，Pm。则每两个相邻型值点之间可用一段B曲线连接，因此，整个轨迹即为m-1段B曲线拼接而成。设第i段B曲线连接的型值点为Vi和Vi+1，则第i段曲线将由Pi-1，Pi，Pi+1，Pi+2这4个控制节点来控制。控制节点的坐标可表示为Pi-1(ti-1，qi-1)，Pi(ti，qi)，Pi+1(ti+1，qi+1)，Pi+2(ti+2，qi+2)。这样，当路径点确定后，即可通过相邻的4个路径点确定一段完整的B样条曲线路径，并通过Bezier函数确定各个关节的运行情况。若t(u)，q(u)分别表示第i段曲线上任意点的横纵坐标，则机械手臂的B样条曲线方程可表示为：

(2)

(3)

为了得到P1，Pm两个控制点，B样条函数需要附加2个边界条件，即附加两个控制点P0和Pm+1。

约束条件为对公式(1)进行一阶求导和二阶求导，分别用θ(u),ω(u)表示：

(1+3u+3u2-3u3)Pi+1+u3Pi+2]

(3+6u-9u2)Pi+1+3u2Pi+2]

角加速度为：

角加速度变化率为：

2 时间最优问题求解

B样条函数的求解以已知各型值点的坐标为前提条件[10]。本文研究的目的为如何在各段连续曲线运动时取得最短时间并满足约束条件，因此，设定粒子群算法的适应度函数为：

(4)

vj≤vmax

(5)

其中，T为机械手臂沿整条轨迹运动的总时间，hi(i=1,2,....m-1)为机械手臂沿每一段B曲线运动所需时间，m为型值点总数，vj(j=1,2,…,6)为各关节的速度，vmax为允许的最大关节速度。

粒子群算法[11]是由J Kennedy和R C Eberhart等于1995年开发的一种演化计算技术，来源于对一个简化社会模型的模拟。该算法中每一个粒子的位置按照下式进行变化：

vi(k+1)=w×vi(k)+c1×r1×(pi-xi(k))+

c2×r2×(pg-xi(k))

(6)

xi(k+1)=xi(k)+vi(k+1)

(7)

其中，vi(k)为第i个粒子第k次迭代时的速度，xi(k)为第i个粒子第k次迭代的位置，pg为群体最好位置，pi为粒子最好位置，c1和c2为权重因子，r1和r2为随机数，w为惯性权重。

粒子群算法步骤如图1所示。

图1 机械手臂粒子群算法过程

3 实验研究

3.1 实验平台及模型建立

本文的研究对象CytonII型机械手臂是具有6个转动关节的6自由度机械手臂。如图2所示

图2 CytonII型机械手臂

图3 机械手臂坐标系示意图

根据D-H法建立的坐标系图如图3所示。

其中，坐标系0、1、3、5的Y轴垂直纸面向里，坐标系2、4、6的Z轴垂直纸面向外。各连杆参数中，θn为连杆n绕关节n的Zn-1轴的转角，dn为连杆间距离，即连杆n沿关节n的Zn-1轴的位移，an为沿Xn方向上连杆n的长度，αn为连杆n两关节轴线之间的扭角。d1=54mm，d3=140.8mm，d5=71.8mm，a2=66mm，a4=71.8mm。各连杆参数见表1所示。

表1 机械手臂连杆参数表

3.2 仿真实验

当机械手臂末端在直角坐标空间中从一点运动到另一点时，由已知的起始点，终止点以及轨迹经过的中间点，通过机械手臂运动学逆解可求出各关节的型值点。本文中各型值点的坐标如表2所示。

表2 节点的数值表

按照上节中采用基于粒子群算法的B样条曲线插值法进行轨迹规划，确定每段曲线的最优时间。将各关节的型值点作为初始种群，则初始种群数为M=10，粒子飞行速度的参数设置为惯性权重w=0.5+r/2，r为0～1之间的随机数。权重因子取为c1=0.05，c2=0.05。r1和r2为[-1,1]之间的随机数。机械手臂关节允许的最大运动速度为vmax=1m/s，轨迹曲线的初始点和终点的速度以及加速度均为0，循环迭代步数取为50步。经过Matlab仿真及计算，取机械手臂前三关节为例，其输出的优化结果见表3所示, 表中hi为每段轨迹运行的时间。

表3 优化结果表

根据实验数据表明，经过粒子群算法优化的B样条轨迹曲线，其各段轨迹运行总时间大约缩短2s左右，达到了实验的预期效果。见图4～图6。

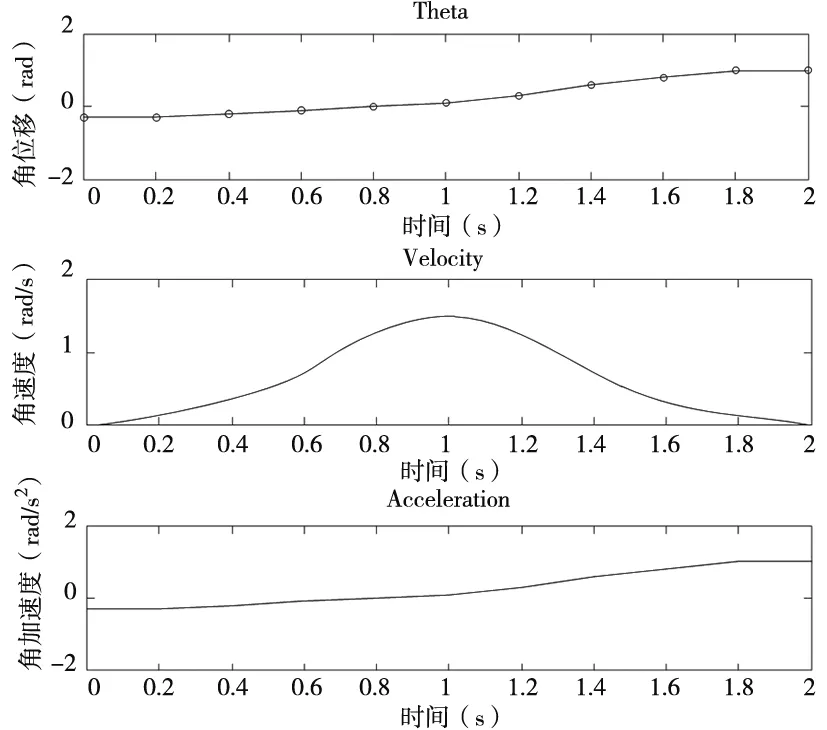
图4 关节1的角位移、角速度以及角加速度

图5 关节2的角位移、角速度以及角加速度

图6 关节3的角位移、角速度以及角加速度

4 结论

本文利用粒子群算法针对机械手臂B样条曲线轨迹规划进行了以最优时间为目标的轨迹规划。经过Matlab仿真及实验分析，通过粒子群算法对各段轨迹的时间间隔进行优化，提高了机械手臂15%～20%的工作效率，更快速、准确地规划出工作轨迹，并能够使机械手臂运行平稳，轨迹平滑连续，有效地避免了机器臂产生震动或碰撞。