机载卫星双星天线运动碰撞检测算法*

吴硕才，徐 雷，张莉萍，李大双

(四川大学 制造科学与工程学院，成都 610000)

0 引言

针对目前一副卫星通信天线只能跟踪一颗卫星的技术瓶颈，以龙伯透镜多焦点特性为理论支撑的双星双通道天线成为未来天线的发展趋势。在双星天线工作过程中，为防止两馈源之间发生“穿透”现象，需要对其进行碰撞检测技术研究。文献[1-4]将机械臂之间的碰撞检测转化为几何基元之间的距离计算，并基于几何分析进行空间线段间的距离计算。但是提出的几何基元多为直线，对于复杂的曲线障碍物没有涉及，并且机器人姿态多样，导致这种方法分类复杂。针对弧线形障碍物，文献[5-8]提出一套基于凸多面体的树形递归结构框架，精确的逼近任意形状的物体。但是这个过程也增大了碰撞检测的计算量。文献[9]采用凸多面体表示检测物体，将最短距离的计算转化为带约束的非线性规划最优解问题，并用遗传算法求解最短距离。该方法计算速度快、精度高，具有一定的有效性。但是该方法也需要提供凸多面体的顶点坐标。

本文结合几何基元和遗传算法各自的优势，针对双星天线两弧形摆臂及馈源之间的碰撞检测，构造一种扫掠体包围体，提出运用遗传算法[10]计算两包围体中心线之间的最短距离的运动碰撞检测计算方法，最后运用MATLAB对所提算法进行数值计算，并在ADAMS建立虚拟样机对数值计算结果进行验证，为双星天线运动路径规划奠定基础。

1 双星天线碰撞检测模型构建

1.1 双星天线简化运动模型

双星天线主要由两对重复的俯仰轴和方位轴、4对电机和减速器、支撑座以及龙伯透镜组成，其中每对电机和减速器驱动一个轴进行旋转，从而使得两个馈源能分别扫描完龙伯透镜的整个半球面，由于两馈源底部处于同一球平面，因此在相互扫描的过程中就有可能发生碰撞。其机构运动简图如图1所示，各关节的运动范围为0°～180°。

1.支撑件 2.方位轴1 3.俯仰轴1 4.方位轴2 5.俯仰轴2 6.馈源 7.龙伯透镜

图1 双星天线机构运动简图

1.2 双星天线碰撞检测几何模型

在进行碰撞检测之前，为了计算的方便，将双星天线可能发生碰撞的部分简化为规则的几何包围盒。目前碰撞检测采取的包围盒有很多，如：AABB、OBB、球形、圆柱形以及K-dops[11]等，但是这些包围盒都存在着只能包围直线型物体，对于双星天线摆臂这种弧线形障碍物则只能通过细分成多个包围盒进行计算，这样大大增加了碰撞检测的计算量。因此，本文提出一种扫掠型包围盒作为摆臂的简化几何基元，以摆臂中心线为指引线，以略大于物体最大边界线的长度为半径画圆，作为扫掠截面进行扫掠，从而形成包围整个摆臂的包围盒。双星天线其他直线型碰撞连杆仍采用圆柱形包围盒作为简化几何基元，其简化之后的几何模型如图2所示。

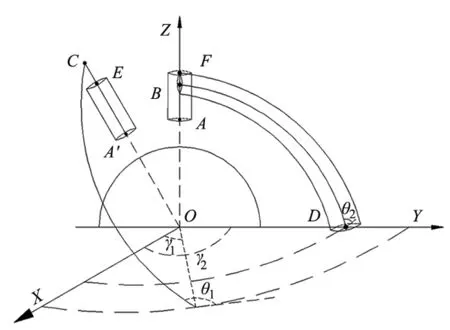
图2 双星天线碰撞检测几何模型

A(A′)点为馈源底部中心点；B点为俯仰轴5拐点；C点——俯仰轴3拐点；D点——俯仰轴5与过球心的水平面交点；E点——A′C上距球心距离与OD和扫掠体半径之和相等的点；γ1、γ2为两方位角；θ1、θ2为两俯仰轴。

由图2可以看出，双星天线碰撞主要包括以下两种情况：俯仰轴3与俯仰轴5两馈源之间、俯仰轴3馈源与俯仰轴5摆臂之间。当碰撞发生在两俯仰轴馈源段之间时，则碰撞段应该为A′E与AF段；当碰撞发生在馈源段与摆臂段时，碰撞段应该为A′E与BD段。在无碰撞检测设备时，可以通过计算碰撞两物体之间的最短距离来判断是否发生碰撞。

2 碰撞检测算法

根据1.2节中的简化几何模型可知，双星天线两俯仰轴之间的碰撞检测能够转化为圆柱体与圆柱体、圆柱体与扫掠体之间的干涉检测。当两个检测基元之间的最短距离小于零，则表示两基元在运动过程当中发生碰撞，反之则不发生碰撞。由于一次检测只能检测两个几何基元之间是否发生碰撞，因此选用圆柱体与扫掠体对碰撞检测算法进行说明。

如图3所示，圆柱体A′E和扫掠体BD分别用集合Ga、Gb表示，中心线分别用La、Lb表示，圆柱半径和扫描圆半径分别用ra、rb表示。圆柱体A′E和扫掠体BD之间的最短距离与两中心线最短距离之间的关系为：

d(Ga,Gb)=d(La,Lb)-ra-rb

(1)

从以上分析可知，求解两基元之间的碰撞检测问题，可以转化为两基元中心线段距离的计算。若d(Ga,Gb)>0，即：

d(La,Lb)>ra+rb

(2)

则两基元不发生碰撞，反之则发生碰撞。

图3 几何基元距离计算

针对传统几何法求解空间曲线距离分类繁杂以及不方便求解曲线与直线之间的距离的问题，本文利用自适应遗传算法的全局最优性求解La与Lb的最短距离。求解空间两曲线之间的最短距离需要遍历两条曲线的整个定义域，如果同时对两条曲线的定义域进行搜索，容易增加求解的复杂度，因此采用文献[12]介绍的交替搜索计算策略进行求解。但是该文献中对于优势个体的选择只采用了精英策略，导致随着种群的不断进化，每一代个体适应度值打的一部分染色体几乎一致，从而使得种群的多样性不断减弱，因此本文采用精英策略与轮盘赌相结合的选择方式，在精英策略的基础上利用轮盘赌增加种群子代的多样性，具体的求解步骤如下：

步骤1：初始种群的生成和编码。在某时刻t时，将直线段La曲线段Lb均分为合适的n段，从每段中随机生成一个点的x坐标，再利用对应的方程求得相应的y、z坐标，从而从La、Lb上分别得到n-1个：P=(P1,P2,…,Pn-1)；Q=(Q1,Q2…Qn-1)。采用二进制编码的方式对各点的x坐标进行编码，形成对应的可以用于遗传算法操作的n-1个二进制串。

步骤2：选择。将La上第i个点pi与Lb上n-1个点之间的最小距离作为该点的适应度函数，即pi的适应度为：

f(pi)=min{d1,d2,…,dn-1}>

(3)

根据La上各点的适应度大小进行选择，对适应度处于前三位的精英个体直接复制到下一代，剩余个体采用轮盘赌算法生成。

步骤3：交叉与变异。对选择后的个体随机选择交叉点和变异点。当种群适应度趋于一致时，应当增大交叉率pc和变异率pm，从而提高种群的多样性避免局部最优或算法早熟；当种群适应度差别较大时，应当采用较低的pc、pm。因此，采用根据种群适应度大小自适应调节交叉率和变异率来进行交叉和变异操作。其公式如下：

(4)

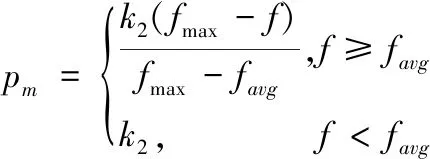
(5)

其中，fhigher为待交叉父代中较大适应度；f为变异个体适应度；fmax为种群中最大适应度；favg为种群平均适应度；

步骤4：判断是否达到最优解。如果迭代次数达到给定的次数或者是其收敛到全局最优解或者近似全局最优解，则算法结束；否则以Lb为研究对象，转向步骤2。即几何基元中心线段距离计算流程如图4所示。

图4 几何基元中心线段计算流程图

重复上述步骤2～步骤4，求解出La与Lc之间的最短距离，再将上述两个最短距离进行比较，从而得出在时刻t时，直线La与直线Lc、曲线Lb之间的最短距离。将求解时刻取为运动的起始时刻到终止时刻，则能够计算出三条曲线之间的实时最短距离。

3 双星天线运动碰撞检测

3.1 双星天线几何基元中心线段数学模型

根据上一节分析可知，想要实现双星天线碰撞检测，只需要比较双星天线障碍连杆几何基元的中心线段距离与两包围盒半径之和的大小即可。由于摆臂的两个终点距离球心的距离相近，为了简化计算，将摆臂简化为圆弧。由此建立双星天线障碍连杆几何基元中心线段的数学模型，其数学模型如图5所示。

图5 双星天线几何基元中心线段数学模型

La、Lb、LC分别表示3个包围盒的中心线段；r1表示A(A′)两点到球心O的距离；r2表示B(D)两点到球心O的距离；rb表示扫描体半径和圆柱体半径。

因此E点距球心点O的距离为：

rE=r2+rb

(6)

F点距球心O的距离为：

rF=r2+rb

(7)

在转过任意θ、γ角度之后，直线段上距球心距离为R的任意点的坐标变化关系为：

(8)

因此，任意转过θ1、γ1、θ2、γ2角度，数学模型中直线段上各点的坐标如表1所示。

表1 数学模型中直线段上各点与两转角变换关系

由几何关系分析可知，D点在转过θ2、γ2角度之后的坐标与θ2无关，只与γ2有关，即坐标关系为(r2·cos(γ2)，r2·sin(γ2)，0)。

已知直线段La过坐标原点、A′以及E三点，因此其空间坐标式参数方程为：

(9)

同理可得直线段Lc的空间坐标式参数方程为：

(10)

对于曲线段Lb而言，由于摆臂呈圆状，因此其可以看成是球面与摆臂平面的交线在x∈[xB,xD]之间的曲线段，故曲线段Lb的空间表达式为：

(11)

其中，向量P=(A0,B0,C0)为过B、D及坐标原点的平面法向量。因此，只需要计算直线段La、Lc、曲线段Lb三者之间的最短距离，从而判断出双星天线是否发生碰撞。由于俯仰轴与方位轴与时间t存在以下关系：

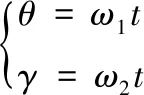
(12)

其中,ω1、ω2表示俯仰轴和方位轴转动的角速度，从而能够对双星天线进行实时碰撞检测。

3.2 数值计算

取初始时刻馈源A′转过的角度为θ01=0°，γ01=90°；馈源A转过的角度θ02=0°，γ02=0°；为了使得两馈源在运动过程中能发生碰撞，取ω1=30°/s，ω2=ω3=15°/s，ω4=6°/s，ω1、ω2、ω3、ω4分别为馈源A和馈源A′的方位和俯仰角速度；r1=50，r2=65，rb=5；取时间t=0～5s。用第2节提到的碰撞检测算法在MATLAB下编程求解，得到最短距离与时间之间的变化曲线如图6所示。

图6 最短距离与时间的变化曲线

从图6中可以看出，当时间t=3.37～3.8s时，双星天线包围盒中心线段之间的最短距离小于包围盒的半径之和，即双星天线在上述路径的运动过程中，当t=3.37s时，开始发生运动碰撞，当t=3.8s时，碰撞停止。

3.3 仿真验证

使用ADAMS对所提算法进行验证。由于双星天线发生碰撞时会产生接触力，因此选用两馈源以及摆臂之间的接触力来验证碰撞的发生。首先在UG中建立双星天线简化模型，将其他不参与碰撞的部分进行省略，并将简化模型导入到ADAMS进行接触力仿真，简化模型如图7所示，初始条件及驱动均与实例计算选取的值保持一致，其结果如图8所示。

1.俯仰轴1 2.馈源1 3.龙伯透镜 4.方位轴2 5.俯仰轴2 6.方位轴1

图7 双星天线简化模型

图8 接触力曲线

从图8中可以发现，双星天线在运动过程中，当t=3.37s时开始产生接触力，而当t=3.8s时，接触力消失。因此，可以确定双星天线在t=3.4s～3.8s之内发生碰撞，与MATLAB中数值求解结果一致，因此验证了算法的正确性。

4 结论

以机载卫星双星天线为研究对象，针对运动过程中的曲线型障碍物，提出一种扫掠体包围盒，从而避免了传统方法使用直线型包围盒分解曲线障碍物的过程，简化了曲线型障碍物包围盒建立过程；同时，针对传统算法不方便求解空间曲线之间距离的困境，提出利用自适应遗传算法的全局最优性计算两包围盒的中心线段的最短距离，并与包围盒的半径之和对比，若最短距离大于半径之和，则不发生碰撞；反之则发生碰撞。最后，用MATLAB对所提算法进行仿真，并用ADAMS对求解结果进行验证，从而验证了算法的正确性，为双星天线运动路径规划奠定基础。