基于人机交互改进A*算法的路径规划研究*

李思良，袁庆霓，胡 涞,黄 鑫，潘珠峰

(1.贵州大学 现代制造技术教育部重点实验室，贵阳 550025；2.台湾清华大学 资讯工程学系,台湾 新竹 30013)

0 引言

随着大规模工业化生产的兴起，数字化装配技术即虚拟装配技术越来越多的应用于实际工业生产。路径规划作为虚拟装配技术的核心，是指以计算机技术、仿真技术和信息技术为支撑，在装配体模型建立和装配序列规划的基础上，利用装配约束信息进行装配路径的求解、判断与分析，并最终生成一条无干涉且最优的装配路径。国内外采用的装配路径规划方法主要可以分为两种：一种是通过装配元件间的配合关系和装配顺序自动计算生成装配路径；另一种是通过人机交互的方式来规划装配路径。目前，虚拟装配路径规划的主流是对路径自动规划与自动搜索的研究，王光慧等[1]对传统遗传算法中变异算子和杂交算子进行了改进，从而提高了算法精确度；张会丽[2]提出了RC*算法，通过随机选取后继节点解决了单项搜索局部最优问题；冯国强等[3]通过A*算法与蚁群算法的结合，实现了局部环境中障碍的规避，并加快了算法全局收敛速度。Mohammad Saiedur Rahaman[4]提出了一种考虑路径可访问性的多目标A*算法，丰富了用户可选择路径范围；KUROSAKA Tsubasa等[5]提出了一种改变局部采样概率进行避障的RRT路径规划算法等。其中针对静态路网问题求解最优路径的A*算法凭借其简单、快速、效率高的特点，被越来越多的研究人员所认同并采用。但是，A*算法大多数还是应用于单层次装配的情况下，对于如何应用于多层次装配并没有进行深入研究及分析。本文通过改进A*算法与人机交互方法的结合，提出了基于人机交互的改进A*算法，算法成功解决了多层次装配体的装配路径规划问题。

1 问题描述

在工业生产中，对复杂装配体进行虚拟装配路径规划是对装配体零部件运用路径规划方法，从而避开环境中的障碍零部件，并最终将装配体零部件无干涉且路径最优地装配起来。构建虚拟装配环境示意图如图1所示。

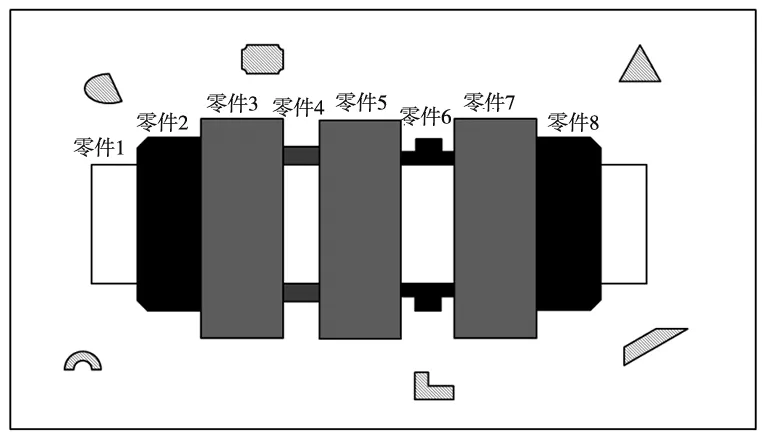
图1 虚拟装配环境示意图

根据图1所示，其中零件1、2、3、4、5、6、7、8组成待装配的装配体，且阴影区域为障碍零部件。针对虚拟装配路径规划问题，根据“可拆即可装”原则，将装配路径规划问题转化为拆卸路径规划问题，即若在图1中无干涉地规划出等待装配的装配体的最优拆卸路径，即得到了装配体的最优装配路径。但在实际工业生产中，当等待装配的装配体零部件结构复杂时，若采用传统装配路径规划方法对装配体进行路径规划会出现组合爆炸的问题。

组合爆炸问题是当一个系统拥有两个以上的有限个子系统时，多个子系统信息相互干扰影响可以构成不同类别的大系统，且构成的大系统数量远远超过子系统数量。针对装配路径规划问题，当装配体结构复杂时，若运用传统路径规划算法对装配体进行路径规划，会导致算法计算复杂性过高，从而出现组合爆炸问题，严重影响装配体路径规划效率。

2 改进A*算法

针对装配体路径规划问题，在传统A*算法的基础上提出改进A*算法。算法对零部件进行了一次大跨步移出场景包围盒的尝试，并引入了干涉威胁概率、平滑度代价、权重系数等参数。改进A*算法实现了不同侧重方向的最优路径寻找，丰富了路径规划多样性，提升了算法效率。

2.1 A*算法

A*(A-mStar)算法是一种在Dijkstra’s方法基础上提出的启发式智能搜索算法，被广泛应用于静态路网中最优路径求解问题。该算法在路径搜索中引入了估值函数，并通过估值函数提前计算节点与目标终点之间的代价值，并以此判断节点是否属于最优路径节点，且优先选择最优估值函数节点为下一路径节点。最终，通过重复这一过程直至节点到达目标终点，以此来确保得到的路径为最优规划路径。A*算法在路径规划问题中启发函数的代价权值为距离，同时距离的估计采用欧氏距离。

在A*算法中，对给定的起始点s(xs，ys)和目标终点e(xe，ye)，且n(xn，yn)为搜寻过程中的某个节点，A*算法的估值函数为：

f(n)=g(n,s)+h(n,e)

(1)

其中，f(n)为起始点s与目标终点e的全局估计代价函数；g(n,s)为起始点s到节点n的实际花费代价函数；h(n,e)为启发项，是当前节点n到目标终点e的预估代价函数。其中:

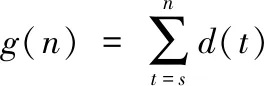
(2)

d(t)为相邻两节点间的距离。

(3)

2.2 改进A*算法

在传统A*算法基础上引入干涉威胁概率、平滑度代价与权重系数参数，令:

g(n,s)=g(n-1)+dne(n,n-1)+P(n)+C(n)

(4)

(5)

其中，dne(n,n-1)为当前节点与上一节点间的距离；P(n)为起始点s到当前节点n的干涉威胁概率；C(n)为路径平滑度代价；式(5)中，Pne(n)为当前节点n到目标终点e的干涉威胁概率；Lne(n)为当前节点n到目标终点e的路径长度代价；ω1,ω2,ω3分别为Pne(n),Lne(n) ,C(n)的权重系数。

改进A*算法通过调节权重系数，可实现不同侧重方向的规划路径选择。当装配体需要选择一条干涉威胁最少的路径时，则设置ω1较大，这样规划出的路径使得装配体面临的干涉威胁最小；当需要保证规划出的路径距离最短时，则设置ω2较大，这样规划出的路径距离最短；当需要规划出平滑度更高的路径时，则加大ω3权重，这样规划出的路径曲线平滑度更高。同时，考虑到对装配体路径规划而言，并不存在确定的目标终点e，即若装配体零部件能无干涉的到达最终拆卸位置，则通过路径反演认为装配路径规划成功。根据刘江山等[6]提出的基于OBB包围盒的A*算法，对装配场景与装配零部件构建碰撞包围盒，并让零部件做一次大跨步移出场景包围盒的尝试，若零部件从当前节点n朝某一确定方向能够无干涉的冲出装配场景包围盒，则认为此路径即为该零部件的最优拆卸路径，且通过路径反演得到该零部件的最优装配路径；若在尝试途中出现干涉的情况，则采取引用权重系数的传统A*算法获取最优装配路径。

3 多层次装配路径规划

针对装配体复杂性提升，若对装配体路径规划运用传统路径规划方法会出现组合爆炸的问题，本文在改进A*算法的基础上通过结合人机交互路径规划方法，提出了基于人机交互的改进A*算法。在基于人机交互的改进A*算法中，人机交互路径规划方法是指在三维装配操作系统中，利用操作者的装配经验，为装配体选择一条无干涉且路线最优的装配路径。针对装配体路径规划问题，将人机交互路径规划方法划分为两个阶段：交互式仿真拆卸阶段与拆卸路径反演得出装配路径阶段。对这两个阶段构建人机交互路径规划方法流程图如图2所示。

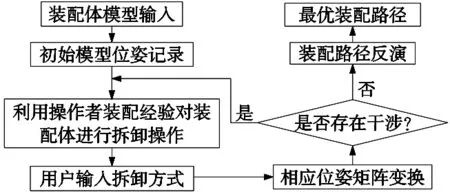
图2 人机交互路径规划方法流程图

根据图2人机交互路径规划算法流程图所示，在交互式仿真拆卸阶段中将装配体模型导入三维装配操作系统，并根据操作者装配经验自定义拆卸方式和拆卸路径，从而保证装配体可以高效无干涉地拆卸成独立的零部件。接下来，在路径反演阶段利用“可拆即可装”原则进行拆卸路径反演，并最终生成装配体装配路径。

本文通过将人机交互路径规划方法与改进A*算法结合，提出基于人机交互的改进A*算法。该算法利用人机交互路径规划方法将复杂装配体分成多个层次段，并对各层次段中的零部件运用改进A*算法进行装配路径规划，最终得到了整个复杂装配体的最优规划路径且成功解决了传统路径规划算法用于复杂装配体路径规划时出现的组合爆炸问题。基于人机交互的改进A*算法流程图如图3所示。

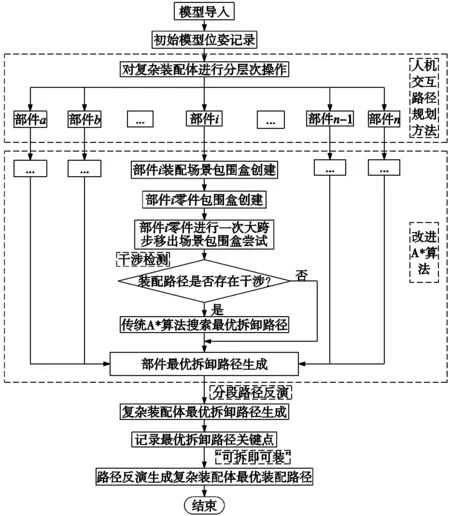
图3 基于人机交互的改进A*算法流程图

根据图3基于人机交互的改进A*算法流程图所示，将算法实现过程划分为以下几个步骤：

步骤1：将装配体三维模型导入虚拟装配操作系统中，并记录模型初始位姿。

步骤2：利用人机交互路径规划方法对装配体模型划分层次，并利用层次树指导装配体拆卸。

步骤3：对已划分层次的装配部件运用改进A*算法来进行装配路径规划。以装配体部件i为例，对装配体部件i各零件及装配场景创建碰撞包围盒，并对零件包围盒进行一次大跨步移出场景包围盒尝试，若尝试过程中无干涉，则该试探路径即为该零件的最优拆卸路径，并根据“可拆即可装”原则，反演生成零件最优装配路径；若尝试过程中有干涉，则利用传统A*算法生成零件最优装配路径。

步骤4：对步骤3中完成路径规划的若干层次段进行分段路径反演，并生成整个装配体装配路径。

值得一提的是，在基于人机交互的改进A*算法中，因为各层次段中零部件装配动作相互无影响，所以其各层次段装配零部件路径规划采用并行输入的方式，此方式不仅节省了装配时间，而且提升了装配效率。

4 实验研究

4.1 仿真结果对比分析

为更明显且直观的表明改进A*算法在复杂装配体路径规划中优于传统路径规划算法，对此进行仿真对比分析。此次仿真基于Intel Core i5-6500；3.20GHz处理器；内存为4GB；操作系统为Windows7的电脑平台实现。在Matlab环境中，对传统A*算法与改进A*算法针对部件零件数(三角面片数)进行算法效率对比如图4所示。

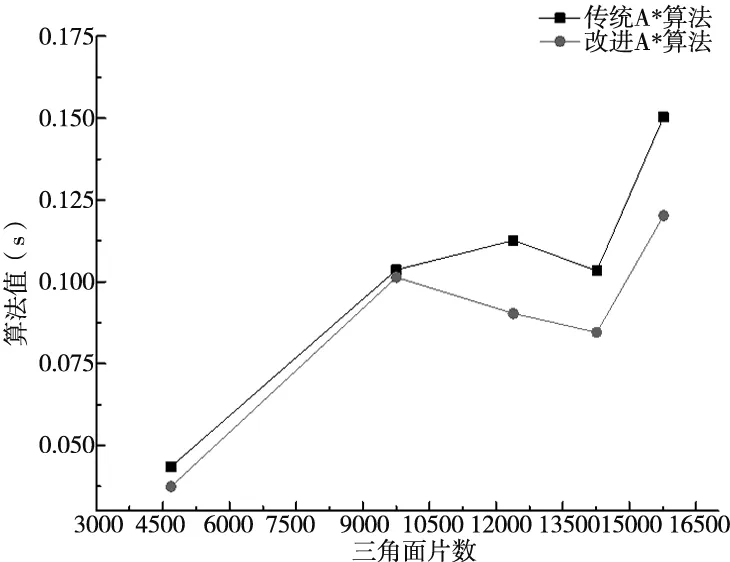
图4 传统A*算法与改进A*算法比较

根据图4算法比较可以看出，当装配部件零件数(三角面片数)较少时，传统A*算法与改进A*算法完成时间相差不大，甚至一度几乎相同，但随着装配部件零件数的增多，因为受组合爆炸问题的困扰，传统A*算法效率落后于改进A*算法，并且当装配部件零件数越多时，改进A*算法的优越性越明显。

在Matlab环境中，针对随机障碍地图，改进A*算法与K-Omega算法(当k=3b=lnfn=0时)从同一起始点出发到同一目标终点的仿真运行结果如图5所示。

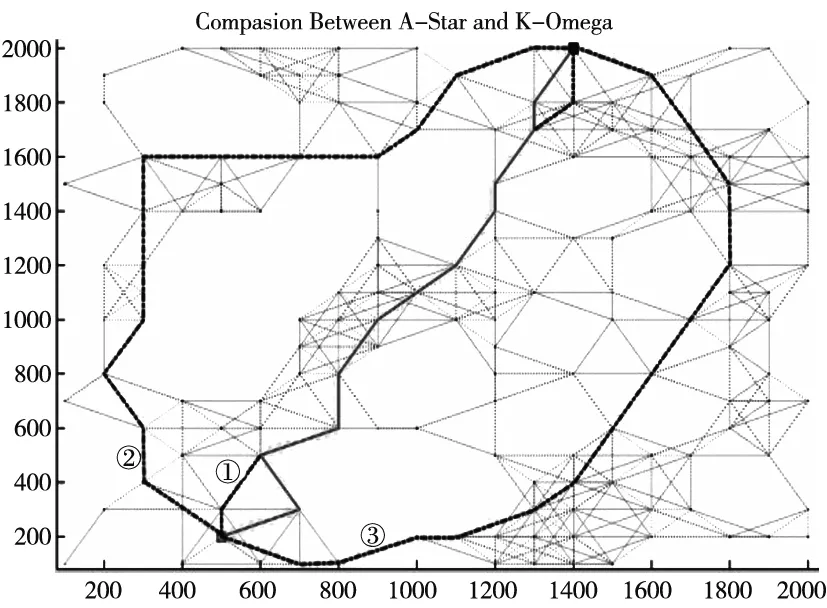
图5 改进A*算法与K-Omega算法比较

在图5中，对改进A*算法取干涉威胁概率、平滑度代价权重为0，路径长度代价权重为1得出了一条距离最短的规划路径①；对改进A*算法取路径长度代价、平滑度代价权重为0，干涉威胁概率权重为1得出了一条干涉威胁最少的规划路径②；对改进A*算法取干涉威胁概率、路径长度代价权重为0，平滑度代价权重为1得出了一条平滑度最好的规划路径③。选取对比方法中最重要的两个参数进行算法运行效率分析如表1所示

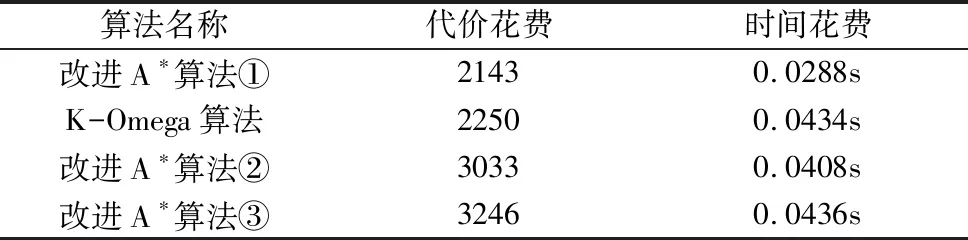
表1 改进A*算法与K-Omega算法运行效率分析

通过表1效率分析得出，当改进A*算法选取路径长度代价权重为1时，其代价花费较K-Omega算法代价花费减少107，时间缩短0.0146s；同时以时间花费为标准，改进A*算法较K-Omega算法效率提升了33.6%，并且从图5中可以直观看出改进A*算法效率远远优于K-Omega算法。

4.2 实例研究

电主轴作为加工中心的核心部件，由打刀缸、内置编码器、主轴等重要部件组成，具有结构紧凑、零部件复杂等相关特点。本文针对电主轴应用传统路径规划方法进行路径规划会出现组合爆炸的问题，采用基于人机交互的改进A*算法进行电主轴路径规划仿真实验。算法利用人机交互路径规划方法对加工中心电主轴进行分层次操作，即将电主轴装配体划分为换刀系统、气缸、主轴、冷却系统等6部分。在装配图中表示电主轴各部分的位置情况如图6所示。

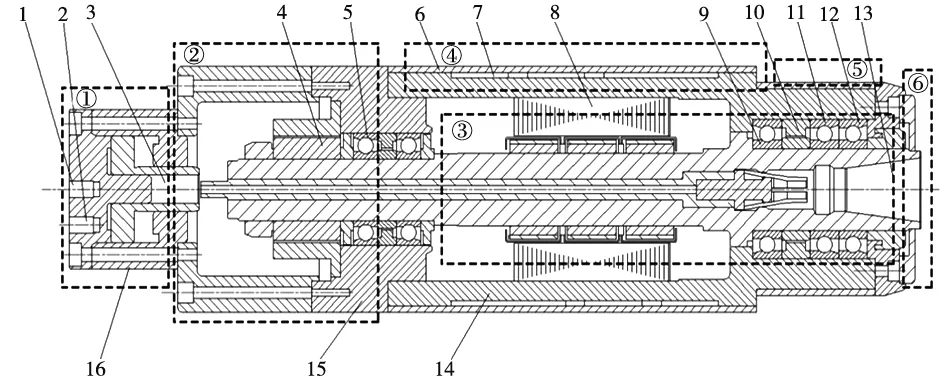
①换刀系统 ②气缸 ③主轴 ④冷却系统 ⑤轴承壳体 ⑥端盖 1.进油口 2.进气口 3.活塞 4.旋转编码器 5.轴承A 6.冷却外壳 7.螺旋水槽 8.电机9.轴承B 10.隔套 11.轴承C 12.轴承D 13.刀柄 14.冷却壳体 15.轴承座 16.打刀缸

图6 电主轴主要部件位置表示

对图6中电主轴主要部件进行层次划分，且层次划分图如图7所示。

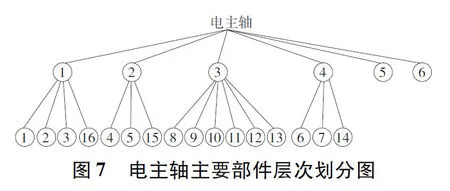
根据图7电主轴主要部件层次划分图，对电主轴进行装配路径规划仿真实验。在Unity虚拟环境下对电主轴利用人机交互路径规划方法进行拆卸分层次仿真实验，实验结果如图8a所示。

(a) 电主轴人机交互路径规划方法仿真

(b) 对主轴进行改进A*算法仿真 图8 仿真图

对图8a中已划分层次的部件进行改进A*算法(取干涉威胁概率、平滑度代价权重为0，路径长度代价权重为1)并行输入获取最优装配路径演示。以主轴部分为例，其中主轴部分的轴承利用改进A*算法进行大跨步移出装配场景包围盒的尝试如图8b中的虚线所示。

通过图4、图5算法之间的比较及图8电主轴在Unity虚拟环境中的路径规划仿真实验，说明基于人机交互的改进A*算法较传统路径规划算法运行效率更高，并可应用于多层次复杂装配体的规划路径寻找，且当装配体零部件结构越复杂时，该算法优越性越明显。

5 结论

本文将人机交互路径规划方法与改进A*算法相结合，提出了基于人机交互的改进A*算法。该算法可高效地规划出复杂装配体的最优装配路径，且有效地避免了装配体组合爆炸的问题。同时，通过对改进A*算法与传统A*算法和K-Omega算法的比较，及对加工中心电主轴的路径规划仿真实验，可以得出本文提出的基于人机交互的改进A*算法节省了复杂装配体路径规划时间，提升了装配效率，使自动路径规划方法应用于实际工业生产成为可能。