宏观经济指标、技术指标与国债期货价格预测——基于随机森林机器学习的实证检验
2019-06-29陈标金
陈标金,王 锋
(华南农业大学 a.经济管理学院;b.集成期货研究所,广东 广州 510642)
一、引言
国债期货价格预测可以为管理利率风险和调控市场利率水平提供依据,因而受到投资者和宏观经济管理部门的重视。国债期货价格预测效果取决于预测变量的选择和预测模型的构建。
在预测变量选择上,众多实证研究表明宏观经济指标对国债期货价格具有预测意义,如Piazzesi和Swanson发现宏观经济和金融市场变量均会影响债券收益率,非农工资增长率可用于预测美国联邦基金期货合约的超额收益率[1];Ludvigson和Ng发现股票指数、利率和物价水平等变量可以用于债券风险溢价预测[2];Duffee发现经济增长率和通货膨胀率会影响债券的收益率,可用于预测债券收益率[3];Altavilla等发现宏观经济意外会对债券收益率产生持续影响,它虽仅能解释债券收益率日变化的1/10,却又能解释债券收益率季度变化的1/3[4];尚玉皇等人发现GDP和通货膨胀对中国中长期国债收益率影响较大[5];丁志国等人发现消费者信心指数变化率、M2 增长率的自然对数、生产者价格指数变化率( PPI) 以及城镇居民失业率等变量可以提高国债收益率的拟合和预测效果[6]。技术指标对金融资产价格具有预测意义也得到大量实证结论的支持,如Park和Irwin的文献综述发现,95篇实证文献中有56 篇的结论支持技术分析法可以获得超额收益,仅20 篇文献认为技术分析法不能获得超额收益[7]。筛选宏观经济指标和技术指标作为预测变量,是国债期货价格预测要解决的首要问题。
在预测模型的构建上,金融资产价格预测模型大致可分为两类:一类是传统统计预测模型,如自回归滑动平均模型(ARMA)、自回归异方差模型(ARCH)及其衍生扩展模型;另一类可归纳为机器学习算法,包括K近邻分类算法、神经网络算法(ANNs)、支持向量机 (SVM)和随机森林(RF)等。Breiman认为随机森林算法不需要考虑多元回归模型中的多重共线性问题,可以加入数千个输入变量,具有明显的优异性[8];Kampichler等比较了5种机器学习算法的预测效果后发现,随机森林的预测效果通常都是最好的[9];方匡南等在对基金裕隆收益率涨跌的预测中发现,随机森林预测准确率远远高于支持向量机、自回归移动平均和随机游走等预测方法[10];方匡南等又在对保险客户利润贡献度预测中发现,随机森林方法要优于传统的类神经网络、CART和SVC等模型[11];涂艳等发现随机森林机器学习预测借款人违约行为的准确率更高[12];王淑燕等使用随机森林算法预测股票涨跌也取得了较好效果[13]。随机森林不需要考虑共线性问题,能够处理高维度数据,对异常值和噪声有很好的容忍度,不容易出现过拟合,预测准确率高,在高维度金融数据预测模型的构建中正在被越来越多的人们所采用[14]。
鉴于此,本文利用2013年9月9日—2017年10月31日5年期国债期货指数序列,运用相关分析、跟踪交易回测和主成分分析筛选宏观经济指标和技术指标,作为国债期货指数预测变量;分别以选取的技术指标、技术指标和宏观经济指标、主成分压缩后的技术指标、主成分压缩后的技术指标和宏观经济指标作为预测变量,利用随机森林算法构建4种国债期货指数预测模型;依据国债期货指数波动集聚性设计跟踪交易规则,通过比较4种RF预测模型的预测精度和跟踪交易收益率,检验宏观经济指标、技术指标和随机森林算法对国债期货指数的预测能力。
二、国债期货指数预测变量的筛选方法
(一)宏观经济指标的筛选
影响国债价格或收益率的宏观经济因素主要包括通货膨胀和经济增长两类。投资者常用消费者物价指数和生产者物价指数度量通货膨胀,常用采购经理人指数度量经济增长动力。同时,考虑到铁路货运量、用电量和银行已放贷款量组成的“克强指数”能够准确衡量中国经济发展状况[15],并已为投资者广泛采用,本文基于数据可得性用M2代替银行已放贷款量,将消费者物价指数(CPI)、生产者物价指数(PPI)、采购经理人指数(PMI)、铁路货运量(RFV)、用电量(EU)、M1、M2等7个指标月同比变化率作为宏观经济指标备选预测变量。
由于被预测变量国债期货指数(P)和预测变量宏观经济指标(X)不一定具有正态分布和等距特性,两者的相关也不一定是线性的。因此,同时计算国债期货指数月收益率与各个备选宏观经济指标月同比变化率之间的Pearson相关系数ρp、Spearman秩相关系数ρs和kendall秩相关系数ρk,并用相关系数的t显著性检验,筛选宏观经济指标作为国债期货指数的预测变量。
(二)技术指标的筛选
技术指标种类繁多,本文选取投资者常用的MACD、KDJ、RSI、WR、PSY、OBV共6种技术指标,从中筛选国债期货指数的技术指标类预测变量。各备选技术指标的计算方法、备选参数和跟踪交易规则设定见表1。
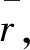
(1)
(2)
(3)
(4)
(5)
其次,针对每一个备选技术指标,筛选各备选参数中跟踪交易年化收益率最高且预测准确率超过50%、年化夏普比率大于1的技术指标,作为国债期货指数的预测变量,即将预测准确率超过50%、跟踪收益率超过市场收益率一个标准差的技术指标,视为对国债期货指数具有预测意义,并纳入预测变量。
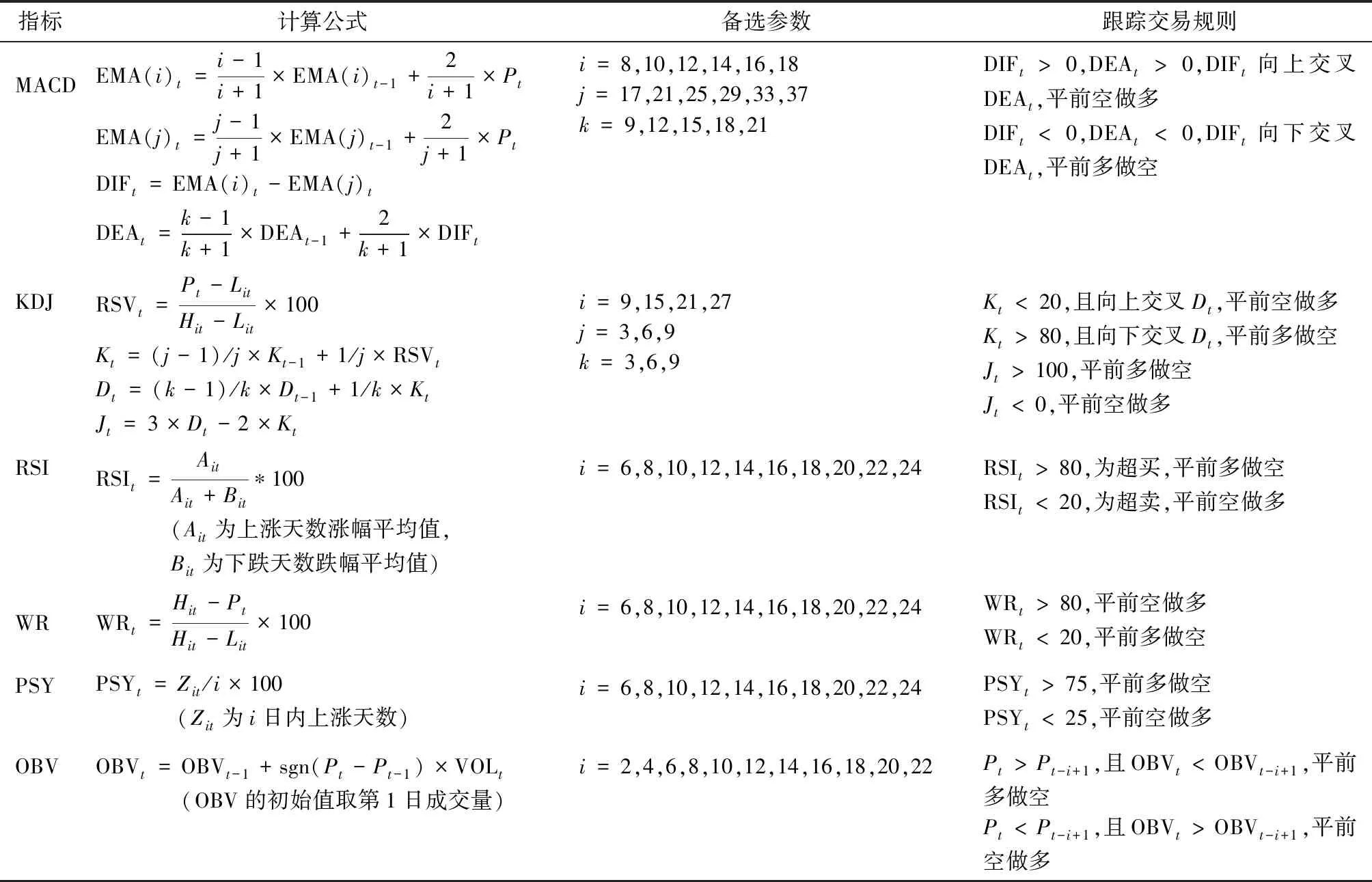
表1 备选技术指标、备选参数及跟踪交易规则表
注:Pt和VOLt分别为第t日国债期货指数收盘价和成交量,Hit和Lit分别为第t日前i日内国债期货指数的最高价和最低价。
(三)预测变量的主成分分析与压缩
用上述方法筛选出的宏观经济指标和技术指标数量较多,如果将其全部纳入国债期货指数的预测变量构建预测模型,各个预测变量包含的信息可能存在重叠交叉,因共线性等问题影响预测模型的精度。主成分分析可以在确保原始信息损失最小的前提下,从多个相关联的变量系统中提取最具价值的少数变量,将多变量系统转化为互不相关但包含了系统主要信息的少数变量系统,在一定程度上能消除变量之间的共线性问题,提高模型的精度。因此,本文对筛选出的宏观经济指标和技术指标预测变量进行主成分分析,以累计贡献率≥90%为标准;再进一步压缩预测变量的个数,并对主成分分析压缩前和压缩后的预测变量,分别构建国债期货指数预测模型,检验预测效果。
三、国债期货指数随机森林预测模型的构建与检验
考虑到金融市场的适应性市场特性,随着市场环境的变化,国债期货指数预测变量和预测模型都可能具有时变特性[16]。因此,对样本序列采用100日滚动训练的方法,以筛选出的宏观经济指标和技术指标为预测变量X,以国债期货指数日收益率R为被预测变量,Rt=(Pt-Pt-1)/Pt-1×100%,利用Breiman提出的随机森林算法动态构建国债期货指数日收益率预测模型,用被预测日前约5个月100个交易日的历史数据滚动建模,逐日向前滚动预测各日收益率;然后,计算国债期货指数日收益率预测值与实际观察值的均方根误差(RMSE)和平均绝对误差(MAE)检验模型的预测精度,设计交易规则回测检验模型的跟踪交易效果。
(一)随机森林预测模型的构建
随机森林(RF)预测模型的构建步骤与方法是:第一步,从实证样本N个交易日时间序列中,导出第1~100个交易日的国债期货指数日收益率及其对应的预测变量序列作为机器学习训练集D,生成随机向量序列{Θi,i=1,2,…,100},采用bootstrap重抽样法从训练集D中随机抽取100个样本生成子样本集,这样重复100次生成100个子样本集Di(i=1,2,…,100);第二步,对每个bootstrap子样本集Di(i=1,2,…,100)分别用随机森林算法建立国债期货指数日收益率树分类模型{h(X,Θi),i=1,2,…,100},假设参数集{Θi}是独立同分布的;第三步,通过100轮训练,得到一个决策树分类序列{h1(X),h2(X),…,h100(X)},再用该序列构建决策树分类模型系统;第四步,将第101日的预测变量X代入这个决策树分类模型系统,以简单多数投票决定第101日国债期货指数日收益率最终分类结果预测值H(X):
(6)
其中I(·)为示性函数。沿着实证样本时间序列向前滚动,重复这4个步骤和方法,用第2个交易日至第101个交易日作为机器学习训练集D构建随机森林预测模型,预测第102个交易日的国债期货指数日收益率;以此类推,逐日向前滚动学习构建预测模型,对下一交易日国债期货指数日收益率作出预测。
分别选取已筛选出的不同指标作为预测变量,遵循上述方法构建4种RF预测模型:模型1的预测变量为已筛选出的所有技术指标;模型2的预测变量为已筛选出的所有技术指标和宏观经济指标;模型3的预测变量为主成分分析压缩后的技术指标;模型4的预测变量为主成分分析压缩后的技术指标和宏观经济指标。通过比较4种模型的预测精度和跟踪交易回测收益率,检验技术指标、宏观经济指标和随机森林模型对国债期货指数的预测能力。
(二)预测精度检验方法
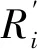
(7)
(8)
RMSE和MAE的数值越小,表示预测精度越高。
(三)跟踪交易回测效果检验方法
利用4种RF模型预测值构建跟踪交易规则,回测跟踪交易收益率,也可以检验预测变量和预测模型的有效性。设计跟踪交易规则的关键在于设定做多和做空的阈值。以国债期货指数日收益率序列标准差的一定比例作为阈值,设计预测模型的跟踪交易规则,即当预测值大于标准差一定比例时做多;当预测值小于负的标准差一定比例时做空。通过比较4种RF模型最优阈值比例系数的跟踪交易收益率,检验预测变量和预测模型的有效性。
考虑到国债期货指数存在波动集聚特性,日收益率序列的标准差是时变的。因此,作为跟踪交易规则阈值的标准差,也应该是被预测日的标准差预测值。与RF滚动建模相对应,用2种方法测算标准差σt的预测值:一是用被预测日前100个交易日的国债期货指数日收益率计算普通标准差,简单外推,作为被预测日标准差预测值σt:
(9)
二是考虑到GARCH(1,1)能较好地识别方差的时变性,用被预测日前100个交易日的国债期货指数日收益率序列构建GARCH(1,1)模型,获得被预测日标准差的预测值σt:
(10)
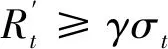
由于年化夏普比率是评估跟踪交易回测效果的综合指标,这里只以SP为依据筛选各RF模型的最优阈值比例系数,比较4种RF模型跟踪交易的最优回测效果;SP>0表示RF模型的跟踪交易收益率好于市场收益率,SP>1表示RF模型的跟踪交易收益率超过市场收益率一个标准差;SP越大,RF模型的预测效果越好。
四、国债期货指数预测与跟踪交易回测实证分析
(一)变量样本数据说明
本文选取5年期国债期货上市当日2013年9月9日—2017年10月31日为实证样本时间区间。第一,被预测变量为5年期国债期货加权指数日收益率,预测变量为宏观经济指标与技术指标,其中备选宏观经济指标为消费者物价指数(CPI)、生产者物价指数(PPI)、采购经理人指数(PMI)、铁路货运量(RFV)、用电量(EU)、M1、M2共7个指标的月同比变化率,备选技术指标为MACD(i,j,k)、KDJ(i,j,k)、RSI(i)、WR(i)、PSY(i)、OBV(i)共6种技术指标;第二,国债期货指数各交易日的开盘价、收盘价、最高价、最低价和交易量数据来源于大智慧行情系统,国债期货指数日收益率和各备选技术指标根据这些市场交易数据计算得到;第三,宏观经济数据来源于东方财富网,由于各备选宏观经济指标是每月公布上个月的月度数据,本文按公布当日更新数的方式构造宏观经济指标日序列,交易日无新宏观经济数据公布则沿用上一日的数据;第四,本文将选取的实证样本分为前后两个时段,用2013年9月9日—2015年12月31日的样本筛选具有预测意义的宏观经济指标和技术指标,然后以选出宏观经济指标和技术指标作为预测变量,用2016年1月1日—2017年10月31日的样本按100日滚动机器学习构建RF预测模型,检验宏观经济指标、技术指标、RF模型的预测和跟踪交易回测效果。
(二)预测变量筛选结果
1.宏观经济指标筛选结果。2013年9月—2015年12月,国债期货指数月收益率与7个备选宏观经济指标前一个月同比变化率的Pearson相关系数ρp、Spearman秩相关系数ρs、kendall秩相关系数ρk的计算结果如表2。在5%的显著性水平下,国债期货指数月收益率除了与M1的月同比变化率不相关外,与CPI、PPI、PMI、铁路运量(RFV)、用电量(EU)、M2的月同比变化率都显著负相关。因此,本文选取CPI、PPI、PMI、RFV、EU、M2的月同比变化率6个宏观经济指标作为国债期货指数的预测变量。
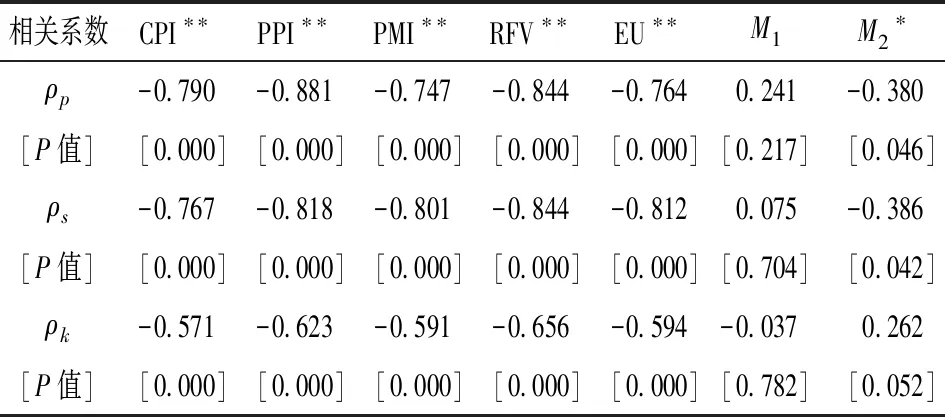
表2 国债期货指数月收益率与宏观经济指标月同比变化率相关系数表
注:*、**分别为5%、1%显著性水平下相关显著。
2.技术指标筛选结果。遵循表1和式(1)~(5)的方法,用2013年9月9日—2015年12月31日国债期货指数日交易数据,分别针对MACD(i,j,k)、KDJ(i,j,k)、RSI(i)、WR(i)、PSY(i)、OBV(i)6种技术指标的各备选参数进行跟踪交易回测。以年化收益率最高且预测准确率超过50%、年化夏普比率大于1的标准,对每一技术指标技术各备选参数进行筛选,结果如表3。表3中,MACD(8,17,9)、KDJ(9,6,3)、WR(6)、PSY(6) 的预测准确率都在60%以上,跟踪交易年化夏普比率均大于1.8,对国债期货指数具有很强的预测能力,本文将这4种技术指标选为国债期货指数的预测变量。
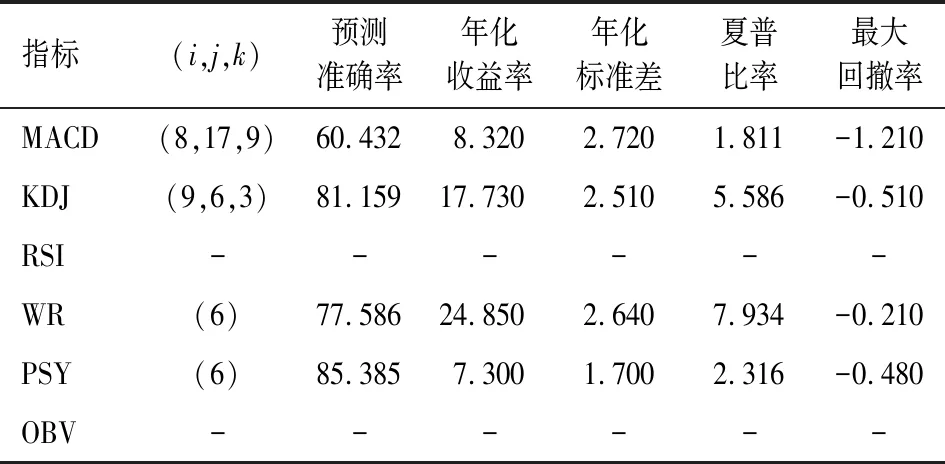
表3 技术指标最优参数筛选结果表
注:-为没有符合筛选标准的参数。
(三)4种RF模型的预测精度比较
用2016年1月1日—2017年10月31日的样本数据,按照式(6)以100日滚动机器学习构建RF模型。针对不同的预测变量构建4种RF模型:模型1的预测变量是筛选出的4种技术指标;模型2的预测变量是筛选出的4种技术指标和6个宏观经济指标;模型3的预测变量是取累计贡献率90%以上主成分压缩后的技术指标;模型4的预测变量是取累计贡献率90%以上主成分压缩后的技术指标和宏观经济指标。根据式(7)~(8),4种RF模型国债期货指数日收益率预测值与实际观察值的均方根误差(RMSE)和平均绝对误差(MAE)的计算结果如表4。

表4 4种RF模型预测误差比较表 单位:%
比较4种RF模型的预测精度可以看出:首先,模型2的RMSE和MAE都小于模型1,模型4的RMSE和MAE都小于模型3,即同时用技术指标和宏观经济指标作为预测变量构建的RF模型,预测精度总要优于只用技术指标作为预测变量构建的RF模型,这表明宏观经济指标对国债期货价格具有预测意义,基本分析法有助于提升国债期货价格预测的准确性;其次,模型3的RMSE小于模型1,但MAE大于模型1;模型4的RMSE小于模型2,但MAE大于模型2,这表明用主成分分析压缩预测变量个数并不一定能改善RF模型的预测精度。
(四)4种RF模型的跟踪交易回测效果比较
分别用式(9)式(10)的预测标准差作为阈值设计基础,选取阈值比例系数γ=0.05、0.10、0.25、0.5、0.75、1.0的6个比例,按前文设计的跟踪交易规则对4种RF模型2016年1月1日—2017年10月31日间预测值的跟踪交易回测效果如表5。
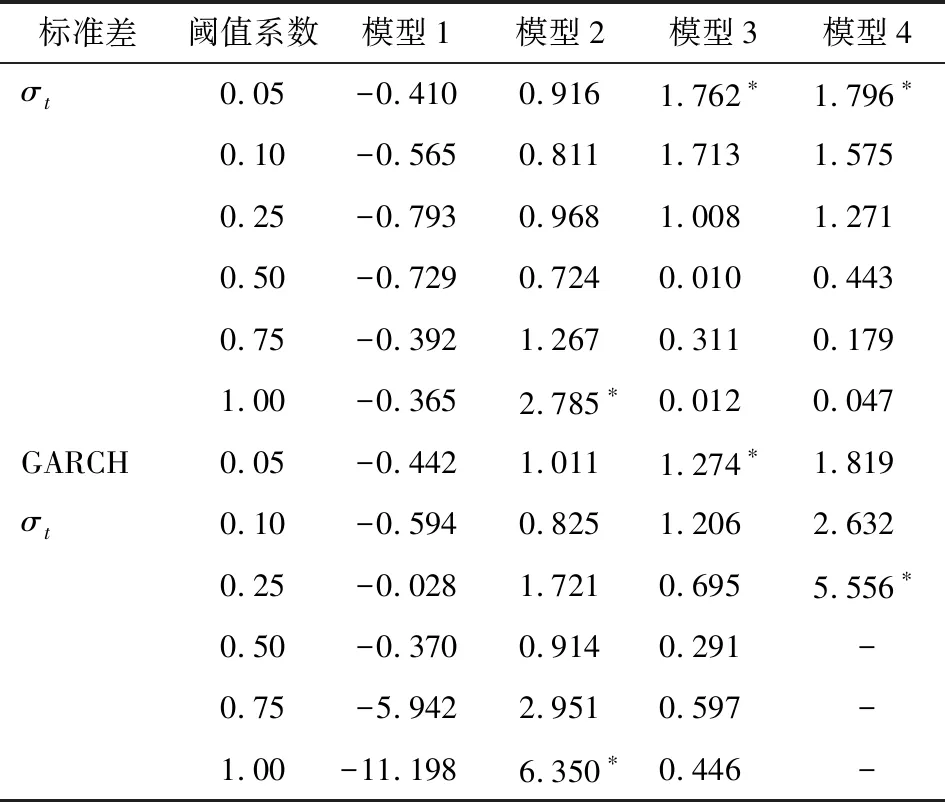
表5 4种RF模型跟踪交易回测效果年化夏普比率表
注:*为跟踪交易的最优回测年化夏普比率,-为回测中没有交易机会。
比较4种RF模型的跟踪交易回测效果可以看出:
首先,以主成分分析压缩后的技术指标为预测变量构建的RF模型具有预测能力,但以多种技术指标构建的RF模型,跟踪交易收益率不如单个技术指标的经验交易规则;模型3的最优回测年化夏普比率大于1,模型1的回测年化夏普比率却小于0,而且模型3和模型1的回测年化夏普比率都远远小于表3中单个技术指标经验交易规则,这显示出只经过100个交易日短期学习训练的RF模型,不能同时有效识别多个技术指标的预测规则;主成分分析压缩技术指标个数可以提高RF模型的预测效果,但利用技术指标构建RF模型预测效果总体不如有经验的交易者采用单个技术指标的预测效果。
其次,在技术指标基础上再将宏观经济指标引入预测变量构建RF预测模型,可以明显提高模型跟踪交易收益率;各阈值的回测年化夏普比率模型2普遍大于模型1,模型4普遍大于模型3,无论以普通标准差还是GARCH标准差作为阈值基础,最优回测年化夏普比率也是模型2大于模型1,模型4大于模型3,这进一步验证了宏观经济指标对国债期货指数具有预测意义。
再次,用主成分分析精选宏观经济指标和技术指标构建RF模型,兼顾国债期货价格的波动集聚特性构建跟踪交易规则,可以取得很好的预测精度和跟踪交易收益率。模型4和模型2的最优回测年化夏普比率分别高达5.556和6.350,表明精选宏观经济指标和技术指标构建RF模型预测国债期货指数是有效的。
五、结论与启示
首先,本文通过相关分析和跟踪交易回测,筛选出CPI、PPI、PMI、铁路运量(RFV)、用电量(EU)、M2的月同比变化率6个宏观经济指标和MACD(8,17,9)、KDJ(9,6,3)、WR(6)、PSY(6)4种技术指标,作为国债期货指数的预测变量;其次,考虑国债期货指数预测变量和预测模型都可能存在时变性,分别以技术指标、技术指标和宏观经济指标、累计贡献率90%以上主成分压缩后的技术指标、累计贡献率90%以上主成分压缩后的技术指标和宏观经济指标为预测变量,利用随机森林算法按100日滚动训练,动态构建了4种国债期货指数日收益率RF预测模型;最后,依据国债期货指数波动集聚性设计跟踪交易规则,通过比较4种RF预测模型的预测精度和跟踪交易收益率,检验了宏观经济指标、技术指标和随机森林算法对国债期货指数的预测能力,结果发现:第一,精选越少的技术指标作为预测变量对国债期货指数的预测效果反而越好,以多种技术指标构建的RF模型,跟踪交易收益率不如单个技术指标的经验交易规则;第二,在技术指标基础上再引入宏观经济指标构建RF模型,能明显提高RF模型对国债期货指数的预测精度和跟踪交易收益率;第三,精选宏观经济指标和技术指标,利用随机森林算法构建动态国债期货指数RF预测模型,依据价格波动集聚性设计跟踪交易规则,能够取得很高的跟踪交易收益率。
从这些实证结论中至少可以得到三点启示:一是宏观经济指标对国债期货价格具有预测意义,基本分析法有助于提高国债期货价格的预测效果;二是技术分析法对国债期货价格也具有预测意义,国债期货投资中遵循精选的单个技术指标跟踪交易收益率更高;三是可以利用随机森林算法,依据价格波动集聚性设计跟踪交易规则,构建有效的国债期货人工智能量化投资模型。
