基于SVM的套管最大von Mises应力预测方法
2019-06-28狄勤丰吴志浩王文昌覃光煦
狄勤丰, 吴志浩, 王文昌, 覃光煦, 陈 锋
(上海大学应用数学和力学研究所,上海 200072)
随着超深井、定向井、水平井的逐渐增多,复杂载荷作用下套管的应力计算问题越来越受到关注。目前的研究主要针对居中套管(包括偏磨)在均匀和非均匀地应力条件下的强度计算[1-9],但在非均匀地应力条件下无法求得不居中套管应力的解析解,W.J.Rodriguez[10],P.D.Pattillo[11]和A.Nabipour[12]等人利用有限元方法进行了研究,只有窦益华[13]讨论了解析求解方法,提出了解决此类问题的新思路。在实际工程中,由于所遇情况复杂多变,常常需要针对不同对象进行有限元建模和分析,所需周期长,很难满足快速、实时解决问题的要求。为此,笔者提出了一种基于支持向量机(support vector machine,SVM)的非均匀地应力条件下不居中套管最大von Mises应力的快速预测方法,并对φ311.1 mm垂直井眼中的套管进行了分析研究。
1 SVM原理及其Matlab实现
SVM是一种基于统计学习理论的机器学习算法,通过寻求结构风险最小化来实现实际风险的最小化,在有限信息条件下得到最优结果[14],在解决小样本、非线性和高维模式识别问题中表现出许多特有的优势。SVM可以作为一种广义的线性分类器,它的原理是利用非线性变换将输入空间变换到一个高维的特征空间,并在新的空间寻找最优线性分界面。线性可分的情况下,为确保经验风险最小,选取最优分界线H时不仅需要分类准确,还要使分类间隔M(H1和H2之间的距离)最大[14],如图1所示。
线性不可分情况下,SVM的主要思想是将输入向量x映射到一个高维的特征向量空间,用特征向量φ(x)来代替,从而得到最优分类函数。由于在运算过程中,无论是目标函数还是决策函数都只涉及到训练样本之间的内积运算,而原空间的核函数可以取代该内积运算,因此可通过选择合适的核函数完成从线性问题到非线性问题的推广[14]。
支持向量机回归算法(support vector regression,SVR)是SVM的衍生算法,其本质是需要寻求一个最优超平面,使所有样本点与该超平面的总体偏差最小[15]。也就是说,对于一个容量为n的样本集:
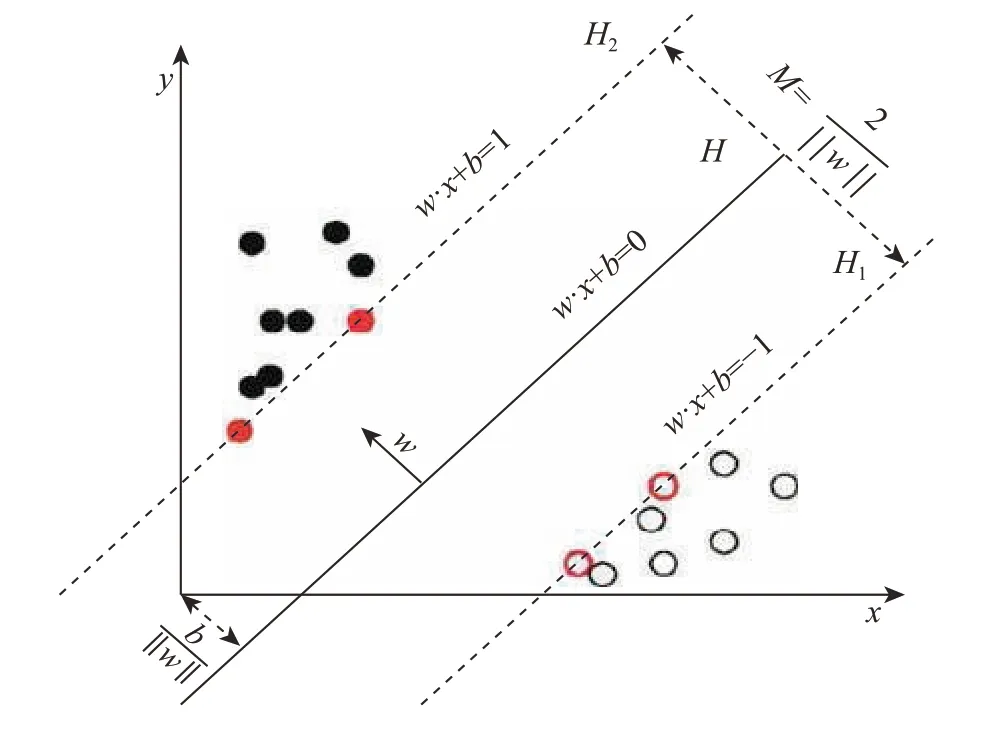
图1 线性可分情况下的最优分类线[14]Fig.1 Optimal classification line in the case of linear separability[14]

式中:i 为样本序号;d为xi的维数。
需要寻找一个最优回归函数f,使f(xi)尽可能接近对应的样本值yi。
通过构造Lagrange函数,将支持向量机回归问题转化为凸二次规划寻优的对偶问题[15]:

其中
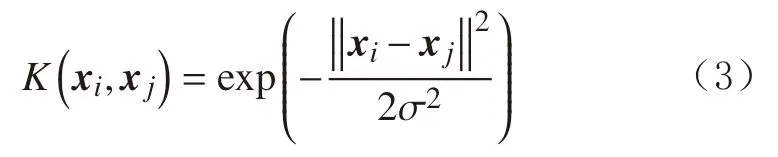

式中:bo为回归参数值。
式(4)即为基于径向基核函数的ε-SVR 模型。
ε-SVR模型的回归效果主要受核函数参数σ、不敏感系数ε及惩罚因子C等参数的影响[16-17]。通过比较各种参数优选的方法,选用网络搜索法进行参数寻优[18],以训练样本均方根误差(root mean squared error,RMSE)最小作为寻优标准,即:
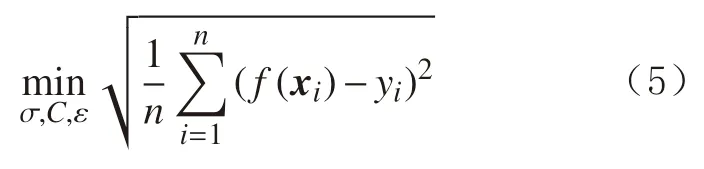
式中:f(xi)为预测值。
基于Matlab软件,可以实现程序运算,具体运算框图见图2。
2 SVM实验样本构建
为了利用SVM方法实现非均匀地应力和套管不居中情况下套管最大应力的预测,必须建立实验样本。由于实际的“套管-水泥环-地层”系统及其受载十分复杂,这些样本无法用真正的实验方法构建,为此利用ANSYS有限元方法进行“实验样本”的构建。关于“套管-水泥环-地层”系统的有限元分析已十分成熟,也已经过实际数据的验证。这种有限元分析的一个特点是在弹性条件下计算套管的应力,最后根据应力大小和套管的强度来确定套管是否失效[19]。本文的“实验样本”也基于弹性条件进行构建。
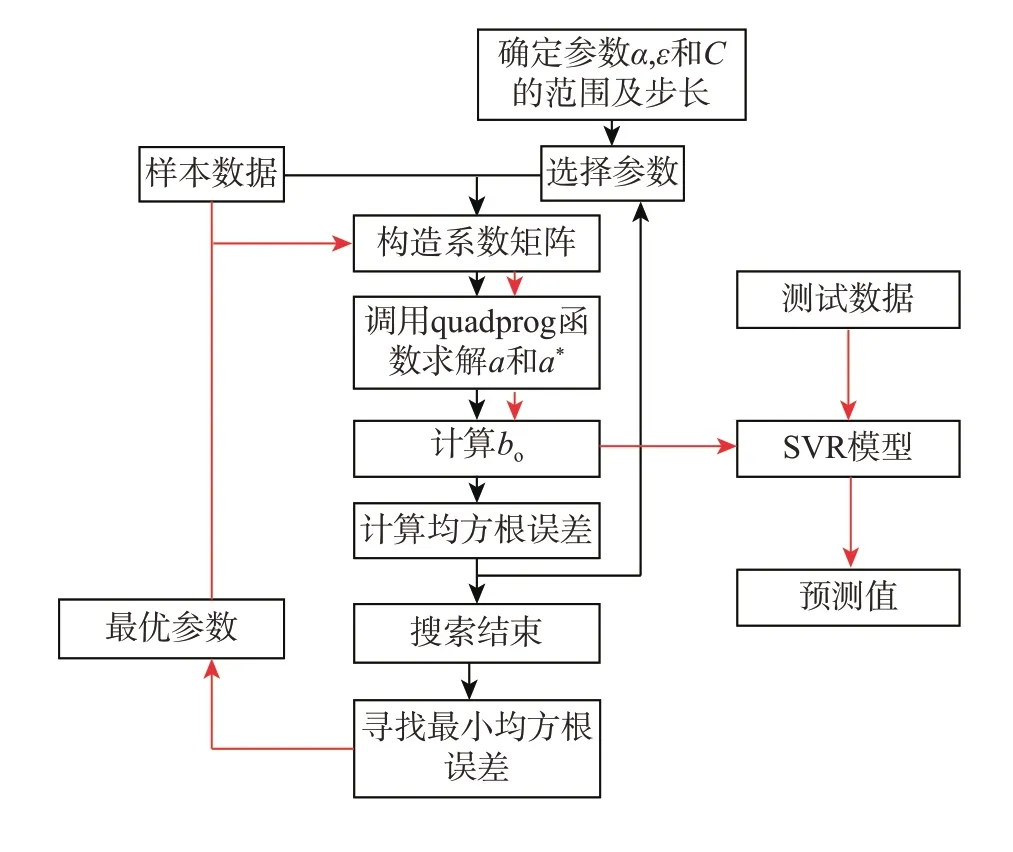
图2 ε-SVR模型的MATLAB程序实现Fig.2 MATLAB program implementation of the ε-SVR Model
影响“套管-水泥环-地层”系统套管应力的因素很多,包括套管的类型和尺寸、最大及最小水平地应力、钻井液密度、水泥环的弹性模量及泊松比、地层的弹性模量及泊松比、套管偏心距和偏心角。关于地应力的影响,有不同的观点,但对于刚钻穿盐膏层的井筒来说,由于应力释放需要较长的时间,因此在一定时间段内,套管将会承受非均匀地应力的作用。同时,研究表明,最大应力一般出现在偏心角为90°或270°的方向[20]。为了减少模型变量,提高预测效率,在构建“实验样本”时,将偏心角固定为90°。同时,当套管给定时,其类型和尺寸都将确定。因此,针对给定套管进行应力预测时,将主要包含最大地应力、最小地应力和水泥环特性等8个关键影响因素。由于实际情况非常复杂,很难确定上述影响因素的合理范围,因此采用了文献调研和实际调查的方法,确定了影响因素的近似取值范围,见表1[21-22]。

表1 主要影响因素及取值范围Table 1 Main influencing factors and range of values
某典型的“套管-水泥环-地层”系统如图3所示,井眼直径为311.1 mm,套管内径为219.0 mm,套管外径为250.8 mm。假设套管在井眼中的偏心距为δ,偏心方位角为φ,最大水平主应力σH沿x方向,最小水平主应力σh沿y方向。对几何模型进行单元划分,单元类型选择二维四边形PLANE183单元,按内密外疏的方式划分网格。划分后的网格如图4所示,共计6 215单元,18 953节点。对其施加载荷及约束,偏心方位角固定为90°,分别计算不同偏心距时的套管von Mises应力分布及其最大值。
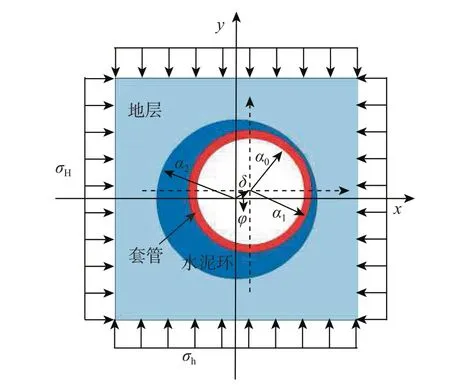
图3 套管-水泥环-地层系统几何模型Fig.3 Geometry model for casing, cement sheath and formation

图4 套管-水泥环-地层系统有限元模型Fig.4 Finite element model for casing, cement sheath and formation
某一工况下对应的计算参数:偏心距为1.5 mm,σH为92.0 MPa,σh为59.0 MPa,地层弹性模量和泊松比分别为30 GPa和0.27,水泥环的弹性模量和泊松比分别为35 GPa和0.17,套管的弹性模量和泊松比分别为210 GPa和0.30,钻井液密度为1.64 kg/L,对应井深为4 995.00 m,钻井液静液柱产生的内压约8.03 MPa。地层用以井筒为中心、边长为3.00 m的正方形代替,该工况下的套管内壁von Mises应力云图见图5。从图5可以看出,套管内壁沿y方向(即最小水平主应力方向)的von Mises应力最大达321 MPa。

图5 套管内壁von Mises应力云图Fig.5 von Mises stress cloud diagram on the casing inner wall
类似地,可计算得到其他99个“实验样本”数据的最大von Mises应力,因样本数量较大,只给出了1~10号和91~100号样本计算结果(见表2),并将1~95号样本作为训练样本,96~100号样本作为测试样本。为了避免人为干扰,计算过程中,每一个因素的取值都采用随机方法。
3 套管最大von Mises应力预测及精度分析
基于SVM的非均匀地应力条件下不居中套管最大应力预测,关键在于确定ε-SVR模型的3个核心参数,即σ、ε和C的寻优,这需要在一定范围内对3个参数进行搜索。笔者选择σ的范围为[0.1,3.0],搜索步长为0.01;ε的范围为[0.01,3.05],搜索步长为0.05;C的范围为[1,10],搜索步长为0.1。经参数寻优,最佳的σ、ε和C值分别为2.01、0.01和3.00。基于这3个模型参数,预测得到表2中96~100号参数对应的最大应力值(见表3和图6)。为了比较,同时列出了对应的样本值。
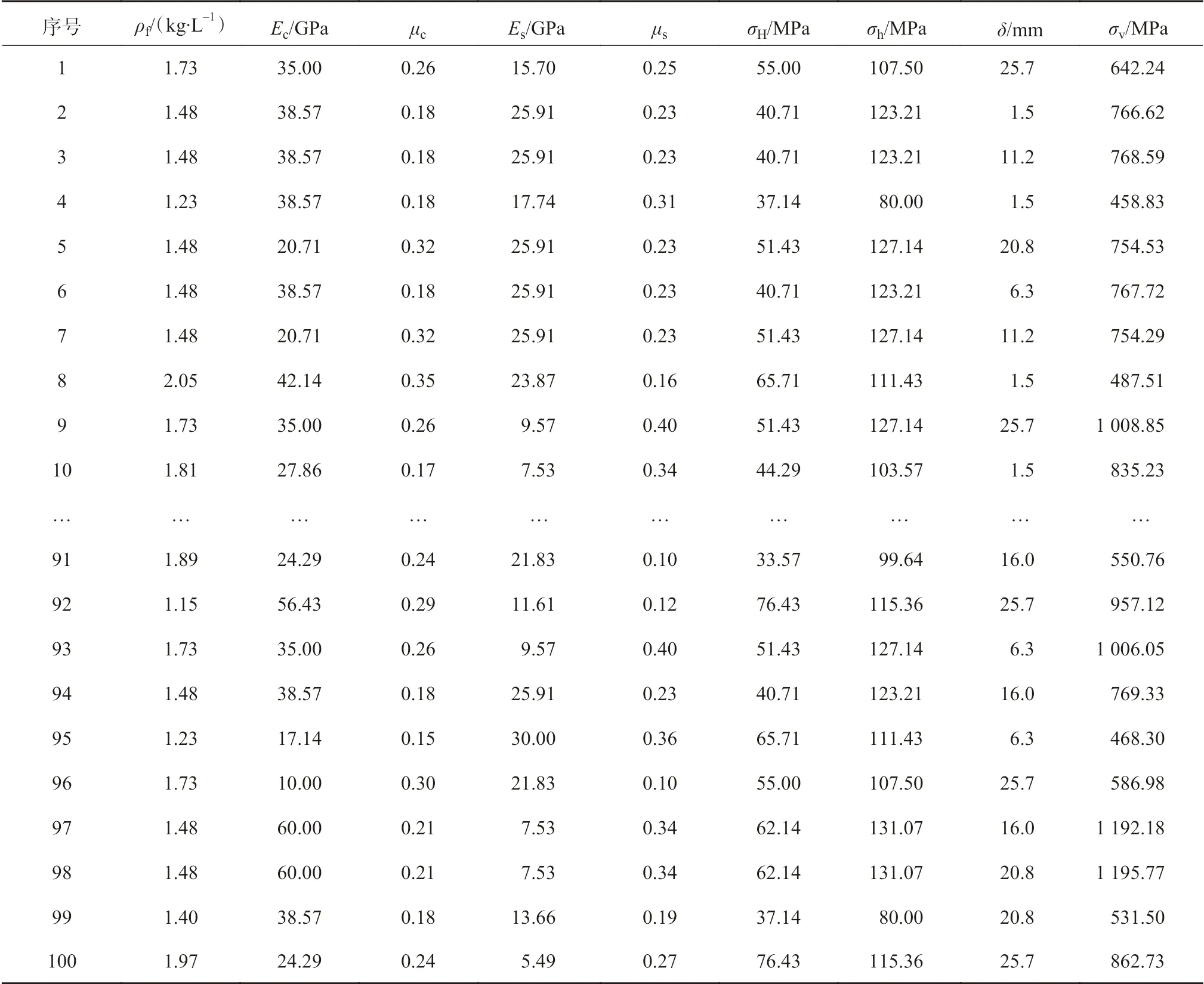
表2 SVM“实验样本”数据Table 2 Data of the SVM “experimental samples”

表3 测试样本的预测结果Table 3 Predictive effect of test samples

图6 预测值和样本值对比结果Fig.6 Comparison of predicted and sample values
从图6可以看出,95个训练样本的预测结果和样本值基本重合,表明训练样本的拟合精度很高。5个测试样本的相对误差分别为2.76%、0.70%、1.00%、-0.12%和-2.01%,平均相对误差仅为1.32%。可见,利用SVM方法,可以快速预测非均匀地应力条件下不居中套管的最大von Mises应力。
4 结论与建议
1)非均匀地应力条件下,目前主要采用有限元分析方法求解不居中套管的应力,缺少数值解,给套管强度校核带来了不便。利用基于SVM的智能预测方法可以解决这一难题,为实际套管应力预测提供了一种新的方法。
2)基于径向基函数的ε-SVR 模型的预测精度较高,测试样本预测值与“实验样本”“真实值”的平均相对误差仅为1.32%。
3)在已知影响因素合理范围内,利用有限元分析方法可以获得大量的“实验样本”,不但成本低,而且速度快,为利用SVM方法解决套管应力预测难题提供了有效手段。
4)本文仅以一种套管为例进行了最大von Mises应力SVM预测,对于其他种类套管,需要重新进行“实验样本”计算和ε-SVR模型关键参数寻优。在保证计算获得的“实验样本”准确可靠的前提下,可以采用该方法预测各种套管的最大von Mises应力。
