大位移井钻井延伸极限研究与工程设计方法

高德利， 黄文君， 李 鑫

（石油工程教育部重点实验室（中国石油大学（北京）），北京 102249）

大位移井最早出现于20世纪20年代，美国首次在加利福尼亚州从陆地钻大位移井以开发海上油气田[1]。随后，挪威北海西Sleipneer、Statfjord和Oseberg，美国Pedernales和Dos Guadras，英国Wytch Farm和Gullbaks等油田都进行了大位移井油气开发工程实践，初步形成了一套较为成熟的大位移井工程技术，并获得了良好的经济效益和社会效益[2-3]。进入21世纪后，随着钻井技术突飞猛进的发展和油气勘探开发需求的不断增加，大位移井钻井技术得到了长足发展，大位移井井深或水平位移的世界纪录也被不断刷新[3-10]。目前，创世界纪录的大位移井主要集中于英国的Wytch Farm油田、俄罗斯的萨哈林地区和美国的墨西哥湾地区等。我国大位移井钻井完井技术研究也取得很大进展[11-19]，并相继在南海东部西江24-1油田和流花11-1油田钻成了XJ24-3-A14大位移井（水平位移8 063 m，创造了当时水平位移最大世界纪录）[3]和B3ERW4大位移井（水垂比4.58，创造当时水垂比最大国内纪录）[20-21]。

全球大位移井钻井实践表明，虽然大位移井井深、水平位移或水垂比的世界纪录被不断刷新，但是每一项大位移井世界纪录都受当时的主客观约束条件影响，大位移井钻井延伸极限仍难以预测和控制。在特定的主观和客观约束条件下，任何一口大位移井的钻井作业井深（亦称“测深”）都存着一个极限值，称之为大位移井钻井延伸极限。图1所示为世界主要定向井的垂深和水平位移统计结果[22]，其中数据点的外包络线（即图中红色曲线）为当前约束条件下能够达到的大位移井钻井延伸极限，其中横向极限（即水平位移）随着垂深增大呈现出“迅速增大—稳定—线性降低”的基本变化趋势。实际上，随着钻井技术与装备水平的不断提高，外包络线也在不断拓展。

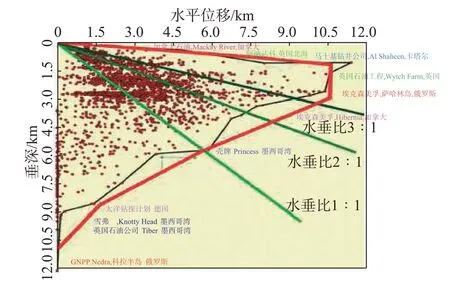
图1 世界定向钻井统计结果[22]Fig.1 Statistics data of directional drilling in the world[22]

随着油气资源勘探开发约束条件的变化，对大位移井、特别是大位移水平井及丛式井的需求越来越大，所面临的技术挑战也越来越大。为了合理评估和降低大位移井的工程作业风险，国内外开展了大位移井钻井延伸极限研究，以期在工程技术和经济效益合理的基础上，尽可能提高大位移井钻井延伸极限。为此，笔者在总结大位移井工程技术发展现状的基础上，重点介绍了大位移井钻井延伸极限的理论研究进展，以期为推动我国大位移井钻井技术发展提供指导和借鉴。

1 大位移井钻井延伸极限研究概述

国外对大位移井钻井延伸极限的相关研究与应用比较早。1994年，R.Meertens等人[23]从井身结构设计及钻井风险的角度，对英国TA-05大位移井的延伸极限进行了分析。1995年，J.Wu等人[24]研究了油管在下入过程中的屈曲行为，进而推导出油管在水平段的下入极限，认为螺旋屈曲是限制油管下入极限的首要因素。2003年，L.A.S.Rocha等人[25-26]指出，随着井深的增加，所钻地层破裂压力的增加幅度不能与环空压耗保持同步，因此大位移井钻井存在一个延伸极限值。其他国外学者基于大位移井工程实例，分析了地层、钻井装备和水力条件等相关因素对延伸极限的影响[27-32]。

国内学者也开展了大量的大位移井钻井延伸极限理论研究。高德利等人[1,9]首次系统提出了大位移井钻井延伸极限的基本理论概念，指出在大位移井钻井工程中需要考虑裸眼延伸极限、机械延伸极限和水力延伸极限等3种极限状态，引领了国内大位移井钻井延伸极限的理论研究。汪志明等人[33]建立了大位移井钻井水力延伸极限的计算模型，分析了地层、钻井泵、环空压耗及岩屑床高度等因素对水力延伸极限的影响；闫铁等人[34]应用大位移水平井整体钻柱摩阻分析的间隙元理论，给出了大位移水平井机械延伸极限的计算模型；Chen Xuyue和Gao Deli[35]给出了海洋超大位移井钻井裸眼延伸极限的计算模型；其他学者也从不同的角度研究了不同因素对大位移井钻井延伸极限的影响[36-41]。

2 大位移井钻井延伸极限理论研究

大位移井钻井延伸极限研究前期主要针对工程实践进行分析总结，近年来开展了较多理论研究并取得了一些创新成果[1]。通过开展大位移井钻井延伸极限理论研究，可以定量预测大位移井钻井延伸能力，以期规避工程作业风险，防止钻井恶性事故的发生；同时，可以对大位移井工程设计进行了优化，以提高定向钻井的水平位移延伸作业能力。

2.1 大位移井钻井延伸极限的概念

在特定的主观和客观约束条件下，任何一口大位移井的钻井作业井深都存着一个极限值，称之为大位移井钻井延伸极限，包括裸眼延伸极限、机械延伸极限和水力延伸极限等3种极限。其中，裸眼延伸极限是指裸眼井底被压破或渗漏时的大位移井井深，主要取决于实钻地层的安全钻井密度窗口及钻井环空多相流循环压耗；机械延伸极限包括大位移井钻柱作业极限和下套管作业极限，主要取决于大位移井的导向控制模式（滑动导向或旋转导向）、管材强度、井眼约束、管柱载荷和钻机功率等；水力延伸极限是指在能够保持钻井流体正常循环及井眼清洁的前提下，钻井水力允许的井深，主要取决于钻井机泵、钻柱、地面管汇、水力参数和机械钻速等。在大位移井钻井优化设计与风险控制时，应该根据具体的主观和客观约束条件定量评估大位移井钻井的裸眼、机械及水力等延伸极限值，取其最小值作为大位移井钻井延伸极限。

2.2 大位移井钻井延伸极限预测模型

2.2.1 大位移井钻井裸眼延伸极限

2009年，笔者考虑实钻地层和钻井环空多相流的综合影响，建立了大位移井钻井裸眼延伸极限预测模型[9]：

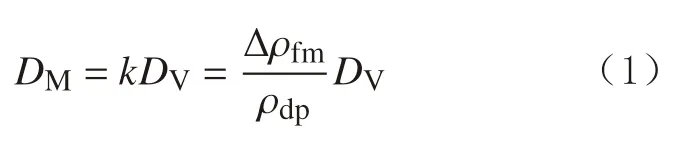
式中：DM为大位移井钻井裸眼延伸极限，m；k为测垂比（即测深与垂深之比）；Dv为大位移井垂深，m；Δρfm为所钻地层的安全密度窗口，g/cm3；ρdp为环空多相流循环压耗的当量密度，g/cm3。

2013年，考虑环空岩屑浓度、安全余量及环空波动压力等参数的影响，分别建立了破岩、管柱上提和下放时的大位移井钻井裸眼延伸极限预测模型，使预测结果更符合实际工况[42-43]，并取三者最小值作为许用值。其中，破岩钻进过程中裸眼延伸极限预测模型为：

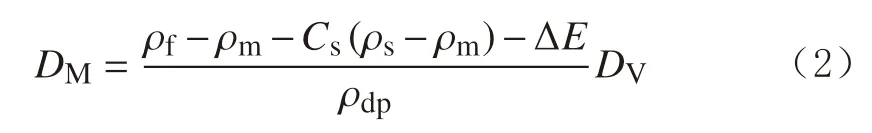
式中：ρf为地层破裂压力当量密度，g/cm3；ρm为钻井液密度，g/cm3；ρs为岩屑密度，g/cm3；Cs为环空岩屑浓度；ΔE为安全余量，g/cm3。

2016年，基于上述预测模型，笔者通过引入水平段环空多相流循环压耗梯度，得到了大位移水平井水平段裸眼延伸极限和井深延伸极限的预测模型[44-46]：

式中：DH为大位移水平井水平段延伸极限，m；Δpv为垂直段环空压耗，MPa；Δpdi为若干斜井段环空压耗，MPa；(Δp/ΔL)h为水平段环空压耗梯度，MPa/m；Ddi为若干斜井段井深，m。

笔者利用式（3）中的裸眼延伸极限预测模型对钻井安全密度窗口进行了修正[47]，对比了不同钻井液流变模式下大位移井钻井裸眼延伸极限的变化情况[48]，并研究了连续油管钻井裸眼延伸极限，扩展了预测模型的应用范围[49-50]。

2.2.2 大位移井钻井机械延伸极限

笔者基于机械延伸极限的定义，综合考虑地面和井下诸多约束因素的影响，并结合各种钻井作业工况，建立了旋转钻井机械延伸极限的定量预测模型，并绘制了不同井眼钻井机械延伸极限的预测图版，并以扩大钻井机械延伸极限为宗旨，提出了相应的钻井优化设计原则和方法，主要包括井眼轨道、导向钻具组合及井下减阻工具的优化设计准则，以改进常规钻井工程设计存在的不足[51-54]。大位移井钻井机械延伸极限的目标函数可表达为：

式中：L 为目标井深函数，m；L(·)通常以隐函数的形式表达，具体为井下管柱整体力学模型；p为约束参数，包括大钩载荷、转盘扭矩、钻头钻压和钻头扭矩等参数；d为设计参数，包括管柱组合、井眼轨道和减阻接头等参数；P 为约束参数p的许用空间，以约束条件的形式给出；p∗为最优约束参数，在最优约束参数下井深取得最大值；c为操作工况，包含滑动和旋转钻进模式下的管柱上提和下入作业。

式（4）的数学含义是，对于某一特定的钻井系统，在某一设计参数d 及操作工况c 下，约束参数p在其约束空间P内所能取得的井眼长度最大值。

钻井作业过程中，钻井管柱主要存在地面约束、钻头约束和管柱失效约束等3类约束条件。

1）地面约束条件。上提过程中大钩轴向拉力不能高于额定提拉载荷，下放过程中大钩载荷不小于零；钻机扭矩不高于额定扭矩。

2）钻头约束条件。钻头破岩存在门限钻压和门限扭矩，管柱上提过程中可能存在卡钻载荷。

3）管柱失效约束条件。管柱屈服强度与等效应力之比不小于所要求的安全系数，管柱磨损小于所要求的允许量等。

井下管柱轴向运动按运动方向分为上提和下放，按管柱是否旋转分成滑动和旋转，这2种分类组合形成了4种作业工况：滑动上提、滑动下放、旋转上提和旋转下放。

结合目标函数和约束条件，将每种作业工况下的机械延伸极限问题转换为约束优化问题，求解即可得到延伸极限的计算结果。滑动钻进的延伸极限为滑动上提和滑动下入的最小值；旋转钻进的延伸极限为旋转上提和旋转下入的最小值。

2.3 大位移井钻井延伸极限分布规律

对比理论计算结果[22]（见图2）和图1所示的统计资料可知，理论延伸极限（旋转钻进）与统计延伸极限具有相似规律：横向延伸极限随着井眼垂深呈现出“迅速增大—稳定—线性降低”的趋势，分别对应浅井、中深井和深井的情形。从图2可以看出，旋转钻进模式下的横向延伸极限明显高于滑动钻进模式下的横向延伸极限。

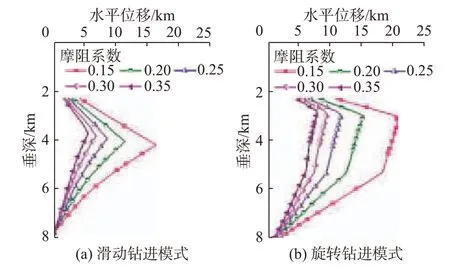
图2 不同摩阻系数下定向钻井延伸极限Fig.2 Directional drilling extension limit under different friction coefficients

利用大位移井钻井延伸极限预测模型进行分析，可得到如下规律：

1）对于浅井（稳斜角较大的定向井、水平井）而言，延伸极限对应的作业工况是管柱下入。滑动钻进时，大斜度井段管柱螺旋屈曲引起的高摩阻，是限制延伸极限的首要因素。对于水平井，单纯增大造斜点的深度对提高机械延伸极限的作用很小；对于三段式定向井，随着井斜角由90°逐渐减小，管柱的摩阻降低，导致横向延伸极限随着垂深增大而迅速增大。为了提高延伸极限，可以采取旋转导向钻进、优化稳斜角、降低摩阻系数和抑制管柱屈曲等技术措施。

2）对于深井（稳斜角较小的定向井、直井）而言，延伸极限对应的作业工况是管柱上提，限制延伸极限的主要因素是上提载荷超过大钩额定载荷或者过载导致管柱失效。随着井斜角由0°逐渐增大，管柱上提阻力与稳斜角密切相关，横向延伸极限DH随着垂深DV的增大，大致以1/µ1（µ1为平均滑动摩阻系数）的速率线性降低。为了提高延伸极限，可提升大钩额定载荷或者采用高抗拉强度管柱。

3）对于中深井（井深介于浅井和深井之间，井斜角的数值居中）而言，管柱下入或上提是延伸极限对应的作业工况，随着垂深的增大由管柱下入过渡到管柱上提。管柱上的高摩阻、管柱上提过载（超过大钩额定载荷和管柱抗拉强度）及管柱旋转过载（超过转盘额定扭矩以及管柱抗扭强度），是限制延伸极限的因素。对于滑动钻进而言，前两者起主要作用；对旋转钻进而言，管柱旋转过载不可忽略。在这些因素的综合影响下，横向延伸极限随着垂深的增大呈现出先增大后降低的趋势，且稳斜角在临界值αh=arctan(1/µ1)附近时达到横向延伸极限。为了提高机械延伸极限，首先需要利用机械延伸极限预测模型分析主要限制因素，然后从优选稳斜角、抑制管柱屈曲、降低摩阻、提高钻机性能和管柱强度等方面进行优化。

3 基于延伸极限的钻井工程设计方法

为了延长油气储层中水平段长度以提高单井产量及最终采收率，或为了钻达更远处的地下目标，需要进一步提高大位移井的延伸极限，因而需要建立基于大位移井延伸极限的钻井优化设计方法。

3.1 钻井液密度和排量优化设计方法

钻井液密度优化设计的原则：一是最优钻井液密度必须满足修正的安全密度窗口；二是大位移水平井可以在该最优钻井液密度下获得最大延伸极限。任意钻井液密度下都存在一个大位移水平井水平段延伸极限Lh(ρ)，它是该井水平段裸眼延伸极限Lh-op和水力延伸极限Lh-hy的最小值：

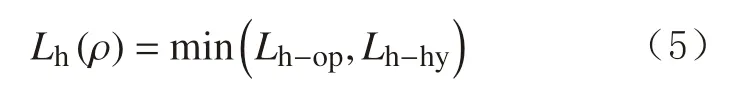
以获得最大水平段延伸极限Lhmax为目标，确定最优钻井液密度ρopt。图3列出了几种可能的情形，其中Lh-op利用式（3）得到，Lh-hy利用文献[50]中方法求解。具体步骤如下：

图3 不同情形下的水平段延伸极限Fig.3 Horizontal extending limits in different cases

1）若Lh-op曲线和Lh-hy曲线有交点（见图3（a）），则交点的X轴坐标值为最优钻井液密度ρopt，交点的Y轴坐标值为水平段延伸极限的最大值Lhmax。

2）若Lh-op曲线和Lh-hy曲线无交点且Lh-hy一直大于Lh-op（见图3（b）），则Lh-hy的最大值为水平段延伸极限的最大值Lhmax，该点的X轴坐标值为最优钻井液密度ρopt。

3）若Lh-op曲线和Lh-hy曲线无交点且Lh-op一直大于Lh-hy（见图3（c）），则Lh-op最大值为水平段延伸极限的最大值Lhmax，该点的X轴坐标值为最优钻井液密度ρopt。

4）若Lh-op曲线和Lh-hy曲线无交点（见图3（d）），且任意钻井液密度下Lh-op为零或Lh-hy为零，则钻井液安全密度窗口不存在，不存在最优钻井液密度ρopt。

最优排量和最优钻井液密度的设计方法基本相同，只是将式（6）—式（9）中的ρ替换为Q即可。

3.2 大位移井管柱优化设计方法

笔者提出了一种将大位移井分成下部大斜度井段和上部常规井段进行管柱优化设计的方法。下部大斜度井段的井斜角比较大，水平延伸距离长，裸眼段长，因此钻进该井段时管柱高摩阻和高扭矩问题比较突出，是限制大位移井延伸极限的主要原因。同时，大斜度井段穿过油气储层，对固井质量要求高，因此设计目标中需要包含套管居中度约束。为此，采用加权目标函数的方法，目标函数中包括摩阻、扭矩和套管居中度等参数，其计算公式为：

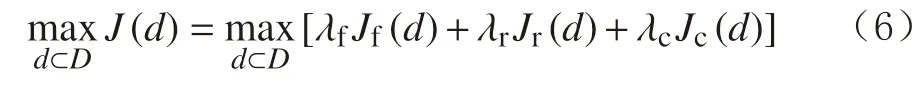
式中：J 为总目标函数；Jf，Jr和Jc为与管柱摩阻扭矩、套管居中度及成本相关的子目标函数；λf，λr和λc为相应的权重系数；d为设计参数。

式（6）可采用先局部后整体的方法进行求解[52]。其计算思路为：1）将大斜度井段的管柱分成若干局部井段；2）从靠近钻头的局部井段进行优化设计，得到该井段管柱的最优设计参数；3）沿着井深减小的方向依次对各个局部井段进行优化设计；4）综合各个局部井段的设计参数，得到大斜度井段管柱的整体最优设计结果。

上部常规井段与常规定向井的井眼轨迹参数类似，但下部大斜度井段的存在导致上部常规井段管柱受力状况更加复杂，因此常规定向井管柱设计方法难以满足大位移井上部常规井段的要求。为了同时考虑各种作业工况，可采用延伸极限作为目标函数，即[52]：

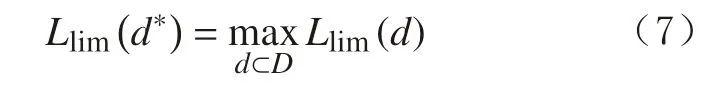
式中：d*为最优设计参数；Llim为井眼延伸极限，m，利用式（4）计算。

通常而言，方程的求解耗时比较长，可采用延伸极限的近似求解公式作为目标函数进行计算[52]。

4 应用实例

萨哈林地区Z-42井创造了井深（12 700 m）最深和水平位移（11 739 m）最长的世界纪录[19]，其垂深为2 338 m，水垂比高达5.02，属于高难度大位移水平井，其设计井眼轨道如图4所示。该井采用四开井身结构，水平段长度约为3 500 m，完井周期约为70 d。分析Z-42井施工报告可知，四开裸眼段钻进过程中的高扭矩和完井筛管在裸眼水平段内滑动下入的高摩阻是限制该井水平延伸的2个重要因素。针对这2种工况，利用本文的理论模型，分析不同技术措施对提高延伸极限的作用。

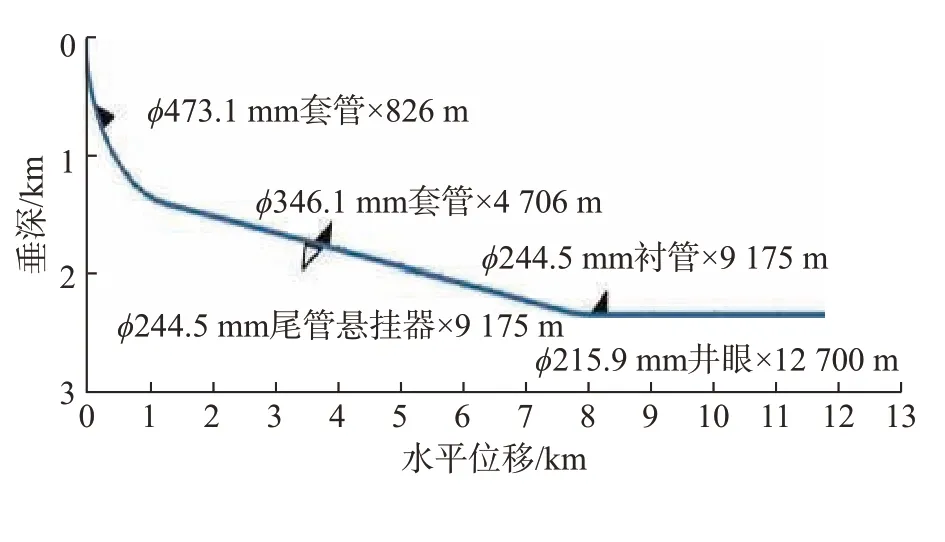
图4 Z-42井设计井眼轨道Fig.4 Designed wellbore trajectory of Well Z-42

4.1 水平段旋转钻进极限分析

Z-42井四开φ215.9 mm水平段应用旋转导向工具钻进，钻具组合中包括φ149.2 mm加重钻杆和普通钻杆、φ168.3 mm钻杆等。其中，φ149.2 mm钻杆的上扣扭矩为96 kN·m，φ168.3 mm钻杆的上扣扭矩为108 kN·m，钻机额定扭矩为95 kN·m，可见，钻机额定扭矩是限制φ215.9 mm井眼延伸极限的主要因素，因此，提升钻机性能是提高井眼延伸极限的可行措施之一。利用式（4）进行计算，得到了不同钻机额定扭矩和摩阻系数下的井眼延伸极限（见图5）。由图5可以看出，在相同摩阻系数下，提升钻机性能可大幅度提高井眼延伸极限，能满足该井井深12 700 m的钻井需求。

图5 不同额定扭矩和摩阻系数下的井眼延伸极限Fig.5 Wellbore extension limit at different rated torques and friction coefficients

4.2 完井管柱下入极限分析

Z-42井完井管柱主要包括1 499 m的φ168.3 mm筛管和2 149 m的φ139.7 mm筛管，筛管上部与钻柱连接，采用滑动方式下入。完井管柱在超长套管段和裸眼段内将产生高摩阻，导致下入困难。为此，该井完井作业时在筛管与钻柱之间安装了旋转接头，保证管柱下入过程中上部钻柱处于旋转状态，而下部筛管处于不旋转状态，从而大幅度降低管柱在套管段的摩阻及筛管下入作业难度。

利用式（4）进行计算，得到了安装和不安装旋转接头、安装和不安装减阻接头条件下的完井管柱延伸极限（见图6）。由图6可以看出，如果摩阻系数偏大且不安装旋转接头，完井管柱将无法下至井底；安装旋转接头可明显改善井下管柱的受力状况，完井管柱可顺利下到井底；同时安装旋转接头和减阻接头，可进一步提高完井管柱的下入极限。

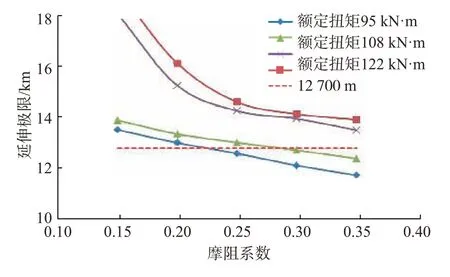
图6 完井管柱旋转和滑动下入极限Fig.6 Entry limits of completion string in rotary and sliding RIH modes

5 结束语

大位移井广泛应用于海洋、滩海、湖泊及山地等复杂地区油气资源的高效开发，相关的科技进步与工程实践在国内外备受关注。大位移井钻井延伸极限预测和控制与相应的技术、装备、作业环境及作业参数等诸多因素密切相关，是一个复杂的约束优化问题，需要不断加强研究与实践。显然，大位移井钻井延伸极限并不是固定值，将随着大位移定向钻井技术与装备的创新发展而不断提高。开展大位移井钻井延伸极限理论研究，力求实现工程作业极限的定量预测分析，揭示限制作业极限的主要因素及其影响规律，以便为工程作业的风险分析、优化设计及安全控制提供科学依据。