A电商物流中心三维装箱作业优化设计

2019-06-28陈增坤

物流工程与管理 2019年6期

关键词：箱型装箱包装箱

□ 余蕾，王旭，陈增坤

(青岛理工大学管理工程学院，山东青岛 266520)

1 A电商物流中心基本情况

A电商物流中心在其小件商品打包环节中，系统依据订单商品总体积与纸箱容积之间的模糊关系自动推荐的打包纸箱通常是不准确的，需要打包员判断并重新选择纸箱，在这个过程中造成了纸箱的浪费，大大增加了作业成本。

A电商物流中心中每一订单涉及到的商品基本在2～6项之间，货物数量少且不涉及装卸搬运问题，约束条件较简单，但不规则货物占比较大，由于不规则货物的装箱问题极其复杂，因此，本文在尽量减小影响的情况下将不规则的物品填充成规则的形状进行讨论。

本文采用填充率最大作为衡量打包纸箱匹配程度的标准，运用改进的砌墙算法，将原本单一的参考线扩充为以物流中心五种固定规格包装箱尺寸为标准的多条参考线，运用迭代计算得到最经济合理的包装箱。

2 基本假设

三维装箱问题的关键在于针对不同的约束条件和装载目标函数，构建相应的装箱问题模型，根据装箱问题模型设计优化算法，从而完成三维装箱问题的优化求解。本文采用改进的砌墙算法进行求解，在构建装箱模型之前，作如下假设：

①所有货物的外形看作规则的长方体。

一般来说，货物可以是任意规则或不规则的形状，目前国内外研究三维装箱课题主要研究的是具有规则形状的装箱问题，A电商物流中心涉及到的商品主要为零散货物，商品形状多样，为避免问题过分复杂化，理论计算时，我们选取商品的长宽高信息，将其统一填充成规则的直方体进行讨论，易得，填充后的商品体积必定大于未填充的商品，因此，当根据填充货物体积进行计算从而选择的包装箱能够满足要求时，则必定能满足原货物的打包要求。

②所有货物具有良好的外包装强度，其承重能力足够大。

③所有货物平行或正交于包装盒盒体表面放置。

④货物被打包时，其表面平行于包装纸箱的底面和四壁。

⑤可忽略货物本身的挤压变形。

⑥在打包过程中，放入打包纸箱的货物可以向下、向前、向左移动，直到它的底面、前面、左面与其它货物或是包装箱相邻。

3 基于改进的砌墙算法的三维装箱打包模型

拟人的思想在解决实际问题时是很有效的，在日常砌墙时，人们一般会先放置一块参考砖，并以参考砖的高度作为基准，规定每个物品的高度都不能超过参考砖的高度，当物体不能放入时，则提高参考砖的高度，受此思想的启发，我们在三维装箱过程中，在水平和垂直方向上同时引入参考线来引导装填过程。

如图1所示，本模型采用三维笛卡尔坐标系建立包装箱箱内空间模型，坐标系的XYZ三个坐标轴分别对应打包纸箱的长度方向、宽度方向、高度方向，坐标系原点表示打包纸箱的左后下角。

图1 包装箱三维坐标系

我们考虑两条参考线，Z轴上的参考线Lz与Y轴上的参考线Lx，在进行货物摆放的过程中，要求其不能与纸箱或其他货物相交，在检测一个可放置位置时，尝试所有的可放置方向，若所有可放置点都不能放入该箱子，则同时提高Z轴与X轴的参考线，再进行一次遍历搜索摆放顺序，当参考线提升至参考线5时，若仍不能放下，则在此次装填中，该订单内的货物不能放入一个包装箱中。出现这种情况时，代表一个订单货物须分成至少两个包装箱进行出库。经过对A物流中心的现状分析，我们发现其不同于传统三维装箱问题，属于Open Dimension Problem(ODP):货物装入单个尺寸不定容器问题，ODP问题比较特殊容器的尺寸是不确定的，将一定数量的货物用矩形箱体包装，使包装箱体容积最小。A电商物流中心的包装箱规格表如表1所示：

表1 包装箱规格表

图2 水平参考线图3 垂直参考线

因此，选用Z5规格作为初始规格包装箱进行比较，以Z1～Z4规格作为参考线1～4，在进行装箱时，以参考线1作为第一条参考线，进行迭代，直至迭代至Z5规格，若Z5规格仍无法满足装箱要求，则需用至少两个包装箱。

4 打包方案实例验证

4.1 打包规则

依据A电商物流中心的规定，其商品打包过程中需遵守以下打包原则：

①化学用剂类(洗发水、香皂、肥皂、洗衣粉、各类清洁剂、杀虫剂)不可与食品类混装。

②电子产品类(剃须刀、电动牙刷等电子类产品)独立打包出库，不可与其他商品混装。

③液体类商品不可与其他商品混装。

④纺织类(床单、枕头、棉被、衣物等)一般不与食品类商品混装，避免污染。

⑤单箱限装15件，包裹重量不超过8kg。

4.2 打包方案实例验证

我们从A电商物流中心系统数据中选取了1个较为典型的订单进行验证，订单中的商品数据如表2所示。

表2 某次订单中的商品数据

在此订单中，包括液体与食品两类商品。液体类商品包括6件“张裕葡萄酒礼盒”和1件“五粮液(福禄寿喜)”，由于存在纸箱中商品总重量不能超过8kg的装箱原则，且液体类商品的总体积超过了纸箱的最大容积，所以液体类商品不能放入同一个箱子中。于是将液体类商品分成两个纸箱进行打包，5件“张裕葡萄酒礼盒”一起打包，总体积为31360cm3，总重量为7.5kg，按照体积应选择纸箱Z5；1件“五粮液(福禄寿喜)”和1件“张裕葡萄酒礼盒”一起打包，总体积为12572cm3，总重量为2kg，按照体积应选择纸箱Z3。食品类商品共包括6件“威士雅金丝燕窝”，总体积为60000cm3，超过了最大箱子的容积，所以将6件“威士雅金丝燕窝”分为每三件一起打包，按照体积应选用纸箱Z5，共使用两个。参照系统中的选箱原则，打包最终方案如表3所示。

表3 按照系统中的选箱原则制定打包方案

由于商品的形状限制，单纯按照体积的对应原则选择纸箱是很不准确的，上表中对纸箱的选择并不完全合适，由于商品长宽高的限制，无法完成打包出库作业。经过算法计算，将选箱方案调整如表4所示，“张裕葡萄酒礼盒”需要用两个Z5纸箱打包，每箱装三件；“五粮液(福禄寿喜)”需要用一个Z3纸箱打包；“威士雅金丝燕窝”需要用三个Z4纸箱打包，每箱装两件。具体的装箱方案示意图如图4、图5、图6所示。

表4 按照拟人式砌墙算法得到的装箱打包方案

图4 “张裕葡萄酒礼盒”装箱方案示意图

图5 “五粮液(福禄寿喜)”装箱方案示意图

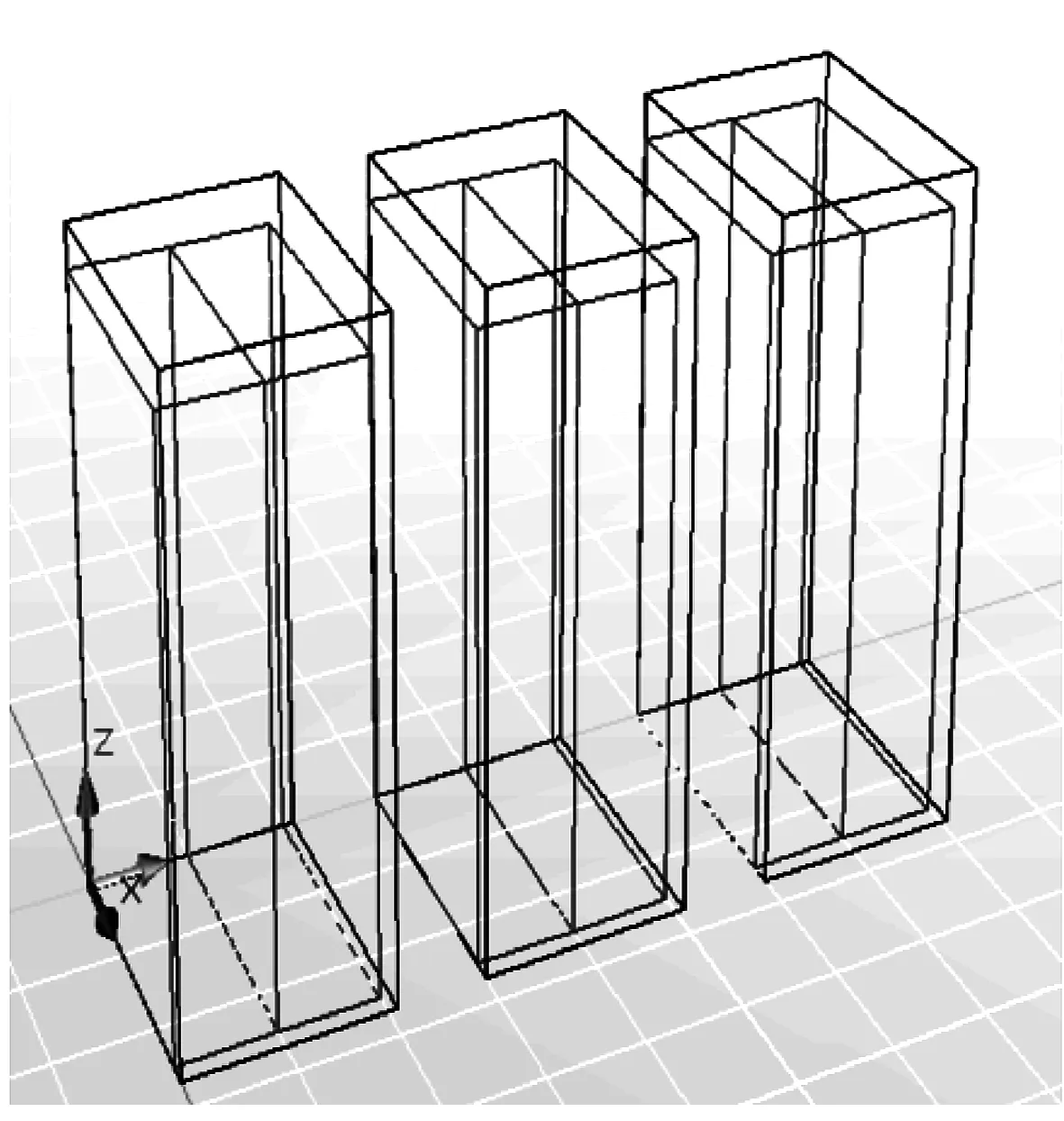
图6 “威士雅金丝燕窝”装箱方案示意图

5 成本分析

5.1 额外成本的产生

系统原本的选箱原则为模糊的体积对应原则，即计算出订单中商品的总体积之后，在五种规格的纸箱中满足体积大于或等于商品总体积的所有箱型中选择一个容积最小的纸箱进行打包。但是由于商品和纸箱形状的限制，在装箱过程中不可避免的会产生不可利用空间，实际商品所需的总容积往往大于商品的总体积，所以利用这种方法只能初步筛选出一个待尝试进行装箱的纸箱，该纸箱可能会不完全合适。当出现这种情况时，要依次更换更大的纸箱进行尝试装箱，若最大的纸箱都无法满足打包要求时，再将商品分批用多个纸箱进行打包，直到将所有商品都完全打包为止。这样的方法会产生额外的纸箱成本与时间成本，造成打包的浪费。

5.2 成本的降低

在利用本方案进行选箱时，会充分结合商品和纸箱的长、宽、高进行组合优化，在将商品放到打包纸箱的过程中，不断利用参考线进行最佳打包纸箱的选择，一次性产生较优的装箱方案，避免了打包员在实际打包过程中发现所选箱型不合适时重新进行选箱，从而减少了纸箱的浪费，节约了装箱打包成本。

6 存在的问题

在制定装箱打包方案时，我们发现了系统打包过程中存在的一些问题，导致纸箱的利用率比较低，以下是对存在的问题以及改进方法的总结：

6.1 箱型较少

在利用本文算法实现装箱的过程中，我们发现由于A电商物流中心的箱型较少，且箱型的分配存在不合理之处，比如一件“张裕葡萄酒礼盒”的总体积为6272cm3，纸箱Z3容积为3000cm3，Z4容积为15000cm3，由于Z3与Z4的容积差距太过悬殊，而Z3和Z4之间又缺少其他可选择的箱型，所以只能选择容积较商品体积过大的纸箱Z4，导致纸箱的容积利用率只有41.8%，从而造成纸箱浪费，成本过高。

针对这种情况，可以适当在不同类型的纸箱之间增加中间箱型，如容积为9000cm3、19000cm3、29000cm3,的纸箱，以便在装箱打包的过程中有更多的箱型可以选择，尽可能的降低纸箱成本。