空间曲线平移并联机构构型综合与分类

叶梅燕 石志新 罗玉峰,3

(1.南昌大学机电工程学院， 南昌 330031； 2.南昌大学理学院， 南昌 330031；3.华东交通大学机电与车辆工程学院， 南昌 330013)

0 引言

在管道焊接、曲面加工、轨迹追踪等工程应用中，人们通常期望设计出执行构件能够沿空间曲线运动的机械装备。目前人们的设计思路大多基于外在几何观点(将空间曲线嵌入外围3维欧氏空间)，即设计一个三平移机构，通过算法协调控制3个方向的移动输出，实现执行构件沿指定空间曲线作平移运动。然而根据高斯非欧几何的内蕴思想(将曲线和曲面本身视为独立空间)，空间曲线属于1维几何形体，若采用1自由度的曲线平移机构替代上述三平移机构，则可实现减少自由度、降低控制难度、节约成本的目的。因此，研究简单、实用的各类曲线平移机构十分必要。

目前机器人机构构型综合的方法主要有：基于螺旋理论的方法[1-6]、基于位移子群/流形的运动综合方法[7-11]、基于线性变换与进化形态学的方法[12-13]、基于方位特征集的方法[14-20]以及基于GF集的综合方法[21-24]。然而，这些理论方法均难以直接应用于具有弯曲平移(沿曲线或曲面平移)运动特征的机构，原因为：①缺少可描述弯曲平移运动特征的表达模型。②过于强调局部运动特征，缺少平移空间整体形态特征。③缺少弯曲平移运动特征的运算规则。对于弯曲平移机构而言，由于移动方向时刻变化，因此局部运动特征不能反映整体形态特征，而且基于线性空间的运动特征求交和求并运算规则不再适用。

本文根据内蕴几何思想，建立可描述弯曲平移运动特征的表达模型，研究机器人机构末端构件弯曲平移运动的形成机理及其基本类型，制定弯曲平移运动特征的运算规则，并结合实例提出空间曲线平移并联机构的构型综合方法。

1 可描述弯曲平移运动特征的表达模型

刚体运动包括平移和转动2种基本运动类型，因此机器人末端构件的运动特征应由平移特征和转动特征共同组成。

(1)旋转特征。转动特征可由旋转轴数量和方向来表征。

(2)平移特征。平移运动包括平直移动(沿直线或平面平移)和弯曲平移(沿曲线或曲面平移)2种情况。如平行四边形机构的连杆作圆周曲线平移运动，3-UU机构[21]的动平台沿球面作平移运动等。由于弯曲平移的移动方向时刻变化，因此其运动特征需要由平移空间的维数、整体形态以及生成方式三者共同表达。

综合考虑旋转特征和平移特征，本文采用的末端构件运动特征描述模型为

(1)

式中M——末端构件的运动特征集

t——平移

p——平移空间的维数(独立平移数目)

w——平移空间的整体形态

N——平移空间的生成方式

r——转动

q——独立旋转方向矢量的数目

S——旋转轴方向单位矢量组成的集合

基于内蕴几何学的基本思想，直线和曲线可被视为1维独立平移空间，平面和曲面则被视为2维独立平移空间。0维和3维平移空间无需记录整体形态和生成方式，故其移动特征可分别表示为t0和t3。0维和3维转动空间无需记录旋转轴方向，其转动特征分别表示为r0和r3。1维和2维转动空间的转动特征分别表示为r1(l)和r2(l1,l2)，其中l、l1和l2均为旋转轴方向的单位矢量。

2 支链末端构件弯曲平移运动的形成

由于支链(串联机构)是由若干个运动副依次串联而成，因此其末端构件的运动特征集是各运动副运动输出特征的并集，可表示为

(2)

式中ML——支链末端构件的运动特征集

2.1 单自由度运动副的运动输出特征

机器人机构的运动副类型较多，常见运动副包括：转动副(R副)、移动副(P副)、球副(S副)、胡克铰(U副)、圆柱副(C副)等。为了分析方便，可采用运动副等效替换的方法将它们简化为只含转动副和移动副。如球副等效为3个轴线汇交于1点的转动副，胡克铰等效为2个轴线垂直正交的转动副，圆柱副等效为共轴的转动副和移动副。

(1)P副的运动输出特征。由于P副仅产生直线平移运动，其移动空间整体形态为直线，并且该移动空间由P副生成，由式(1)可知，移动副的运动输出特征可表示为t1(直线,P)，其中P为P副方向的单位矢量。

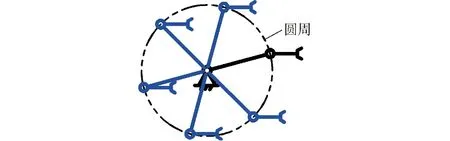
图1 R‖R机构及其末端构件的平移空间Fig.1 R‖R mechanism and translation space of its end-effector

(2)R副的运动输出特征。转动副不仅能产生绕其轴线的运动，而且可衍生出垂直于轴线方向的圆周曲线平移运动，即其运动特征具有二重性，可按如下规则选取：①优先取旋转运动作为运动输出特征，记为r1(R)，其中R为R副轴线方向的单位矢量。②若已有运动副产生了与该转动副旋转方向相同的旋转运动，则该转动副将会衍生圆周曲线平移(图1)，此时应取衍生圆周曲线平移作为其运动输出特征，记为t1(圆,R┴)，其中R┴表示由R副衍生且与R垂直的圆周平移运动。

2.2 2维曲面平移运动的形成及其类型

2维曲面平移空间是由2个1维平移空间合并而成，而且二者不能均为直线，即其中至少1个1维平移空间应为圆周。

2.2.1t1(直线)与t1(圆)的求并运算规则

由2.1节可知，1维圆周平移空间存在2种生成方式：一种由Pa副产生，另一种为两平行R副衍生而成。

高校的课程设置不仅决定一个专业的定位，决定专业的宽度和广度，更决定未来所培养学生的视野、知识储备、专业倾向等综合素质，是高校办学中非常重要的环节。地方本科高校无论历史沉淀、师资力量、学生素质还是整体综合实力，与综合性大学相比，差距都是非常大的。在这种情况下，扎根当地，发掘能够体现地方价值与特色的课程就显得尤为重要。

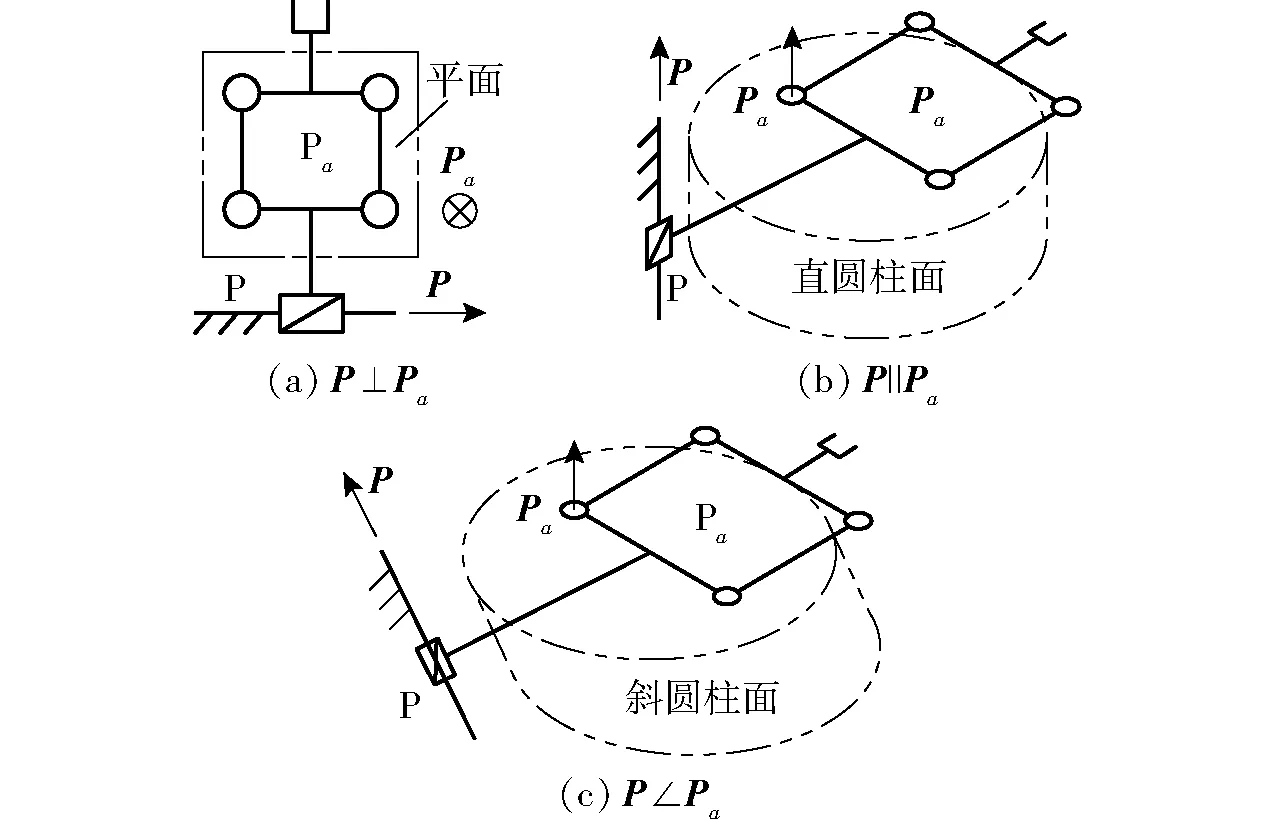
图2 P-Pa机构及其末端构件的平移空间Fig.2 P-Pa mechanisms and translation spaces of theirs end-effector

(2)当1维圆周平移空间由两平行R副衍生而成时，P副与它们在各种装配关系下的合成2维平移空间如图3所示，因此t1(直线,P)与t1(圆,R┴)的求并结果如下：

当P⊥R时，二者合成的平移空间为平面(图3a)，故此时t1(直线,P)与t1(圆,R┴)的求并结果记为t2(平面,R)。

当P‖R时，二者合成的平移空间为直圆柱面(图3b)，故此时t1(直线,P)与t1(圆,R┴)的求并结果为t2(直圆柱面,P⊕R┴)。

当P∠R且P副位于两平行R副两边时，二者合成的平移空间为斜圆柱面(图3c)，故此时t1(直线,P)∪t1(圆,R┴)=t2(斜圆柱面,P⊕R┴)。

当P∠R且P副位于两平行R副中间时，二者合成的平移空间为圆锥面(图3d)，故此时t1(直线,P)∪t1(圆,R┴)=t2(圆锥面,P⊕R┴)。

RPR机构(图3)的末端构件除了具有2维平移特征外还具有绕R旋转的1维转动特征。

图3 RPR机构及其末端构件的平移空间Fig.3 RPR mechanisms and translation spaces of theirs end-effector

2.2.2t1(圆)与t1(圆)的求并运算规则

两圆周平移存在3种生成方式：两圆周平移均由Pa副产生、两圆周平移均由R副产生、两圆周平移分别由Pa副和R副产生。由于上述3种生成方式下的合成平移空间类型均相同，因此无需分别讨论。

两圆所在的平面存在平行、相交(包括垂直和斜交)2种位置关系，且两圆心的位置存在重合与不重合2种情况。上述各种方位关系对应的机构示例如图4所示。

图4 两圆周平移合成各类2维空间的实例Fig.4 Examples of 2-dimension space generated by two circular-translation motion

综合上述分析结果可以得出，支链末端构件的2维曲面平移空间存在圆柱面(包括直圆柱面和斜圆柱面)、圆锥面、球面、环面这4种基本类型。

3 空间曲线平移并联机构的构型综合

3.1 空间曲线平移并联机构的基本类型

并联机构由静平台(机架)、动平台以及若干条支链组成。由于动平台是在各支链共同作用下进行运动，因此其运动特征是各支链末端构件运动特征的交集。又考虑到空间曲线可看作空间两曲面的交线，因此空间曲线平移并联机构可由2条具有2维弯曲平移运动特征的支链构成。

根据第2节分析结果可知，支链末端构件的2维曲面平移空间存在4种形态(圆柱面、圆锥面、球面、环面)。考虑到这些曲面两两的交集一般为1条空间曲线(称为相贯线)，因此空间曲线平移并联机构可按曲线形态划分为9种基本类型：柱柱相贯线平移机构、柱锥相贯线平移机构、柱球相贯线平移机构、柱环相贯线平移机构、锥锥相贯线平移机构、锥球相贯线平移机构、锥环相贯线平移机构、球环相贯线平移机构和环环相贯线平移机构。两球面的交线为圆(属于平面曲线)，它不属于空间曲线。

本文仅对上述9种基本类型中的前2类并联机构进行构型综合，其余7类机构可以采用类似方法综合得到。

3.2 柱柱相贯线平移机构构型综合

3.2.1具有2维圆柱面平移特征的支链

根据2.2.1节分析结果可知，2维圆柱面平移空间由直线平移和圆周平移合成产生，并且直线和圆所在的平面不能平行。具有2维圆柱面平移特征的支链结构类型如表1所示。

表1 具有2维圆柱面平移特征的支链
Tab.1 Branches with 2-dimension cylindertranslation characteristic

3.2.2支链组合方案

根据3.1节分析结果可知，柱柱相贯线平移机构可由表1中某2条支链(记为支链1和支链2)构成。为保证动平台沿柱柱相贯线作纯平移运动(不含转动)，支链1、2的组合方案如表2所示。

表2 柱柱相贯线平移机构支链组合方案Tab.2 Branch assembling schemes of cylinder-cylinder intersection line translation mechanisms

3.2.3支链装配几何条件

(1)t2(圆柱面)与t2(圆柱面)的求交运算规则

当两圆柱面的轴线平行时，二者的交线为平行于轴线的直线；否则，二者的交线为空间曲线(柱柱相贯线)。因此，2维弯曲平移特征t2(圆柱面)与t2(圆柱面)的求交运算规则为

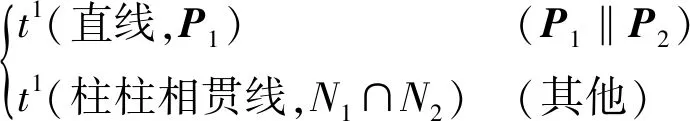
(3)

(2)两支链装配几何条件分析

根据预期设计目标，支链1和支链2的运动特征集应满足

(4)

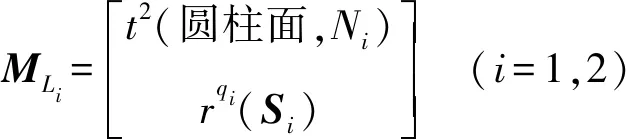
式中qi——支链i末端构件旋转方向矢量的数目

Si——支链i末端构件旋转方向单位矢量组成的集合

结合式(3)，可知式(4)成立的条件为P1与P2不平行且S1∩S2=∅(空集)。因此表2中各组合方案对应装配条件如下：

(1)组合方案1～4。支链1、2分别为表1中支链结构类型库A0和Ai(i=0,1,2,3)。由于支链1的转动特征为r0(表1)，故此时S1∩S2=∅恒成立，因此支链1、2的装配条件为P1与P2不平行。

(2)组合方案5。支链1、2均为表1中支链结构类型库A1，二者的转动特征可分别记为r1(R1)和r1(R2)。此时S1∩S2=∅成立的充要条件为R1与R2不平行，因此支链1、2的装配条件为P1与P2不平行且R1与R2不平行。

(3)组合方案6。支链1、2分别为支链结构类型库A1和A2，二者转动特征分别为r1(R)和r1(R1,R2)(表1)。此时S1∩S2=∅成立的条件为R与R1、R2均不平行，故支链1、2的装配条件为P1与P2不平行且R与R1、R2均不平行。

3.2.4柱柱相贯线平移机构

根据上述支链组合方案和装配几何条件，可综合得到25种柱柱相贯线平移机构。表2中组合方案1～6生成的代表性机构如图5所示。

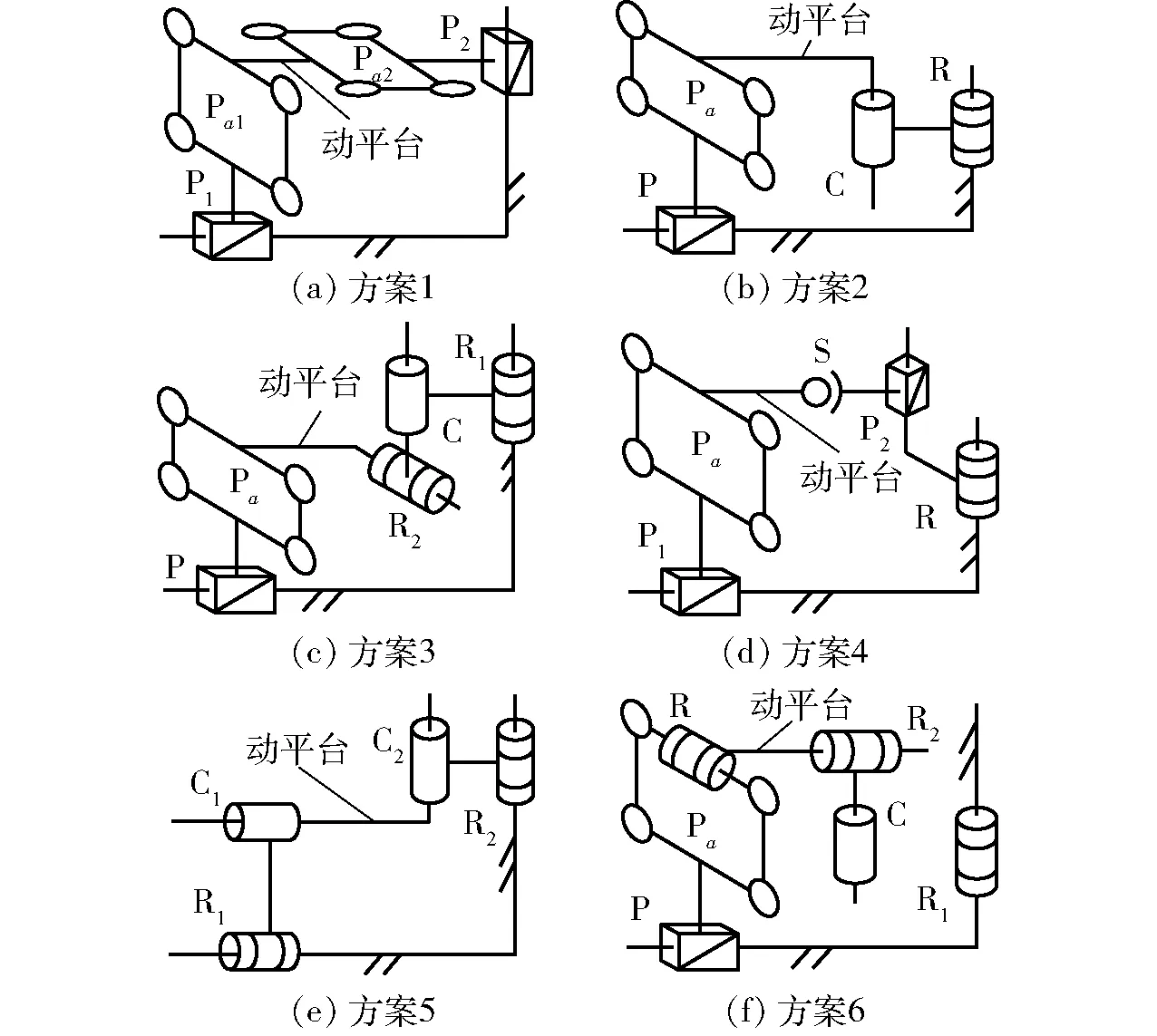
图5 表2各组合方案生成的代表性并联机构Fig.5 Representative mechanisms generated by assembling schemes in Tab.2

3.2.5分析验证

以图5e所示机构为例，分析该机构动平台的运动特征。

已知两支链末端构件运动特征集为

其中Pi为圆柱副Ci轴线方向单位矢量。故二者的并集为

(5)

根据自由度计算公式[14]可知，该机构自由度为

式中fi——第i个运动副的自由度

dim——维数函数

由于R1与R2不平行，r1(R1)∩r1(R2)=r0，故该机构的动平台不含转动输出，又由于自由度F等于1，因此该机构的动平台仅沿两圆柱相贯线作弯曲平移运动(图6)。

图6 R‖C-C‖R机构及其动平台的平移空间Fig.6 R‖C-C‖R mechanism and translation space of its end-effector

3.3 柱锥相贯线平移机构构型综合

3.3.1具有2维圆锥面平移特征的支链

根据2.2.1节分析结果可知，2维圆锥面平移空间产生的条件为P副位于两平行R副中间且P∠R。因此，具有2维圆锥面平移特征的支链结构类型如表3所示。

3.3.2支链组合方案

根据3.1节分析结果可知，可从表1、3中分别挑选1条支链(记为支链1和支链2)，二者共同构成柱锥相贯线平移机构。为保证动平台仅沿柱锥相贯线作纯平移运动(不含转动)，支链1、2的组合方案如表4所示。

3.3.3支链装配几何条件

为保证动平台无转动输出，两支链末端构件转动特征集的交集应为空集(即S1∩S2=∅)，因此表4中各组合方案对应装配条件如下：

(1)组合方案1～3。支链1均取自表1中支链结构类型库A0。由于支链1的转动特征为r0，故此时S1∩S2=∅恒成立，因此支链1、2可任意装配。

表3 具有2维圆锥面平移特征的支链
Tab.3 Branches with 2-dimension conetranslation characteristic

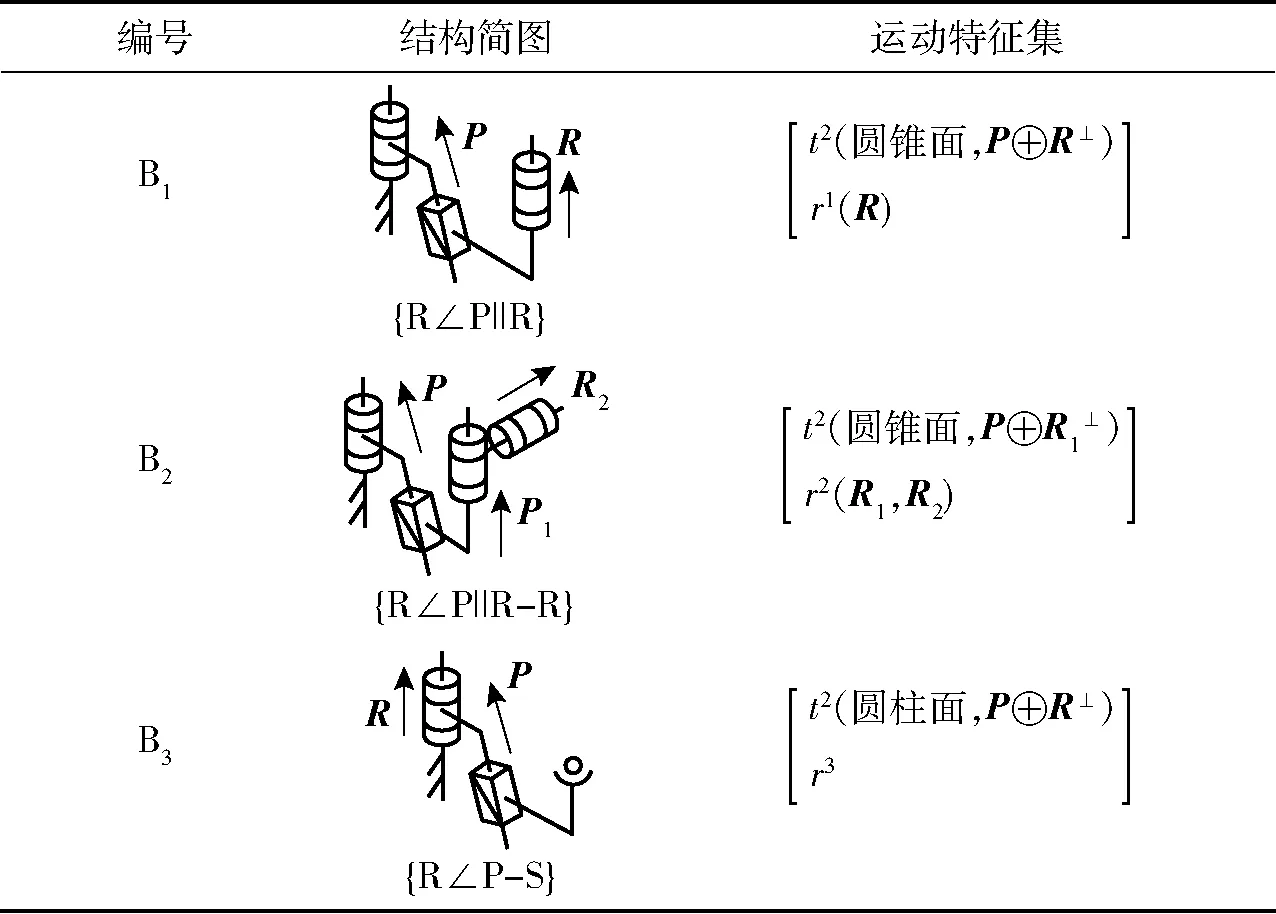
表4 柱锥相贯线平移机构支链组合方案Tab.4 Branch assembling schemes of cylinder-cone intersection line translation mechanisms

方案支链来源支链组合方案1(A0,B1){P-Pa}{R(∠P)‖R}2(A0,B2){P-Pa}{R(∠P)‖R-R}3(A0,B3){P-Pa}{R∠P-S}4(A1,B1){P-Pa-R}{R(∠P)‖R}{P‖R‖R}{R(∠P)‖R}{R‖C}{R(∠P)‖R}5(A2,B1){P-Pa-R-R}{R(∠P)‖R}{P‖R‖R-R}{R(∠P)‖R}{R‖C-R}{R(∠P)‖R}6(A1,B2){P-Pa-R}{R(∠P)‖R-R}{P‖R‖R}{R(∠P)‖R-R}{R‖C}{R(∠P)‖R-R}

(2)组合方案4。支链1取自表1中类型库A1，支链2取自表4中类型库B1，二者的转动特征分别记为r1(R1)和r1(R2)。此时S1∩S2=∅成立的充要条件为R1与R2不平行，因此支链1、2的装配条件为R1与R2不平行。

(3)组合方案5和6。支链1、2分别取自类型库A2和B1(或A1和B2)，二者的转动特征可分别记为r1(R1,R2)和r1(R)，此时S1∩S2=∅成立的条件为R与R1、R2均不平行。因此支链1、2的装配条件为R与R1、R2均不平行。

3.3.4柱锥相贯线平移机构

根据3.3.2节得到的支链组合方案和装配几何条件，共可综合得12种柱锥相贯线平移机构。图7仅列举了表4中各组合方案生成的部分代表性机构。根据自由度计算公式可计算得出，该类机构自由度为1。又由于两支链末端构件转动特征集的交集为空集，因此动平台不含转动输出，仅能沿柱锥相贯线作平移运动。

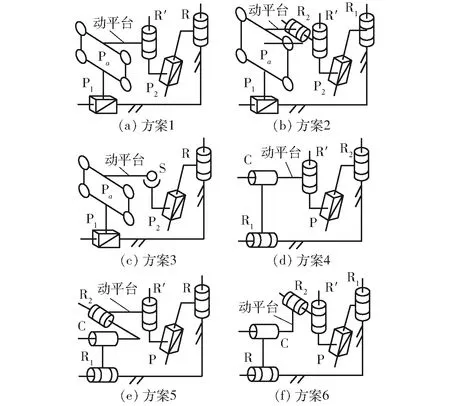
图7 表4各组合方案生成的代表性并联机构Fig.7 Representative mechanisms generated by assembling schemes in Tab.4

4 结论

(1)基于高斯非欧几何的内蕴思想，可将曲线和曲面本身视为弯曲平移空间。这些空间的维数、整体形态以及生成方式能够清晰表达末端构件的弯曲平移运动特征。

(2)支链末端构件的2维弯曲平移空间存在圆柱面(包括直圆柱面和斜圆柱面)、圆锥面、球面、环面4种基本类型。

(3)根据平移空间的整体形态，空间曲线平移机构可被划分为9种基本类型。类型细分不仅能够丰富和完善现有机构类型库，而且有利于设计者根据实际工况作出合理选择。

(4)综合得到了25种柱柱相贯线平移机构和12种柱锥相贯线平移机构，并给出了代表性机构。与三平移机构相比，这些空间曲线平移机构具有自由度小(等于1)、结构简单、控制容易等特点。