基于功率密度的大功率拖拉机变速箱壳体疲劳分析

2019-06-27温昌凯杨子涵董乃希宋正河

农业机械学报 2019年6期

温昌凯谢斌杨子涵董乃希宋正河

(中国农业大学工学院，北京 100083)

0 引言

为保证农业装备具有持续、正常的田间作业能力，结合其作业特点和实际受载情况，对其关键零部件进行准确的疲劳寿命分析与可靠性分析很有必要。变速箱是拖拉机传动系统的关键组成部分，作为安装齿轮、保护齿轮传动、支撑轴系以及储存润滑液的主要部件，是保证齿轮传动可靠、安全和准确的基础[1]。因此，有必要对其进行符合实际的疲劳寿命分析。

目前，国内有关农机装备可靠性和疲劳分析方面的研究较多。前期研究主要通过仿真得到传动系关键零部件的应力集中位置、疲劳损伤热点、应力大小以及相应的固有频率、固有振型等基本信息，从而对传动系关键零部件的改进提出了一些建议[2-5]。这些研究只是基于静态载荷的作用，无法最大限度地还原实际受载情况。近年来，相关研究开始着重讨论动态载荷等因素对传动系关键零部件的影响。郑建强[6]和裴滨[7]利用M+P Analyzer 动态分析系统和力锤激励，对变速箱壳体以及驱动桥壳进行自由模态试验，并将试验数据与有限元分析结果进行了对比验证。张立香等[8]将载荷定义为符合高斯分布的随机变量，考虑了设计变量的随机性对结构疲劳可靠性的影响。

在疲劳寿命分析领域，最常用的疲劳分析方法是名义应力法(S-N)、局部应变法(E-N)、损伤容限分析法等[9]。这些方法多以疲劳累计损伤理论为基础，疲劳累计损伤理论主要包括单线性疲劳累计损伤理论、双线性疲劳累计损伤理论、非线性疲劳累计损伤理论等[10]。纵观这些方法，其核心都是考虑应力幅值与循环次数的关系对疲劳寿命的影响，忽略了载荷频率对于材料以及部件疲劳寿命的影响。基于此，国内外相关学者开始研究载荷频率的重要作用，并且通过一系列试验证实了加载频率对疲劳寿命有不可忽视的影响。GUENNEC等[11]研究了在相同的载荷幅值基础上，不同的加载频率对S15C低碳钢疲劳特性的影响。LIN等[12]研究了应力幅值与载荷频率对直齿圆柱齿轮副主动齿轮裂纹萌生寿命与裂纹扩展寿命的影响，并利用台架试验验证两者对疲劳寿命均有影响。

本文研究载荷频率和应力幅值对拖拉机传动系关键零部件的耦合作用，并基于功率密度理论，提出一种疲劳损伤评价与寿命分析方法。首先，对大功率拖拉机变速箱壳体进行典型工况下的有限元分析；然后，基于National Instruments Compact-DAQ系统搭建动态应力测试系统，进行田间作业测试，获取变速箱壳体在犁耕工况下的应力-时间历程；最后，基于实测载荷，利用功率密度法进行疲劳寿命预测，并与基于应力-寿命(S-N)曲线的名义应力法预测结果进行比较，验证基于功率密度法的疲劳寿命分析方法的准确性。

1 仿真分析

1.1 有限元模型建立

采用ANSYS Workbench软件对变速箱壳体进行前处理。首先对变速箱壳体进行预处理，随后对模型进行网格划分。变速箱壳体是一个完整的铸件，材料为QT450-10，弹性模量1.69×105MPa，泊松比0.27，密度7 100 kg/m3。对该壳体使用四面体单元进行网格划分，设置网格最小单元为10 mm，在定义材料时输入属性等参数。划分网格完成后，变速箱壳体中有限元单元数目为118 115个，节点数目为206 756个，网格单元最小雅可比为0.7，如图1所示。

图1 变速箱壳体有限元模型Fig.1 Finite element model of gearbox shell

1.2 静力学分析

大功率拖拉机田间犁耕作业时变速箱壳体所承受的载荷主要包括变速箱齿轮、齿轮轴质量以及自身质量，发动机和后桥等传动系关键零部件带来的附加载荷扭矩，以及犁耕作业时所受外载荷[13-14]。作业时所受动载荷较大，选取动载系数为3[15]。

图2 变速箱壳体静力学分析Fig.2 Static analysis of gearbox shell

根据实际情况以及静力等效原则完成简化加载后，采用ANSYS Workbench的静力学分析模块分析变速箱壳体的受力情况，得到应力分布如图2所示。由图2可知，在静载荷作用下，变速箱壳与发动机连接部分，变速箱壳体与后桥连接部分，变速箱壳体中间隔板轴承孔以及变速箱侧面与底部等部分应力与变形量最大。应力集中区域最容易产生疲劳裂纹，对构件的疲劳寿命影响很大，需着重研究其疲劳损伤情况。

在静力学分析中，最大应力为298.31 MPa，大部分区域应力集中在20～40 MPa，低于许用应力。考虑到静力分析结果、调研情况、实际用户反馈以及应变片粘帖布置方便，选择应力较大的8个点布置应变片，如图3所示。

图3 变速箱壳体测点示意图Fig.3 Measuring points of gear shell

2 试验与分析

2.1 动态应力测试系统组成

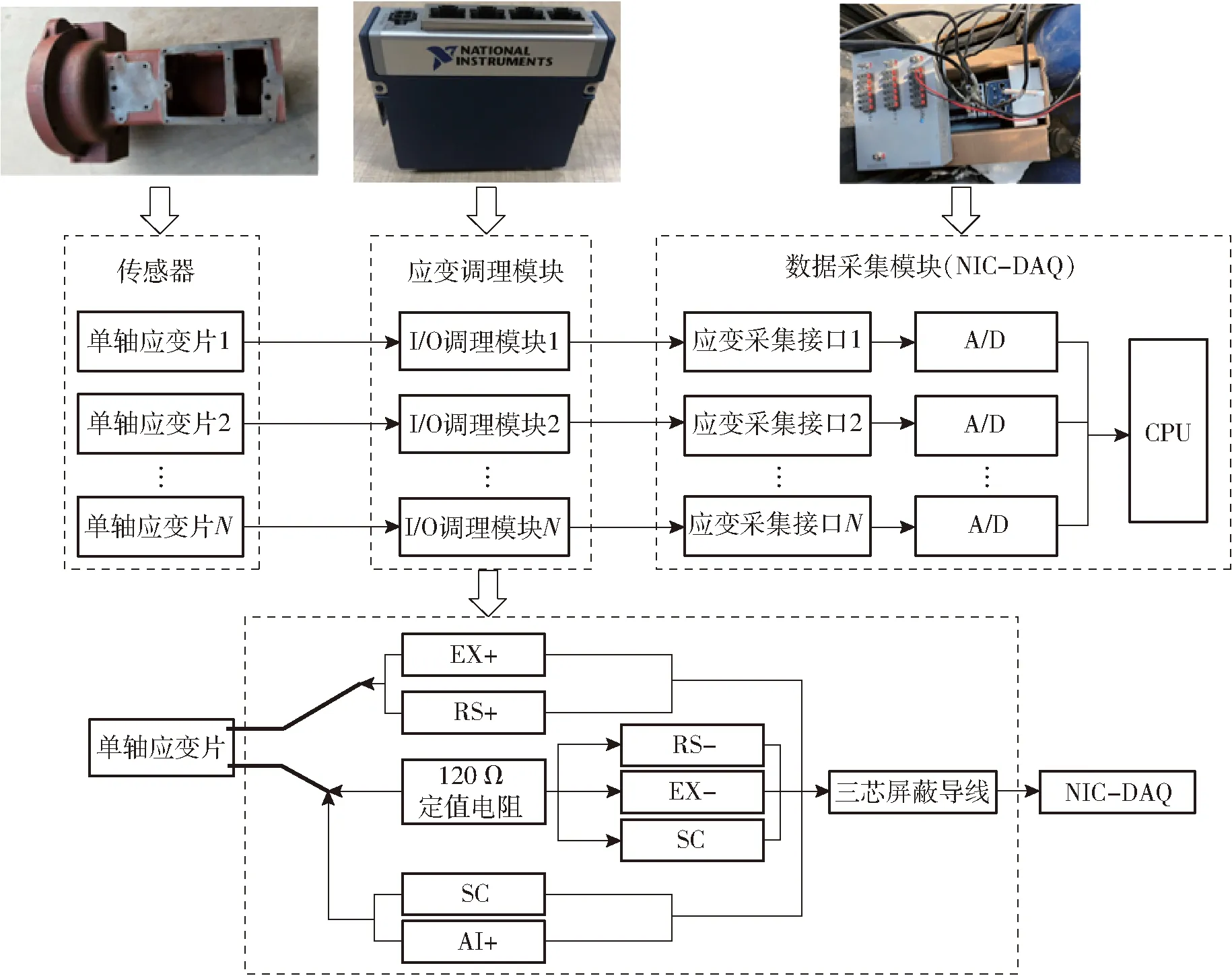
图4 动态应力测试采集系统Fig.4 Dynamic stress test acquisition system

为获取田间作业实测载荷数据以对变速箱壳体进行基于功率密度法的疲劳分析，搭建了以National Instruments Compact-DAQ(NIC-DAQ)系统为主体的样机动态应力测试系统，进行田间犁耕作业等典型工况的应变测试[16]。测试系统主要包括传感器、数据采集模块、数据采集软件，其原理如图4所示。采用NIC-DAQ系统作为数据采集模块， LabVIEW作为程序开发环境进行采集、存储、分析等试验步骤的相关编程。根据奈奎斯特采样定理，为保证频率不混淆，试验设置的采样频率至少需大于分析信号最高频率成分2倍。在工程实际中，采样频率通常至少大于信号中最高频率成分的3～5倍。试验中采样频率为5 000 Hz[17]。8个测点均使用BA120-3AA型单轴高温应变片。部分粘贴效果如图5所示。

2.2 田间作业载荷数据采集

测试地点：北京郊区壤土地块；时间：2018年11月8—12日；温度：12℃。本次样机试验分为道路运输、田间运输、两铧犁耕与五铧犁耕作业4种测试工况。测试作业类型：犁耕，入土深度20 cm，单次作业犁耕数量2铧/5铧，耕作速度4.8 km/h。

2.3 实测数据分析与计算

由于本次试验所选测点的主应力方向均可判断，故使用单轴应变片测量即可。本次试验测得4个典型工况下变速箱壳体8个测点的应变-时间历程，部分测点的信号如图6所示。

图5 应变片粘贴效果Fig.5 Strain gauge paste

图6 部分测点应变-时间历程曲线Fig.6 Strain-time curves at different measuring points

根据胡克定律推算出应力，并进行相应的特征值分析。构件在形变初始阶段应力与应变呈正比，遵循胡克定律[18]。实际应力为

σ=εE

式中σ——应力，MPa

ε——应变

E——弹性模量，MPa

然后分析各个测点在4种工况下的最大应力、最小应力、平均应力、标准差、方差等特征值，分析变速箱壳体实测载荷的可用性，五铧犁耕工况应力如表1所示。并确定试验所取8个测点中的关键点，随后用于疲劳分析和疲劳寿命预测。

本次试验所选工况比较复杂全面，加上作业时整机振动明显，试验测得的载荷数据具有宽频性、幅值时变性以及随机性等特点，因此载荷幅值和加载频率的研究对于变速箱壳体的疲劳分析具有重要意义。

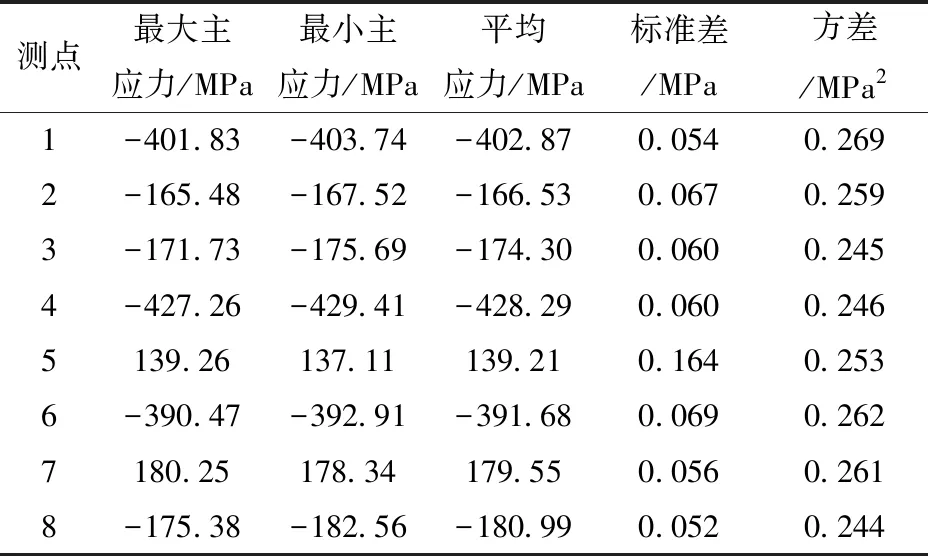
表1 五铧犁耕工况变速箱壳体应力特征值Tab.1 Working condition stress data of gear shell

因为测点4的位置位于传动系关键零部件发动机与变速箱的连接处的下端，不仅受到齿轮以及传动轴的强扭矩，还受到发动机质量引起的附加弯曲载荷。在实际田间作业以及用户反馈中显示测点4所属位置最易产生断裂。在试验结果分析中，显示测点4的应力幅值与均值是各个测点中最大的，并且差异明显，如图7所示。因此，本文后续的研究主要是针对测点4进行相应的基于功率密度的疲劳研究。

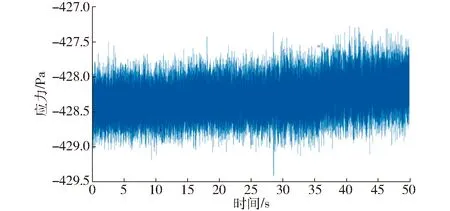
图7 测点4的应力-时间历程曲线Fig.7 Stress-time curve of measuring point 4

3 基于功率密度的疲劳分析方法

3.1 功率密度的基本概念

农业装备工作环境恶劣，工况复杂，工作时主要受到宽频、幅值时变为特点的随机非稳定载荷。对于农业装备疲劳寿命分析不仅要考虑应力幅值与加载次数的关系，还要考虑加载频率、加载顺序等多方面的影响。2008年美国德克萨斯A&M大学的YOONCHAN等[19]在研究高性能封装电子组件时，通过获取共锡焊料的S-N曲线进行一系列可靠性分析，首次提出了应力对时间的梯度，即功率密度的概念。应力对时间梯度dσ/dt在量纲上Pa/s、N/(m2·s)、N·m/(m3·s)、N·m/(s·m3)、W/m3等效。在量纲等效推导过程中可以看出，应力对时间的梯度即是应力载荷在材料单位体积上做功产生的功率，定义为功率密度这一概念。

3.2 短时傅里叶变换

根据傅里叶原理可知，任何试验获取的连续随机信号函数都可分解为无限个∑αisin(2πfit)不同频率和不同振幅的正弦波的叠加。所以，本文中基于该方法使用的实测载荷信号，其功率密度可表示为∑αi2πficos(2πfit)，其中αi和fi分别为载荷幅值和加载频率。利用该方法进行疲劳分析，可以同时反映幅值和频率这两个因素的耦合影响。

采用短时傅里叶变换(STFT)，主要是为了研究实测应力-时间载荷在频域内的相关特征。短时傅里叶变换(STFT)选择特定时间点t=b，首先，使用窗函数h(t)对应力载荷时域函数f(t)加窗，然后，对加窗函数f(t)h(t-b)进行傅里叶变换，来解析应力载荷时域函数f(t)对应的主要特征，即相关频率特性。短时傅里叶变换(STFT)数学表达式为

(1)

式中 STFT(·)——二维频谱函数

h(·)——窗函数

wn——窗口频域宽度

bm——窗口时域宽度

式(1)的离散化形式为

(2)

式中m——时间总步数

n——时间步数

Δt——窗函数宽度

nΔt为每个选定时间点的时刻。

在短时傅里叶变换中，要根据不同的信号类型，尽可能减少能量泄漏以及综合考虑频率分辨率与时间分辨率，选取适合本次分析的窗函数以及相应的参数[20-21]。根据待处理实测载荷的类型，选择汉明窗函数(Hamming window function)，窗口宽度为0.032 s，帧移为0.01 s，其数学表达形式为

(3)

式中h(n,α)——汉明窗函数离散形式，α取0.46

N——窗口宽度

3.3 疲劳分析方法

对于一个给定的材料，假设已知其应力-寿命(S-N)曲线，求应力对时间的梯度以获得该情况下材料的功率密度-寿命曲线方程，即

dS/dt=f1(Nf)

(4)

式中 dS/dt——应力载荷的功率密度函数

Nf——材料发生失效破坏的极限循环总次数

在一定程度的可靠性下

rdS/dt=f1(Nf)

式中r——可靠性系数

求该曲线方程的反函数

Nf=f2(dS/dt)

(5)

对于分析采用的宽频载荷信号，在任意时刻t=t0，dS/dt|t=t0可以利用短时傅里叶变换(STFT)分解成多个与主频Fi和相对应的功率密度Ai=(dS/dt)i相关的余弦信号，即

dS/dt|t=t0=∑Aicos(FiΔt)

(6)

式中Fi——主频率

在特定t=t0时刻的Δt时间内，造成的损伤量表示为

D=∑Ni/Nf，i

(7)

式中D——Δt时间段内的损伤量

Ni——在特定t=t0时刻的Δt时间内主频Fi对应的累积循环次数

Nf，i——材料疲劳失效时主频Fi对应的极限循环次数

在给定的时间步数j内，累积损伤量为

(8)

式中LAD——给定总时间内的累积损伤量

基于功率密度方法，给定的材料失效准则为

(9)

综上所述，基于功率密度的疲劳分析方法技术路线如图8所示。

图8 基于功率密度的疲劳分析方法技术路线图Fig.8 Technology roadmap of fatigue analysis based on power density

4 基于实测载荷的变速箱壳体疲劳分析

4.1 基于功率密度的变速箱壳体疲劳寿命分析

4.1.1变速箱壳体材料的应力-寿命曲线

根据材料疲劳强度相关知识，在典型的S-N曲线图中，AB段表明，在此区域内每一个应力都对应一定的应力循环次数，即相应的疲劳寿命，归纳为疲劳寿命和应力幅值与应力循环次数的关系，即在该应力下对材料造成的累积损伤。BC段表明，只要应力幅值保持在一定的阈值σr以下，即耐久性极限，在这一区域内应力对应的循环次数是无限的，其对应的疲劳寿命也将是无限的，如图9所示。然而，在实际的农业工程中，关键零部件受到高频低振幅的载荷作用，即使应力幅值明显低于耐久性极限，疲劳损伤仍然有较大可能发生。为了解决低频大振幅对于疲劳寿命的影响问题，采用了线性疲劳累计损伤Miner规则的基本形式，在保持AB段斜率的同时将应力-寿命曲线延长到疲劳极限以下，可以有效、定量地描述加载频率对于关键零部件疲劳寿命的影响。

图9 应力-寿命曲线Fig.9 Schematic of S-N curve

本文研究的拖拉机变速箱材料为球墨铸铁QT450-10，抗拉强度σb=450 MPa，屈服强度σs=210 MPa。查找机械设计手册，得材料的疲劳极限循环基数N0=107，循环基数N0对应的疲劳极限σr=0.4σb=180 MPa，等效循环次数Nreq=103，等效循环次数Nreq相对应的等效疲劳极限σreq=0.75σb=337.5 MPa[22]。

将A、B两点坐标代入图9，得到拟合的S-N曲线，并进一步计算得到AB(AC)段方程为

lgS=2.732 75-0.068 25lgNf

(10)

式中S——应力疲劳极限，MPa

将双对数形式的AB段方程转换为单对数AB段方程为

S=(448.7-39.25lgNf)×106

(11)

进一步推导，得到实测载荷时间历程的功率密度-寿命曲线为

(dS/dt)i=Zi(448.7-39.25lgNf，i)×106

(12)

式中Zi——在特定t=t0时刻的功率密度与应力比值的绝对值

故，在可靠性为99.9%时，材料发生疲劳失效的极限循环次数可以用功率密度(dS/dt)表示为

(13)

4.1.2变速箱壳体实测载荷频域特性分析

根据基于功率密度的疲劳寿命分析流程，对图7所示的测点4的应力-时间曲线对时间求导，从而得到测点4的功率密度曲线，如图10所示。

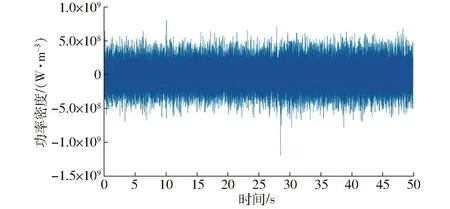
图10 测点4的功率密度-时间曲线Fig.10 Power density-time curve of measuring point 4

由图10可知，t=1.01 s时刻的功率密度，即(dS/dt)t=t0=3.957 1×108W/m3。

对测点4的功率密度曲线进行短时傅里叶变换(STFT)，为了尽可能提取到高频信号，并且同时保证较高的频率分辨率与时间分辨率，对窗函数的窗口宽度选择最优解，以得到最好的分析效果。功率密度曲线的短时傅里叶变换如图11所示。

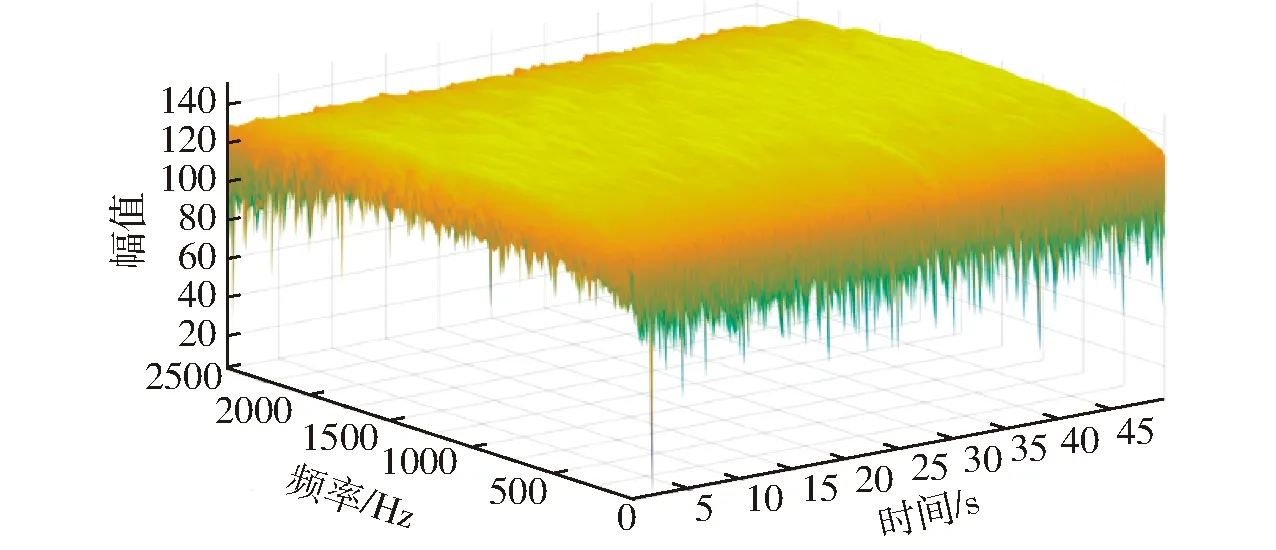
图11 测点4的功率密度-时间曲线的短时傅里叶变换Fig.11 STFT of power density-time curve of measuring point 4

通过对图11相关数值进行归一化处理，可求出任意时刻与相应主频率Fi对应的短时傅里叶变换(STFT)系数。该系数表征某一时刻所有主频与该实测数据频域内最大主频的相对大小关系。短时傅里叶变换(STFT)系数随频率变化的曲线，以t=1.01 s时刻为例，如图12所示。

图12 t=1.01 s时刻的功率密度短时傅里叶变换系数Fig.12 STFT coefficients of power density at time t=1.01 s

由图12可知，在t=1.01 s时，功率密度曲线共包括4个主频率，分别为F1=391 Hz、F2=875 Hz、F3=1 621 Hz、F4=2 168 Hz，与其相对应的短时傅里叶变换(STFT)系数分别为0.891 2、0.969 1、0.930 6、0.908 2。

t=1.01 s时，功率密度可以表示为

dS/dt|t=t0=A(0.891 2cos(391Δt)+

0.969 1cos(875Δt)+0.930 6cos(1 621Δt)+ 0.908 2cos(2 168Δt))

(14)

式中A——t=1.01 s时刻的功率密度幅值

窗函数宽度Δt取0.000 2 s。已知dS/dt|t=t0=3.957 1×108W/m3，根据式(14)可推出A=2.447 8×107W/m3。因此，可分别得到A1=A(0.891 2cos(391Δt))=2.197×107W/m3，A2=A(0.969 1cos(875Δt))=2.37×107W/m3，A3=A(0.930 6cos(1 621Δt))=2.272×107W/m3，A4=A(0.908 2cos(2 168Δt))=2.214×107W/m3。

4.1.3变速箱壳体疲劳寿命分析

在t=1.01 s时，功率密度与应力比值的绝对值Zi=0.757 1，因此，方程(13)简化为

Nf，i=1011.43-3.365×10-8dS/dt|t=t0

(15)

从而可计算出与主频率Fi对应的Δt时间间隔内的累计循环次数Ni和材料疲劳失效的极限循环次数Nf，i。然后，根据式(7)求出主频率Fi在特定t=1.01 s时刻的Δt时间间隔内对变速箱壳体材料的累积损伤量D。最后根据式(8)叠加试验过程中每个时间步数的Δt时间间隔内的累积损伤量LAD，结果如表2所示。

利用基于功率密度的疲劳寿命分析方法，可得出在99.9%可靠性下，大功率拖拉机变速箱壳体危险点测点4位置在50 s田间五铧犁耕试验过程中的累积疲劳损伤量LAD1=5.787×10-7。进而，求出其疲劳寿命为T1=(1/LAD1)×50 s=8.640 3×107s=24 001 h。

表2 t=1.01 s时刻Δt=0.000 2 s时间间隔内变速箱壳体的累积损伤量Tab.2 Accumulated damage at time t=1.01 s during time interval Δt=0.000 2 s

4.2 基于Miner损伤理论的变速箱壳体疲劳寿命预测

Miner理论认为机件在各个应力循环作用下的疲劳损伤是独立进行的，总损伤是各次载荷循环造成的损伤线性累积的结果，忽略了加载频率以及加载顺序对疲劳的影响。当总损伤达到1时，机件发生疲劳失效[23]。

根据Miner损伤理论和名义应力法，当机件承受变幅值载荷时，结构疲劳累积损伤可表示为

(16)

式中Dc——机件的累积损伤量

nj——第j个应力幅值的循环次数

Nj——第j个应力幅值对应S-N曲线上的极限循环次数

使用雨流计数法统计拖拉机变速箱壳体测点4的应力-时间历程，如图13所示。

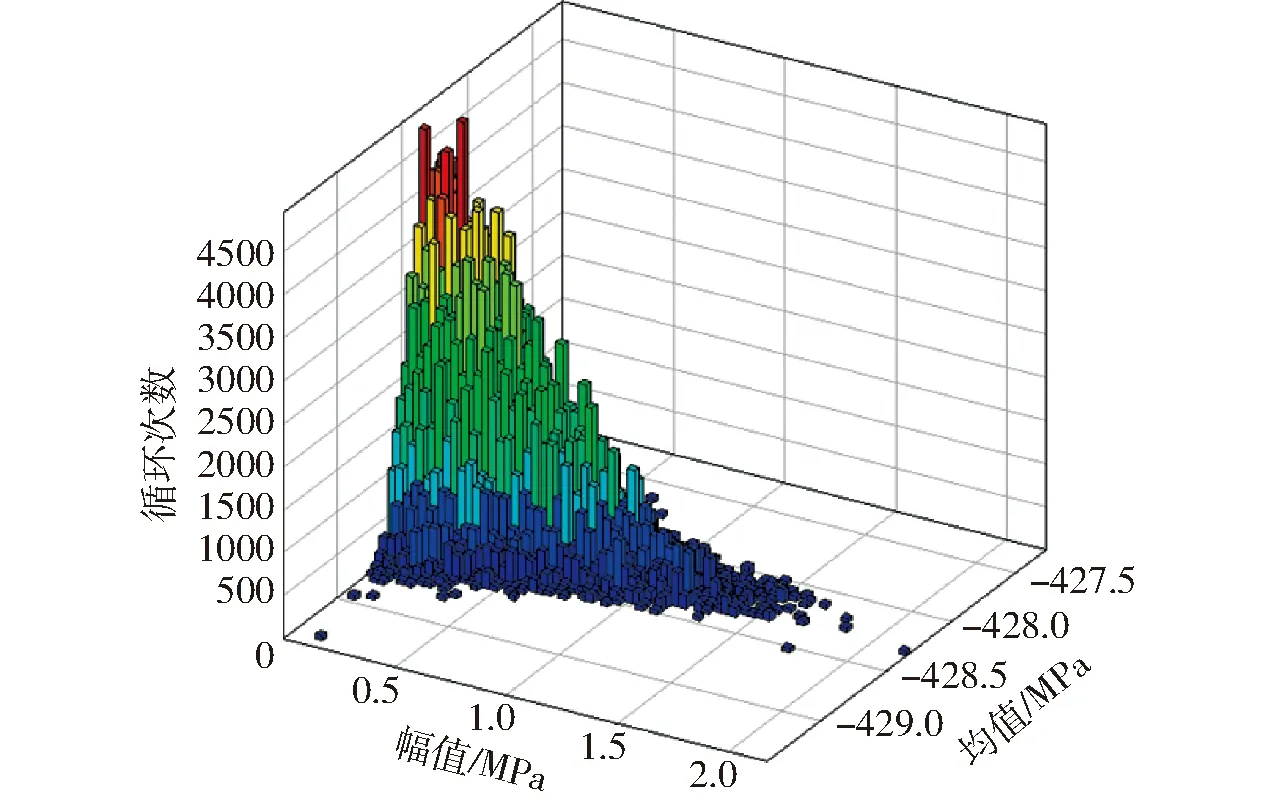
图13 测点4的应力-时间历程计数结果Fig.13 Stress-time history counting results of measuring point 4

结合变速箱壳体的S-N曲线以及式(16)，求得在99.9%可靠性下，测点4在50 s田间五铧犁耕作业过程中疲劳累积损伤量Dc1=3.893×10-7；最后，求得变速箱壳体总疲劳寿命为T2=(1/Dc1)×50 s=1.284×108s=35 676 h。

根据用户反馈和跟踪调查结果显示，该88 kW拖拉机在投入使用后，拖拉机平均每天工作时间为6～8 h，变速箱壳体因为疲劳失效发生故障前的总工作寿命为20 000 h。因此，基于Miner损伤理论和名义应力法的疲劳分析方法由于缺少考虑应力幅值时变、应力频率和加载顺序对寿命的影响，求出的疲劳寿命偏大。本文提出的基于功率密度的疲劳分析方法因为考虑了应力幅值和加载频率对疲劳寿命的耦合作用，求得的结果与实际情况比较吻合。