气动肌肉肘关节MPI迟滞模型与补偿控制
2019-06-27王斌锐靳明涛谢胜龙
王斌锐 芦 韩 靳明涛 谢胜龙
(中国计量大学机电工程学院, 杭州 310018)
0 引言
传统的农业采摘机器人手臂是一个多关节系统,其机械结构和驱动装置具有高质量、高刚度、功率质量比低等特点,但在柔顺性和安全性方面有所欠缺。随着机器人技术的不断发展和完善,新型机器人手臂具有精度高、响应快、承载能力大等特点[1],同时具有良好的柔顺性,以获得更好的安全性和自我恢复能力[2]。
气动肌肉(Pneumatic muscle,PM)作为一种与人体肌肉的生物特性相似的新型驱动器[3],具有结构简单、质量轻、输出力/自重比大、柔性大等优点[4-5],且具有和人体肌肉相似的柔顺性,因而广泛用于医疗辅助康复[6]、仿生[7]和农业机器人[8]等领域。采用气动肌肉作为驱动装置,模仿人体手臂关节结构设计的机械手臂,具有质量轻、柔顺性好、结构简单紧凑、强度大、不易损害操作对象、与人类交互性良好的特点[9]。但由于气动肌肉编织网之间、编织网与橡胶管之间的摩擦、橡胶管的伸缩变形导致的迟滞现象[10],气动肌肉呈现出强非线性,为提高气动肌肉的控制精度,国内外学者进行了大量研究。

图2 不同负载下迟滞曲线Fig.2 Hysteresis curves of different loads
根据迟滞回线的描述方法,迟滞模型可分为微分型迟滞模型和积分型迟滞模型两类[11]。Prandtl-Ishlinskii(PI)模型[12]属于积分型迟滞模型。传统PI(Clas sical Prandtl-Ishlinskii, CPI)模型是由Preisach发展而来,该模型由有限个Play算子或Stop算子加权叠加构成[13],具有结构简单、精度高、便于求逆、能用较少的参数描述迟滞特性曲线,且不存在误差累加等优点,被广泛应用于迟滞非线性系统建模中,但只能用于描述对称的迟滞曲线[14]。LIN等[15]采用依赖于气压的迟滞建模方法推导了气动肌肉的迟滞模型,并与基于广义Bouc_Wen和PI模型的建模方法进行对比,认为PI模型和广义Bouc_Wen模型较Maxwell模型更真实反映了气动肌肉的迟滞特性;SEBASTIAN[16]采用广义Play算子建立了气动肌肉的迟滞模型,并与Maxwell模型、Bouc_Wen模型进行了对比,发现采用广义Play算子对气动肌肉的迟滞拟合效果最优。
对于带有迟滞特性的非线性系统,常用建立逆模型的控制策略,并在系统前面串联逆补偿器来抵消迟滞的影响,即逆模型控制[17]。MINH等[18]采用基于前馈迟滞模型补偿控制的级联控制策略控制单根气动肌肉位置,内、外部回路分别用于控制气动肌肉气压和动力学的非线性,使得气动肌肉对负载的改变具有良好的鲁棒性。由于逆迟滞模型精度依赖于系统的迟滞特性,且对参数敏感,也有学者提出了一些其他控制策略[19]。
本文在CPI模型的基础上,研究改进阈值和包络函数,设计一种可描述非对称迟滞现象的改进PI(Modified Prandtl-Ishlinskii, MPI)模型,采用MPI模型对气动肌肉驱动的肘关节输入气压与输出角之间的非对称迟滞现象进行建模,基于该模型设计前馈积分逆补偿器,搭建积分逆补偿PID控制器,对补偿器的迟滞补偿作用进行验证。
1 气动肌肉肘关节迟滞特性分析
图1中的四连杆肘关节,以气动肌肉为驱动器,可将气动肌肉的线性位移转换为下臂转动。本文对肘关节转动角与气动肌肉内部气压的迟滞特性进行测试。在空载和6、12 kg负载下,对气动肌肉施加变幅值的驱动信号,得到迟滞曲线如图2所示。

图1 肘关节测试平台Fig.1 Elbow joint test platform1.四连杆肘关节 2.SMC比例阀 3.Beckhoff控制器 4.计算机
由图2可知,肘关节转动角与气动肌肉内部气压之间存在迟滞关系,且迟滞环都非对称。随着负载的增加,肘关节迟滞环形状发生变化,肘关节启动位置(即0°位置)附近的迟滞环会逐渐减小。为了更好地控制肘关节,需要建立精确的迟滞模型。
2 肘关节迟滞建模
2.1 CPI模型和MPI模型
CPI模型由不同权值和阈值的Play算子加权叠加构成[20],用来描述系统的迟滞特性,如图3所示。

图3 CPI模型结构Fig.3 Structure of CPI model
基于Play算子的CPI模型可表示为
(1)
式中z(t)——模型输出
p0——系数,需要进行参数辨识得到
v(t)——模型输入
Fri——Play算子输出
ri——第i个算子阈值
p(ri)——CPI模型的权值函数
在改进Play算子[20]的基础上建立MPI模型。改进Play算子的输入与输出关系如图4所示。

图4 改进Play算子的输入输出关系Fig.4 Input and output relationship of modified Play operator
由图4可知,改进Play算子的输出w(t)会沿着曲线γr或γl增加或减少,而不是直线。曲线γr和γl又被称为包络函数。因此改进的Play算子可通过选择合适的包络函数,描述更多种类的迟滞特性曲线。
MPI模型可表示为
(2)
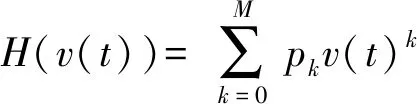
式中H(v(t))——关于输入的多项式函数
pk——多项式系数
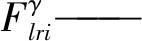
2.2 迟滞建模与参数辨识
对于式(1)CPI模型,权值表达式为
p(ri)=ρe-τri
(3)
对于式(2)MPI模型,包络函数、阈值及多项式表达式为
(4)
ri=αi
(5)
(6)
其中权值表达式同式(3),由式(3)~(6)可知,模型中需辨识的参数有ρ、τ、a0、a1、a2、a3、b0、b1、b2、b3、α、p0、p1等。由于Levenberg-Marquardt方法辨识速度快,且适用于多种场合,故本文基于该方法来进行参数辨识。辨识得到的参数如表1、2所示。

表1 CPI模型参数辨识结果Tab.1 Identification results of CPI model parameters

图5 肘关节迟滞建模结果Fig.5 Hysteresis modeling results of elbow joint
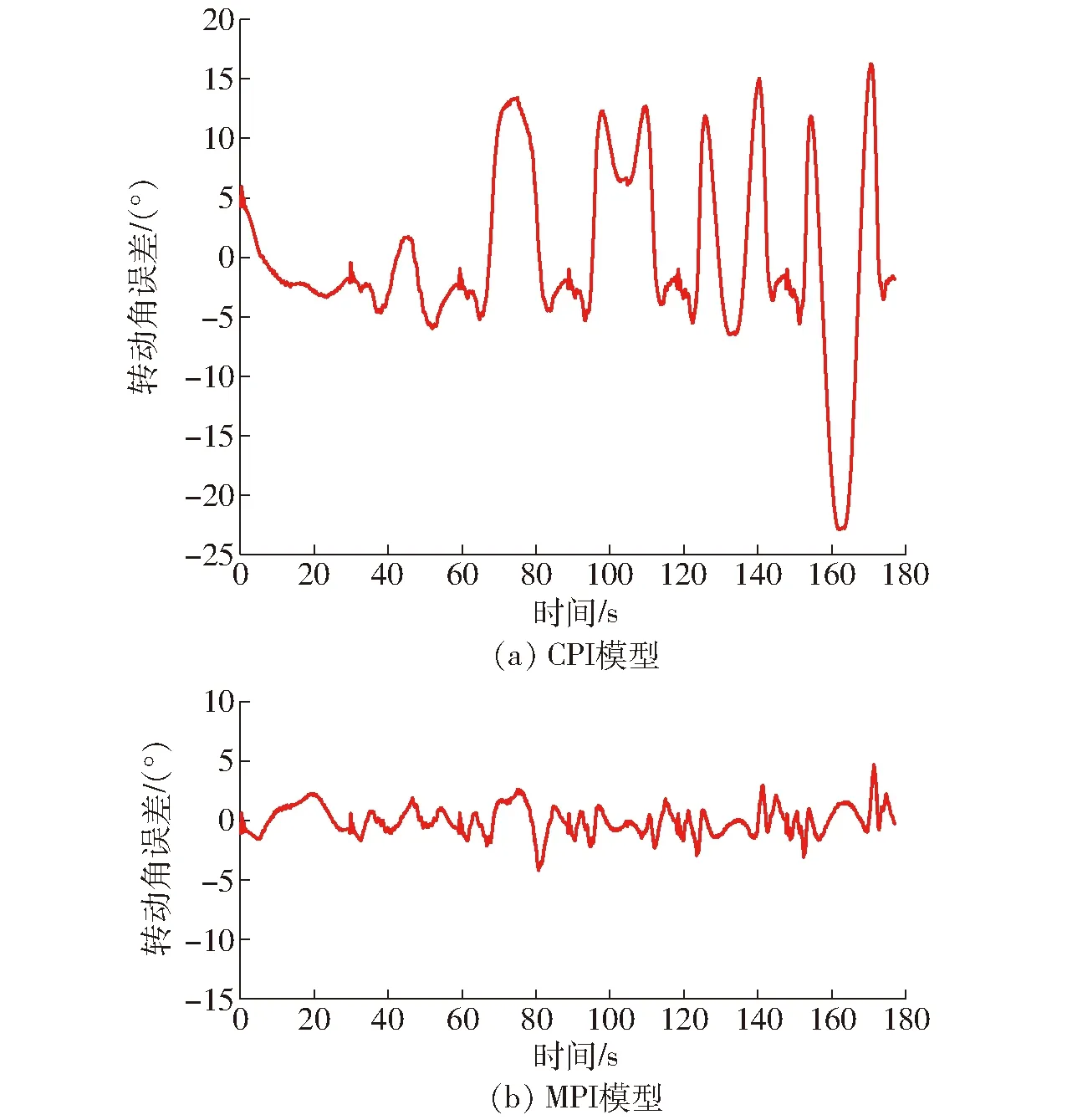
图6 建模误差Fig.6 Modeling error
CPI、MPI模型建模结果如图5、6所示。由图5、6可知,CPI模型只能描述对称的迟滞曲线,MPI模型可以描述非对称迟滞曲线,但在迟滞环的拐点处建模误差较大。采用最大误差与肘关节最大转动角的比值来描述建模准确性,CPI与MPI模型误差率分别为22.67%和4.65%。
3 迟滞补偿控制器设计
基于迟滞模型设计补偿器,综合了PID和逆模型思想的积分逆补偿器(Integral inverse compensator,I-I补偿器),可称为基于MPI模型的积分逆补偿PID控制器(MPI-I-I-PID),包括前馈I-I补偿器和PID控制器。MPI-I-I-PID的控制框图如图7所示。

图7 基于MPI模型的积分逆补偿PID的控制框图Fig.7 Control block diagram of MPI-I-I-PID
设计的控制律可表示为
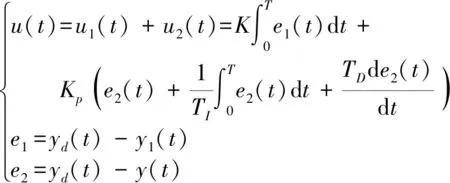
(7)
式中u(t)——控制量u1(t)——补偿量
u2(t)——PID控制器的输出量
K——I-I补偿器的调节参数
e1——理想输入信号与预测信号的差值
Kp——比例系数
e2——理想输入信号与实际输出信号的差值
TI——积分时间常数
TD——微分时间常数
yd(t)——理想输入信号
y1(t)——MPI模型的预测信号
y(t)——实际输出信号
控制量u(t)可映射为气压信号,p1、p2为两侧气动肌肉的初始气压。u(t)映射的气压信号与p1、p2相加减,从而控制肘关节的转动。
4 迟滞补偿控制仿真及实验
4.1 迟滞补偿控制仿真
为验证所设计控制器的有效性,以yd(t)=45sin(πt/25-π/2)+45作为跟踪信号进行了仿真分析,并将仿真结果与PID控制器、基于CPI模型的积分逆补偿PID控制器(CPI-I-I-PID)进行对比,仿真结果与误差如图8所示。
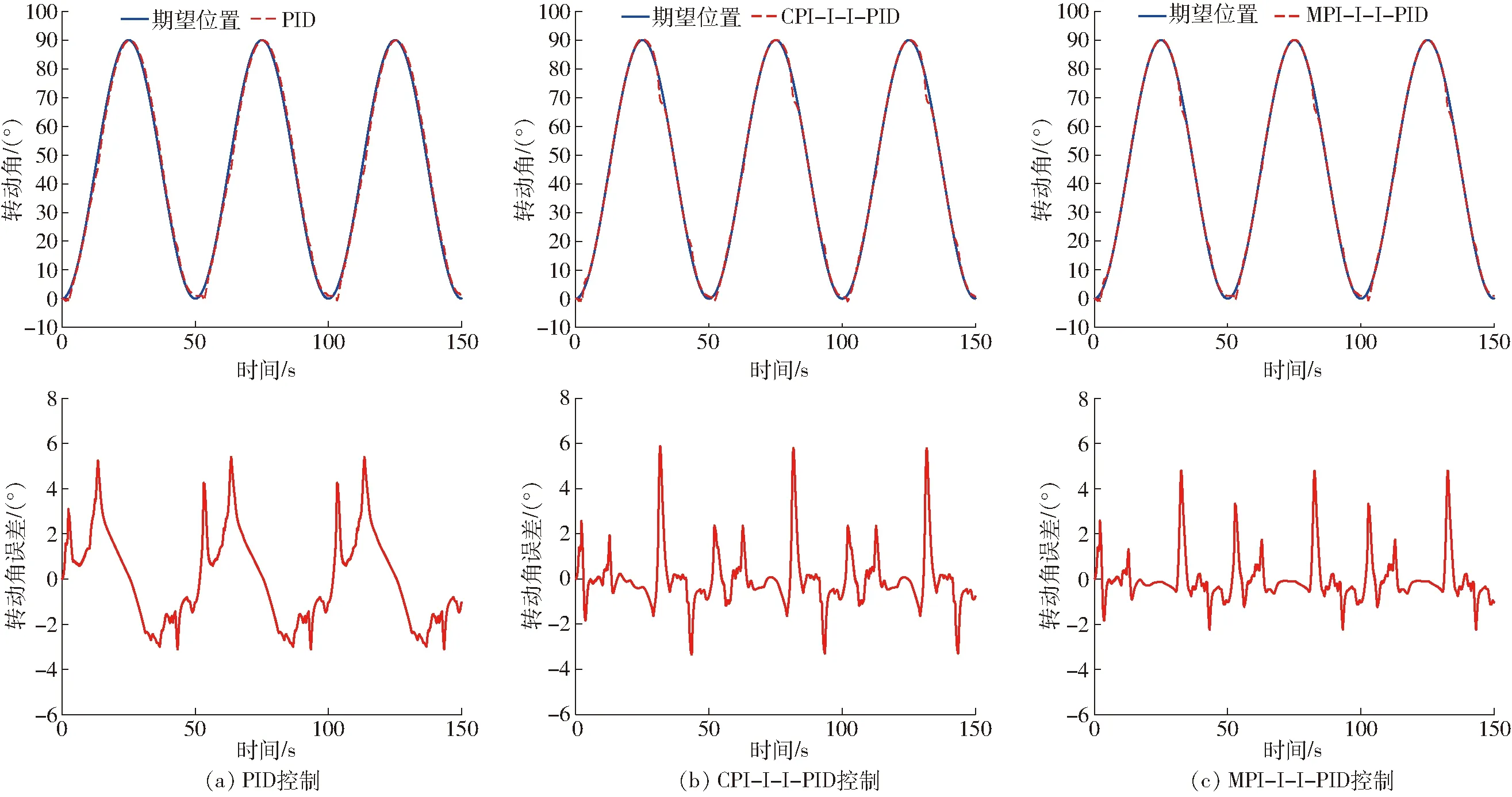
图8 等幅值正弦信号下的仿真结果Fig.8 Simulation results of uniform amplitude sinusoidal signal

图9 不同负载下的正弦跟踪曲线Fig.9 Sinusoidal tracking curves under different loads
由图8可知,MPI-I-I-PID能改善肘关节的迟滞非线性,提高跟踪精度;MPI-I-I-PID的最大跟踪误差小于PID和CPI-I-I-PID;控制仿真的均方根误差分别为1.991 20°、1.401 30°、1.017 10°。所以MPI-I-I-PID控制精度更高。由于MPI模型在迟滞环的拐点处建模误差较大,因此在输入信号的极值处,跟踪误差较大。
4.2 迟滞补偿控制实验
根据PID、CPI-I-I-PID和MPI-I-I-PID控制原理框图,在肘关节实验平台开展实验。给定角度信号为yd(t)=45(sin(πt/25+π/2)+1),周期50 s,幅值90°。在空载和6 kg负载下的控制结果如图9所示,控制误差如图10所示。
由图9对比可见,MPI-I-I-PID控制会使抖动的幅度减小,稳定性提高。由图10可见,MPI-I-I-PID控制会使误差幅值减小。但随着负载的增加,MPI-I-I-PID的控制效果在减弱。
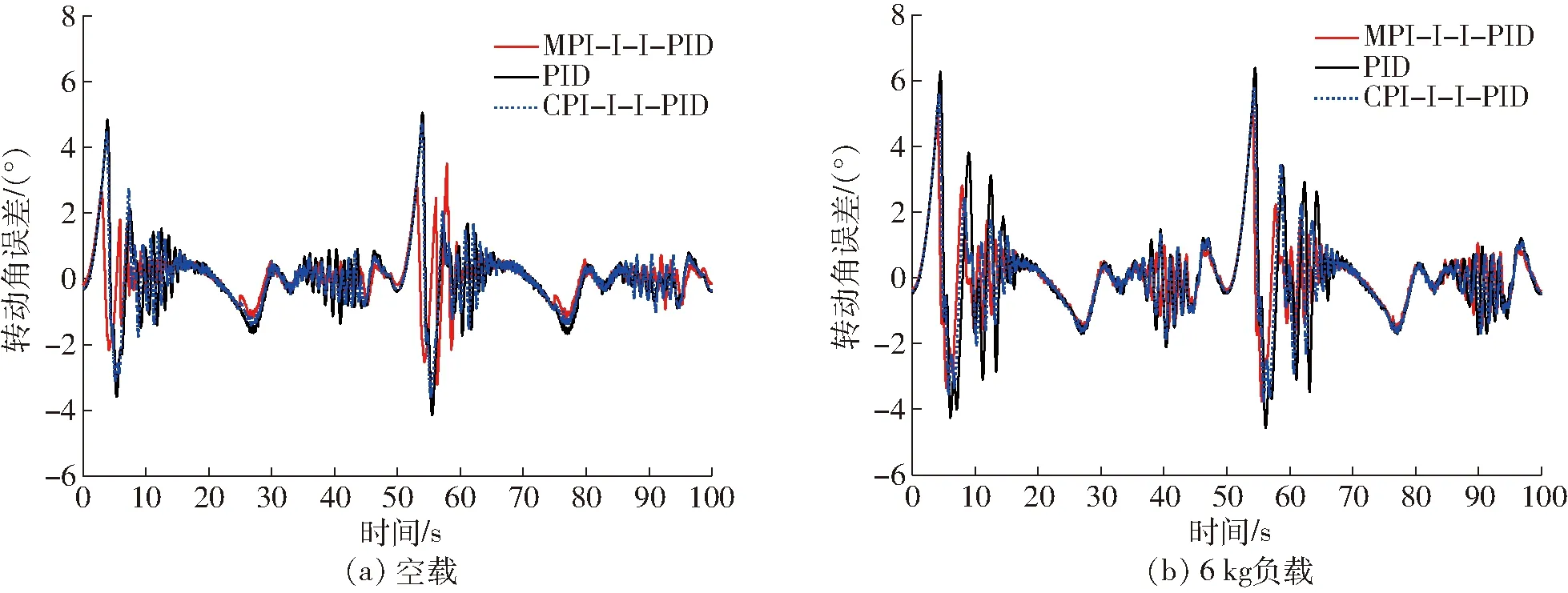
图10 不同负载下跟踪误差曲线Fig.10 Tracking error curves under different loads
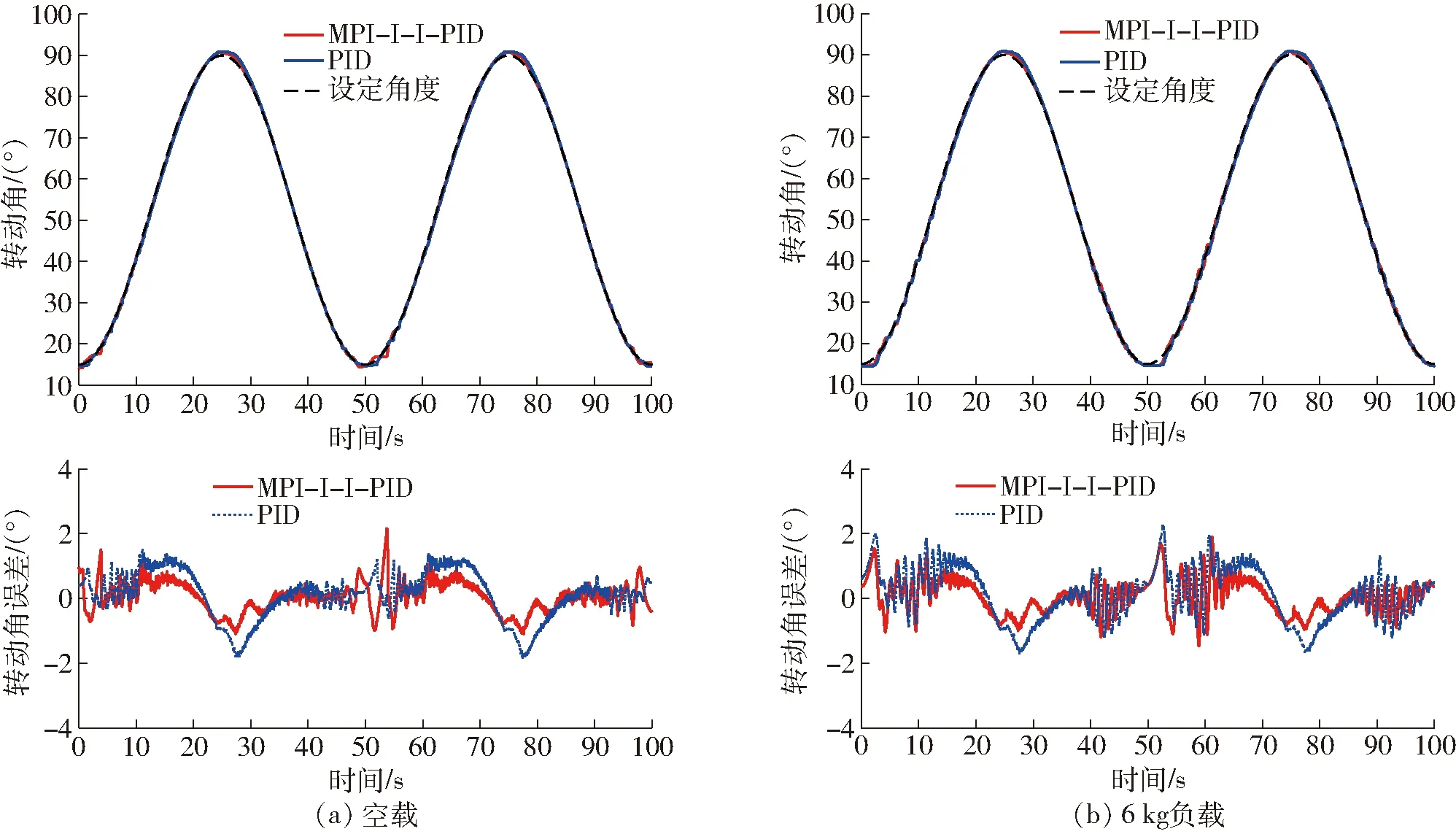
图11 积分逆补偿分段PID正弦跟踪曲线Fig.11 Sinusoidal tracking curves of integral inverse compensation piecewise PID
启动位置附近出现较大误差,原因如下:①气动肌肉在初始充气时,随着气压的增加,并没有收缩,也无输出力,所以存在死区。②由四连杆肘关节机构分析可知,肘关节启动位置时,气动肌肉拉力相对于转轴的力臂较小,传动效率较低。③初始位置需要克服较大静摩擦力,负载越大,静摩擦力越大。
针对上述原因,给定角度信号为:yd(t)=15+37.5(sin(πt/25+π/2)+1),避开机构的死区,在肘关节的0°与90°位置使用分段PID,即采用不同的PID参数。在空载和6 kg负载下的控制跟踪结果如图11所示。
PID、CPI-I-I-PID、MPI-I-I-PID、分段PID(pPID)和分段MPI-I-I-PID(MPI-I-I- pPID)等5种控制转动角均方根误差如表3所示。

表3 不同负载下转动角均方根误差Tab.3 Root mean square error of different loads (°)
由图9~11及表3可知,MPI-I-I-PID控制能减小误差,提高控制精度;但随着负载的增加,积分逆补偿的控制效果在减弱;在底端与顶端使用分段PID并避开肘关节死区的情况下,最大误差明显
减小,与期望轨迹的偏差进一步减小,控制精度进一步提高。
5 结论
(1)MPI模型具有较高的建模精度,能描述肘关节的输入气压与输出角度的迟滞现象。
(2)基于MPI迟滞模型设计的I-I-PID控制器使抖动幅度减小,但随着负载的增加,积分逆补偿控制效果减弱。
(3)在使用分段PID并避开肘关节死区的情况下,肘关节跟踪的最大误差明显减小,受负载影响降低,控制精度提高。
