H+LiH及其同位素替代D+LiD反应的动力学研究

孙鲁艳,庄鑫,刘新国,张庆刚

(山东师范大学物理与电子科学学院，山东 济南 250358 )

在过去的十几年中，人们对LiH2分子体系作了大量的动力学研究，特别是碰撞反应动力学、H的提取和置换及其同位素替代反应，但至今没有对H+LiH基态反应的实验研究。由于LiH及其自由基阳离子LiH+在宇宙化学中所发挥的重要作用，而且该体系电子数少以且动力学性质丰富，使得LiH2体系备受关注[1]。特别是LiH和LiH+的电偶极矩作用比较强，当H+、H和LiH发生碰撞，LiH和LiH+分解或合成时，可以给万有引力坍塌提供能量，这对研究早期宇宙化学具有重要意义[2]。

精确的势能面是研究LiH2分子体系化学反应动力学的前提。到目前为止，H+LiH反应基态势能面中最具代表性是Dunne等[3]构建的半经验势能面(后面简称D-PES)，Roy等[4]分别基于此势能面进行了动力学研究，均没有发现势阱或势垒的存在； Prudente等[5]将D-PES进行了完善(简称P-PES)，且发现最小反应路径上不存在势垒，而Liu等[6]和Sha等[7]基于此势能面作动力学分析时，却发现在直线构型存在小势垒；Wernli等[8]采用多参考组态方法构建的势能面(简称W-PES),与D-PES和P-PES相比，采用的计算方法和拟合方法更加精确。Roy等[4,7]认为W-PES没有势垒或势阱的存在。此外，2015年Yuan等[9]构建了该体系基态更为精确的势能面(Yuan-PES)，其光谱常数较P-PES和W-PES更准确，但其动力学结果与Wernli等[8]的结果相一致，即不存在势垒或势阱。基于此势能面，HE等[10]利用含时波包和准经典轨线方法对该体系不同同位素替代反应进行了动力学研究，发现D+LiH的积分截面最大，H+LiH的速率常数最大，且该势能面没有势垒的存在。

为进一步明确该体系有关反应通道上垒和阱是否存在的争论和不确定性,更加详细地探究LiH2分子体系丰富的动力学性质，本研究组前期基于多参考组态相互作用方法计算了大量从头算能量点，并用基组外推模型将其外推至完备基组，构建出高精度全维基态势能面(Li-PES)[11]。该势能面较P-PES和W-PES二体项解离能和平衡键长更接近实验值，拟合误差也更小，因此我们构建的势能面较P-PES和W-PES的精确度更高。基于此势能面，前期进行了包括振动激发、转动激发在低碰撞能下对该体系动力学影响的理论研究，但是尚未有基于该势能面对H+LiH、D+LiD动力学性质的研究。为丰富该体系基于新势能面的相关动力学性质，本文在Yuan-PES和Li-PES两个势能面上开展了H+LiH及其同位素替代D+LiD反应的动力学理论研究与计算。

1 理论方法

准经典轨线[12-13]是在经典力学基础上发展的散射理论，考虑了量子力学效应的影响。根据波恩-奥本海默近似，在LiH2体系势能面的基础上求解原子核运动的哈密顿方程。准经典轨线方法就是模拟反应空间，选择符合条件的轨线来研究动力学性质。完整的反应动力学研究包括两个方面：标量性质和矢量性质，反应的标量性质包括积分反应截面和反应几率等，矢量性质包括反应物和产物的相对速度方向与角动量取向以及这些矢量间的相互关系。

1.1 定向和取向

定向和取向[14]是用来描述反应中角动量各向异性的两个量，角动量的定向分布指角动量的方向指向某一特定方向，取向分布指角动量平行或垂直于某一特定方向。

1.2 产物转动角动量分布

在研究产物转动角动量j′时选Z轴为参考轴。当产物的角动量j′关于Z轴对称分布时，其描述矢量方向的函数可以用Legendre多项式展开[15]：

(3)

我们只计算当l=2时的二阶角动量分布情况：

(4)

其中，θ为转动角动量j′与Z轴的夹角。

1.3 k-k′-j′矢量相关的准经典描述

在质心坐标系中，反应物相对速度k,产物相对速度k′，产物转动角动量j′3个矢量的全三维分布可以用极化微分反应截面来展开[15]：

,

(5)

其中，积分反应截面可以用以下公式计算

(6)

k-k′-j′三矢量相关的极角分布用傅里叶级数展开为：

(7)

本文采用准经典轨线方法分别在Li-PES和Yuan-PES势能面上对LiH2体系进行了反应动力学计算研究。首先，进行了振转基态下的准经典轨线计算，初始状态H/D原子到LiH/D质心的距离设定为20 Å，此时它们之间的相互作用可以忽略不计。积分步长设定为0.1 fs，足够小的积分步长确保了计算的准确性。初始振转量子数设为0(v=0，j=0)，碰撞能取0至30 kcal/mol，间隔1 kcal/mol，共31个碰撞能，每一碰撞能下选择100 000条轨线来模拟动力学。然后分别计算研究了振动激发(υ=0,1,2,3，j=0)和转动激发(υ=0，j=10,20,30)对该体系两个反应的动力学影响。

2 结果与讨论

在0～30 kcal/mol的能量范围内进行了准经典轨线计算，为比较Li-PES和Yuan-PES的差异，对两个势能面H+LiH、D+LiD进行了动力学研究，包括标量性质和矢量相关性质的研究。

2.1 碰撞能和振转激发对积分反应截面的影响

分别基于Li-PES和Yuan-PES,用准经典轨线方法选取了碰撞能分别为0、5、10、20、30 kcal/mol的H+LiH、D+LiD反应的反应几率和积分反应截面。结果显示，积分反应截面与最大碰撞参数bmax和反应几率Pr有关(见表1)。且碰撞能对积分反应截面的影响较明显,碰撞能较高时，基于Yuan-PES计算的最大碰撞参数和反应几率较基于Li-PES小，Yuan-PES的积分反应截面小于Li-PES的积分反应截面，Li-PES的积分反应截面与Liu等[6]的理论值更接近；碰撞能较低时反之。

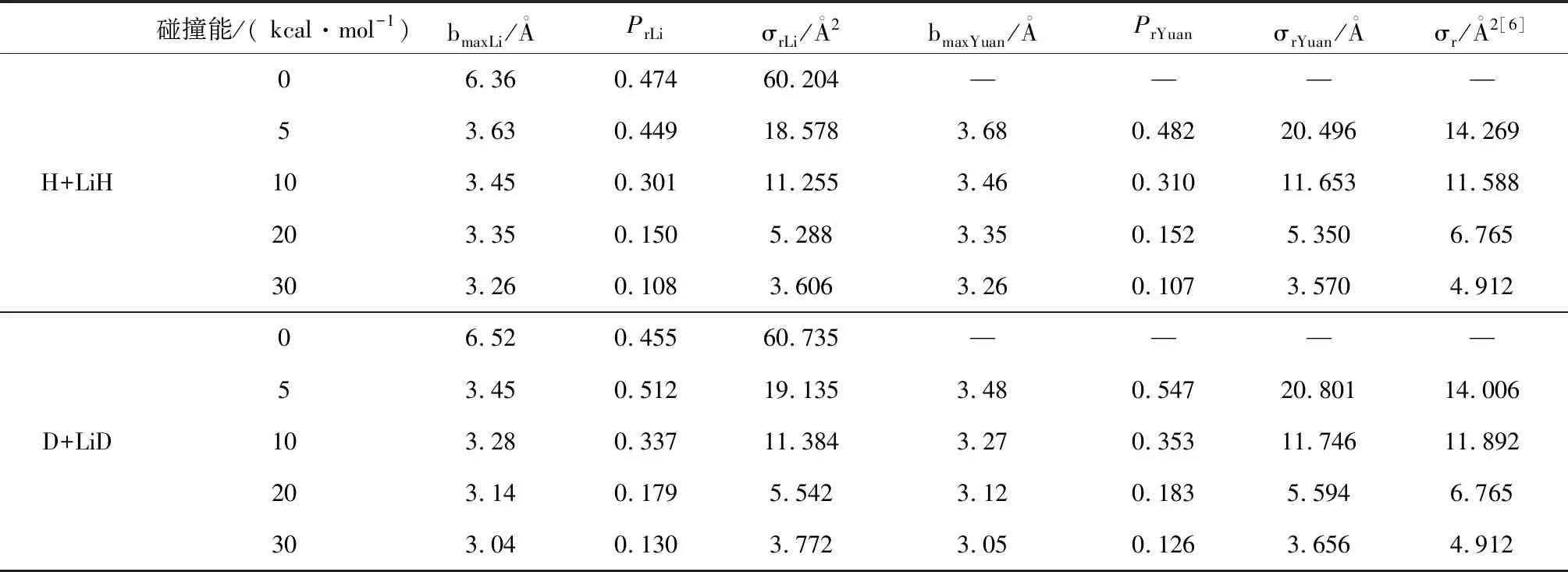
表1不同碰撞能下H+LiH、D+LiD的反应几率和积分反应截面及其与其他理论值的比较

当碰撞能等于5 kcal/mol时，Li-PES和Yuan-PES的积分反应截面明显高于Liu等[6]的理论数值，对于这一现象的解释，可以从势能面的基本特征考虑， 动力学分析是基于P-PES势能面，并且证明了该面存在一个0.092 8 eV的垒，而Li-PES是不存在阱或垒的，但对Yuan-PES进行准经典轨线计算时，发现其需至少0.11 kcal/mol的能量才能正常运行，说明在此势能面的最小反应路径上，该反应的阈值为0.11 kcal/mol，即存在0.11 kcal/mol的小垒。势能面的差异导致动力学性质有所不同，碰撞能较低时尤为明显。

图1给出了利用准经典轨线方法在Li-PES和Yuan-PES上计算的H+LiH反应的积分反应截面与Roy等[4]、Liu等[6]以及Sha等[7]计算的积分反应截面的比较结果。从图1中可以看出，积分反应截面随着碰撞能的增加而减小。Roy等[4]的含时波包和Sha等[7]的准经典轨线值结果都是基于W-PES进行动力学计算得到的。由图1可知，基于同一个势能面而不同的方法计算得到的积分反应截面结果不同，量子方法的积分反应截面较准经典方法的要高。Sha-P-PES、Liu-PES的准经典轨线结果是基于P-PES势能面得到的，当碰撞能较高时，积分反应截面相吻合，而碰撞能较低时，Sha-P-PES的积分反应截面较Liu-PES高。我们运用准经典轨线方法，基于Li-PES和Yuan-PES两个不同的势能面计算得到了积分反应截面。整体走势与其他理论值是一致的，但在碰撞能较高时，Li-PES的积分反应截面较Yuan-PES略高，且与其他理论值相比较低；而碰撞能较低时，Yuan-PES的积分反应截面较Li-PES的高，且基于W-PES计算的积分反应截面最大碰撞能大于5 kcal/mol时，垒的存在对积分反应截面的影响较小。

图1 H+LiH反应的积分反应截面及与其他理论值的比较Fig.1 Comparison of integral cross sections of H+LiH reaction with other theoretical values

图2给出了不同振动态对积分反应截面的影响，并与Roy等[4]的理论值做了比较。随着振动量子数的增加，积分反应截面减小。并且碰撞能越高，随着振动量子数的增加，积分反应截面的变化量越小。说明在低碰撞能下,振动激发对积分反应截面的影响较大。在碰撞能较低时，Yuan-PES的积分反应截面略高于Li-PES;而碰撞能较高时，Li-PES的积分反应截面在振动量子数υ=0,1时较Chen略高，而在υ=2,3时较Yuan-PES略低，两个势能面的差异在低碰撞能时体现得更明显。与Roy等[4]人的积分反应截面相比，结果偏小，但整体趋势是一致的，这是采用不同的面和不同的动力学分析方法导致的。

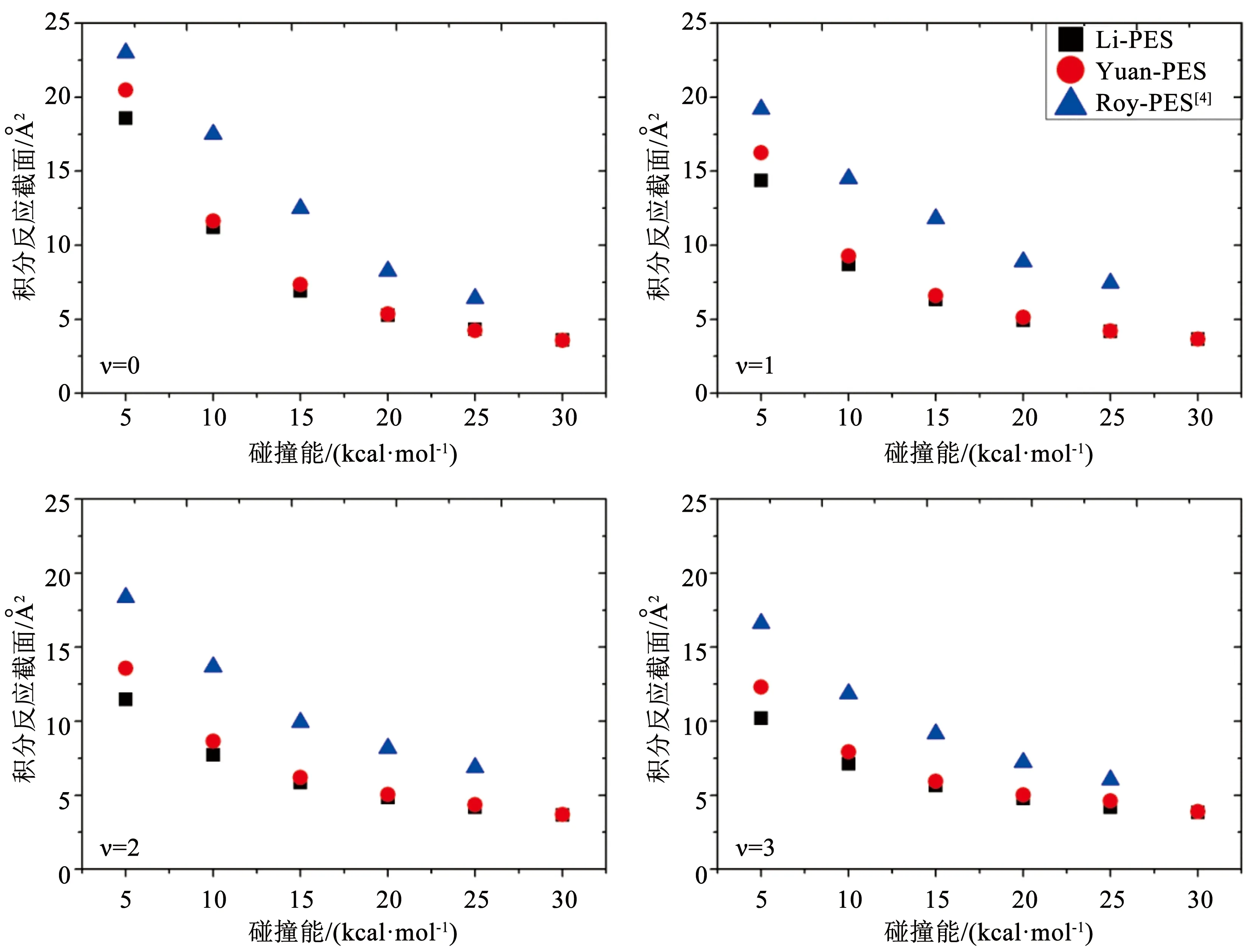
图2 不同振动激发下H+LiH反应的积分反应截面及与其他理论值的比较Fig.2 Comparison of integral cross sections of H+LiH reaction at different vibration excitations with other theoretical values

图3给出了不同转动激发态下Li-PES、Yuan-PES的H+LiH、D+LiD反应的积分反应截面。在低碰撞能下，积分反应截面随碰撞能的增加迅速降低；在较高碰撞能下，积分反应截面随碰撞能的变化很缓慢，这是由于该反应是放热反应且无垒或存在很小的垒造成的。不同的转动量子数其积分反应截面也不同，这归因于H/D+LiH/D反应是纯粹的放热反应。当处于同一转动态时，低碰撞能下的H+LiH反应的积分反应截面低于D+LiD反应的积分反应截面，而对于高碰撞能下时，两个反应的积分反应截面相差很小。这说明碰撞能较低时，转动态对其影响较大。并且， Li-PES的积分反应截面较Yuan-PES略低，低碰撞能下更明显，从势能面的主要特征考虑，说明低碰撞能时早期小势垒对该反应有促进作用。当质量数增大时，两个势能面的积分反应截面减小。由于质量数不同，积分反应截面的差距随着转动量子数的增加而增大。

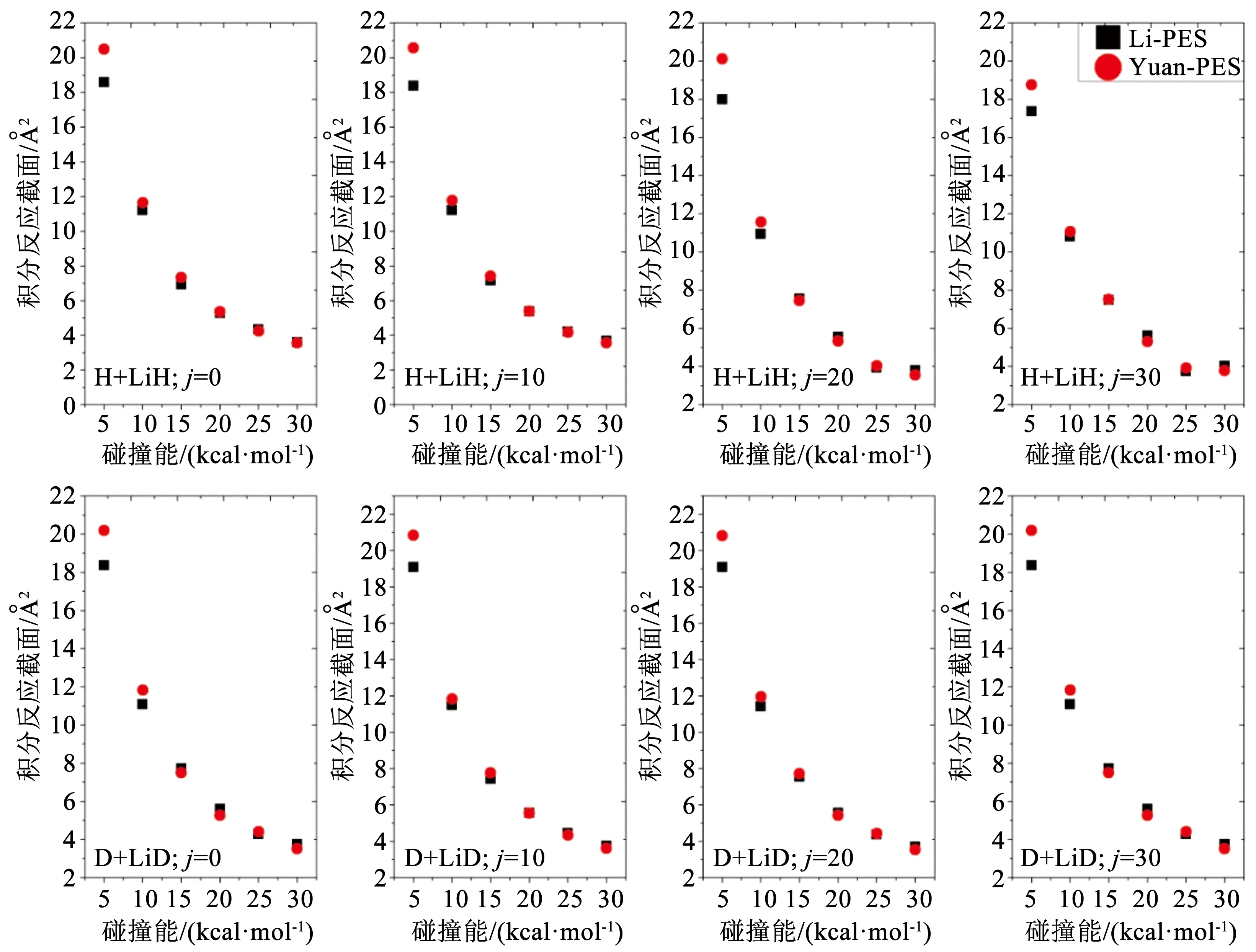
图3 转动激发下H+LiH、D+LiD反应的积分反应截面Fig.3 Integral cross sections of H+LiH and D+LiD reactions at different rotational excitation

2.2 振动态对H+HLi→H2+Li反应P(Ør)函数影响

图4给出的是碰撞能为 20 kcal/mol时，不同振动态下Li-PES和Yuan-PES两个势能面的P(Ør)函数关系。反应物速度k和产物速度k′组成的平面我们称为散射平面，由图4可见，在所有碰撞能下，2个势能面的P(Ør)函数图像是不对称分布的，图像存在一高一低2个峰值，这说明产物存在特别明显的定向特征，这是由于原子与分子在不断的接近过程中，会随着距离的越来越近，分子间作用势表现为斥力作用，从而产生定向效应。而两个峰值都出现在y轴上，且Ør=90°时的峰值高于Ør=270°时的峰值，这说明产物角动量是定向于y轴正方向的。当振动量子数从υ=0增加到υ=1时，Yuan-PES在Ør=90°时所对应的峰值减小，而Li-PES在此时所对应的峰值增大，说明振动量子数从υ=0到υ=1的过程中，Yuan-PES所对应的产物转动角动量的取向特征减弱，而Li-PES所对应的产物分子的转动角动量的取向特征增强；Ør=270°时，Yuan-PES和Li-PES所对应的峰值都增大，但Yuan-PES在此刻对应的是中间低两侧高且尖锐的峰，呈现V型劈裂状，而Li-PES对应的是比较圆润的峰，这说明Yuan-PES的产物有在散射平面外转动的倾向，而Li-PES的产物倾向于在散射平面内转动，由平面内机理控制。当振动量子数从υ=1增加到υ=2时，Yuan-PES在Ør=90°时所对应的峰值增大，而Li-PES在此时所对应的峰值减小，说明振动量子数从υ=1到υ=2的过程中，Yuan-PES所对应的产物转动角动量的取向特征增强，而Li-PES所对应的产物分子的转动角动量的取向特征减弱；Ør=270°时，Yuan-PES和Li-PES所对应的峰值都增大，但Li-PES在此刻对应的图像由较为圆润的峰变成中间低两侧高且尖锐呈现V型劈裂状的峰，而Yuan-PES则是由V型劈裂状的两个尖锐的峰变成一个比较圆润的峰，这说明Yuan-PES的产物由在散射平面外转动转变成在散射平面内转动的倾向，而Li-PES的产物则是由倾向于在散射平面内转动变成倾向于在散射平面外转动，当υ=1到υ=2的变化过程中，Yuan-PES的产物角动量的转动情况由平面外机理控制转变为由平面内机理控制，而Li-PES的产物角动量的转动情况则是由平面内机理控制转变为平面外机理控制。当振动量子数υ从2增加到3时，Yuan-PES在Ør=90°时所对应的峰值增大，而Li-PES在此时所对应的峰值明显减小，说明振动量子数从υ=2到υ=3的过程中，Yuan-PES所对应的产物转动角动量的取向特征增强，而Li-PES所对应的产物分子的转动角动量的取向特征明显减弱；Ør=270°时，Yuan-PES和Li-PES所对应的峰值都增大，尤其是Yuan-PES的峰值是明显增大的，而Li-PES则是由V型劈裂状的两个尖锐的峰变成一个比较圆润的峰，这说明Yuan-PES的产物转动角动量有在散射平面内转动的倾向，而Li-PES的产物则是由倾向于在散射平面外转动变成倾向于在散射平面内转动，当υ=1到υ=2的变化过程中，Yuan-PES的产物角动量的转动情况由平面内机理控制，而Li-PES的产物角动量的转动情况则是由平面外机理控制转变为平面内机理控制。

图4 振动态对H+HLi→H2+Li反应P(Ør)函数影响Fig. 4 Effects of vibrational excitation on function of P(Ør) of H+HLi→H2+Li

2.3 同位素替代对极化微分反应截面的影响

图5给出了碰撞能为20 kcal/mol H+LiH、D+LiD反应的极化微分反应截面函数(2π/σ)(dσ00/dωt)。从图5中发现LiH2体系的放热提取反应具有很明显的前向散射特点，且Yuan-PES的前向散射程度较Li-PES强。除此之外，还可以得出以下结论：当发生同位素替代时，H+LiH向前散射的趋势比D+LiD的趋势要明显。

图5 H+LiH和D+LiD的极化微分反应截面Fig.5 Polarization differential reaction cross sections of H+LiH and D+LiD

3 结论

本文基于两个LiHH体系基态势能面Li-PES和Yuan-PES，运用准经典轨线方法研究了在0～30 kcal/mol能量范围内，碰撞能、同位素效应、振动激发对H+LiH反应动力学性质的影响。讨论了Li-PES和Yuan-PES在基态下不同碰撞能对最大碰撞参数、反应几率和积分反应截面的影响，积分反应截面随着碰撞能的增大明显减小，且Li-PES的积分反应截面较Yuan-PES更接近Dunne等[3]的理论值。反应几率和积分反应截面随碰撞能的增大而减小，低碰撞能对该反应具有促进作用，碰撞能较低时Yuan-PES的反应几率和积分反应截面大于Li-PES，碰撞能较高时反之,并且发现Yuan-PES存在小势垒。H+LiH反应的积分反应截面较众理论值较低。Li-PES的积分反应截面在振动量子数υ=0,1时较Chen-PES略高，而在υ=2,3时较Yuan-PES略低，而两个势能面的差异在低碰撞能时体现得更明显。在研究转动量子数对其影响时，发现当质量数增大时，两个势能面的积分反应截面减小，且随着转动量子数的增加，由于质量数不同导致的积分反应截面的差距增大。振动量子数对两个势能面的产物角动量在散射平面内的转动机理控制也是不同的。

Yuan-PES的前向散射程度较Li-PES强，H+LiH向前散射的趋势比D+LiD的趋势要明显。