基于MPC下车辆自主避障算法*

2019-06-25胡均平曾武杨李勇成

传感器与微系统 2019年7期

胡均平, 曾武杨, 李勇成

(中南大学机电工程学院,湖南长沙 410083)

0 引言

近些年来,交通安全问题日趋严重,提高车辆行驶安全系统已经成了各大汽车厂商亟待解决的问题。在车辆的安全行驶过程中,主动避障系统起着十分重要的作用。智能车辆的避障车辆的纵向制动性能,如在湿滑路面车辆通过制动达到避障效果,湿路上的制动距离受车辆重量和速度的显着影响[1,2]。车辆在干沥青路面以70～80 kg/h行驶,车辆转向避障距离总是小于制动避障距离[3]。但驾驶员发现制动避障距离不足时,就会开始选择转向避障[4,5]。转向避障策略现己有许多种控制方式,避障思路主要可以分为3个步骤：障碍识别、障碍分析和车辆避障。现如今控制法的研究相对成熟。如模糊逻辑法、神经网络法[6]、占据栅格法[7]、空间搜索法[8]、势场法[9]等。Falcone P等人通过采用模型预测控制(model predictive control,MPC)策略,通过将车辆状态限制为轮胎力生成的线性状态来跟踪光滑路上的车辆避障轨迹[10,11]。Katriniok J等人类似地追踪了车道变化轨迹,但是扩展了稳定性标准以结合非线性车辆动力学,增加了控制动作以追踪轨迹[12]。文献[13,14]提出了层次框架,高层次的MPC算法于障碍避免轨迹与低层MPC算法于轨迹跟踪相结合。综上所述,传统的避障方法虽然理论完善,但是存在着潜在的问题。即稳定性约束与车辆避障行为可能存在冲突,因此,稳定性约束影响避障轨迹规划,从而导致车辆避障失败发生碰撞。

本文为了避免这种现象,将轨迹生成和轨迹跟踪集成在一个控制系统中,将避免障碍物约束添加到MPC控制器,允许控制器修改输入数据从而达到避障效果。

1 车辆模型设计

智能车辆避障路径规划系统主要是完成障碍物识别、避障路径规划、保障车辆沿规划的路径行驶等三方面的任务。在本文中,假设障碍物识别的问题已经解决,即避障路径规划前已经获知车辆行驶方向上障碍物的具体位置信息及障碍物影响范围。在获知障碍物信息的基础上,注重于避障路径的规划和保障智能车辆按照指定路径行驶的稳定性等技术难题。

1.1 动力学模型

本文只考虑路面对轮胎的摩擦力以及路面对轮胎的垂直作用力,空气动力学对车辆运动的影响在此不予考量。将车身视作刚体,且质量分布均匀,假设车辆在给定的纵向速度Ux下行驶。建立2自由度车辆运动模型,考虑了横向速度Uy和偏航速率r。整车运动分析图如图1所示[15～17]。

图1 车辆模型坐标系

由图1所示可得车辆运动方程

(1)

式中Fyf和Fyr分别为前轮胎和后轮胎的侧向力,m为整车质量,Izz为车辆绕z轴的惯性矩,a和b分别是车辆质心到前后轮轴的距离。

本文采用Pacejka2002轮胎模型计算前轮轮胎力Fyf和后轮轮胎力Fyr。轮胎横向力计算方程为

(2)

由于前轮转向角δ与Fyf相关,因此,通过Fyf可求得δ

(3)

对其进行模型预测控制,设线性模型为

x′=Ax+BFyf+CFyr+D

(4)

式中x=[UyrΔΨse],通过式(1)、式(2)可知

通过对线性模型离散化,采用时间间隔为Ts,可得离散系统线性模型

x(k+1)=Adx(k)+BdFyf(k)+CdFyr(k)+Dd

(5)

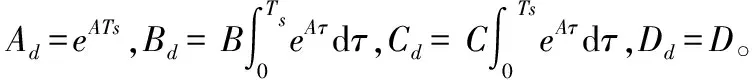
1.2 稳定性约束

车辆稳定和避免碰撞的目标是根据状态空间中的区域定义车辆状态情况,如图2所示。该控制器使用Beal和Gerdes状态空间函数,通过轮胎所产生最大的轮胎力来限制车辆的速度Uy和r。车辆最大横向速度Uy,max和r为

Uy,max=Uxαr+br

(6)

(7)

式中a和b分别为从车辆重心到前轴和后轴的距离。

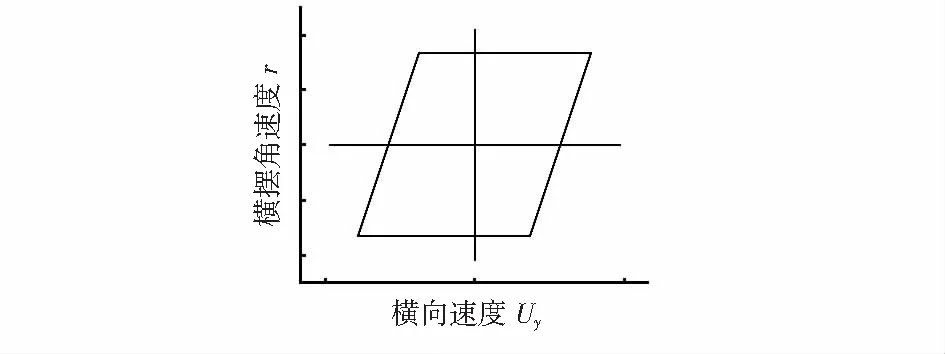
图2 横摆角速度和横向速度约束

考虑车辆稳定性时的另一个重要限制是后轮胎的饱和度。根据侧滑角αr求得轮胎力大小

(8)

最大质心侧偏角

(9)

横向偏移界限emax和emin作为沿着避开障碍物并留在道路上的路径的距离s的函数。对车辆的侧向偏移采用下述约束

(10)

2 控制器系统设计

通过轨迹及稳定性约束定义了控制器必须控制的目标。MPC控制器根据简易化的纵向控制器输入一组纵向数据,然后将横向输入数据进行优化处理,最后将其输入车辆信息中。同时车辆状态不断反馈其控制器,其整体控制结构如图3所示。

图3 控制器系统设计原理

2.1 纵向控制器

纵向控制器是根据在预测范围内所测量得纵向速度来确定纵向力。本文假设车辆的纵向动力学看作质点。在MPC预测范围内的每个点k处,使用以下反馈控制方案

(11)

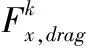
2.2 横向控制器

基于离散系统线性模型对其进行MPC优化从而得到轮胎力,因此,车辆后轮胎滑移角度的置信区域为

(12)

将稳定性约束表示为

(13)

将横向误差表示为

(14)

对车辆避障方案进行加权优化得

(15)

2.3 车辆状态及输出预测

假设车辆的预测范围为p,控制范围为m,则m≤p。对于超出控制范围的采样m,假设控制输入保持不变,即u(k+m)=u(k+m+1)=…=u(k+p-1)。根据离散系统线性方程,采样时刻k时,车辆控制输入序列U(k)与预测输出序列Y(k+1|k)如下

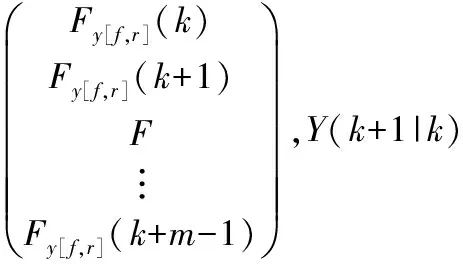
(16)

因此,经过p次运算后的输出预测如下

Y(k+1|k)=Sxx(k)+Su,fU(k)f+Su,rU(k)r

(17)

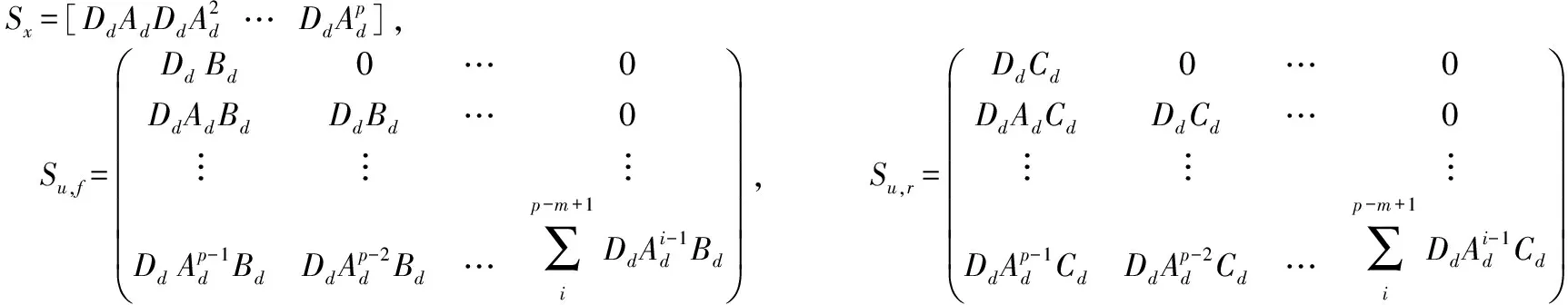
3 仿真与分析

对上文所述系统通过CarSim/SIMULINK联合仿真。利用CarSim的整车模型和精确的轮胎模型,在SIMULINK中搭建仿真模型,采用表1中车辆基本参数。

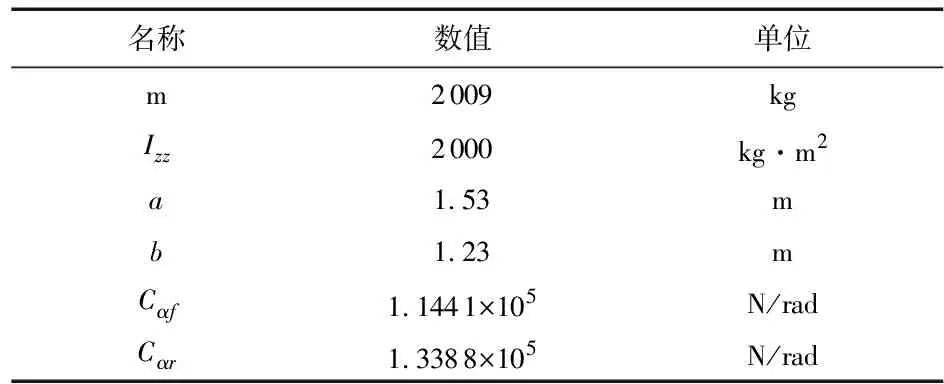
表1 车辆基本参数表

设定车辆在60 km/h恒定车速下进行仿真。本文对三种不同情况进行仿真试验：t=0 s时输入障碍物信息；在t=16 s时输入障碍物信息；有障碍物在t=17 s时输入障碍物信息。并对比了t=0时、t=16时与t=0时、t=17时车辆避障过程中的稳定性。如图4(a)所示。

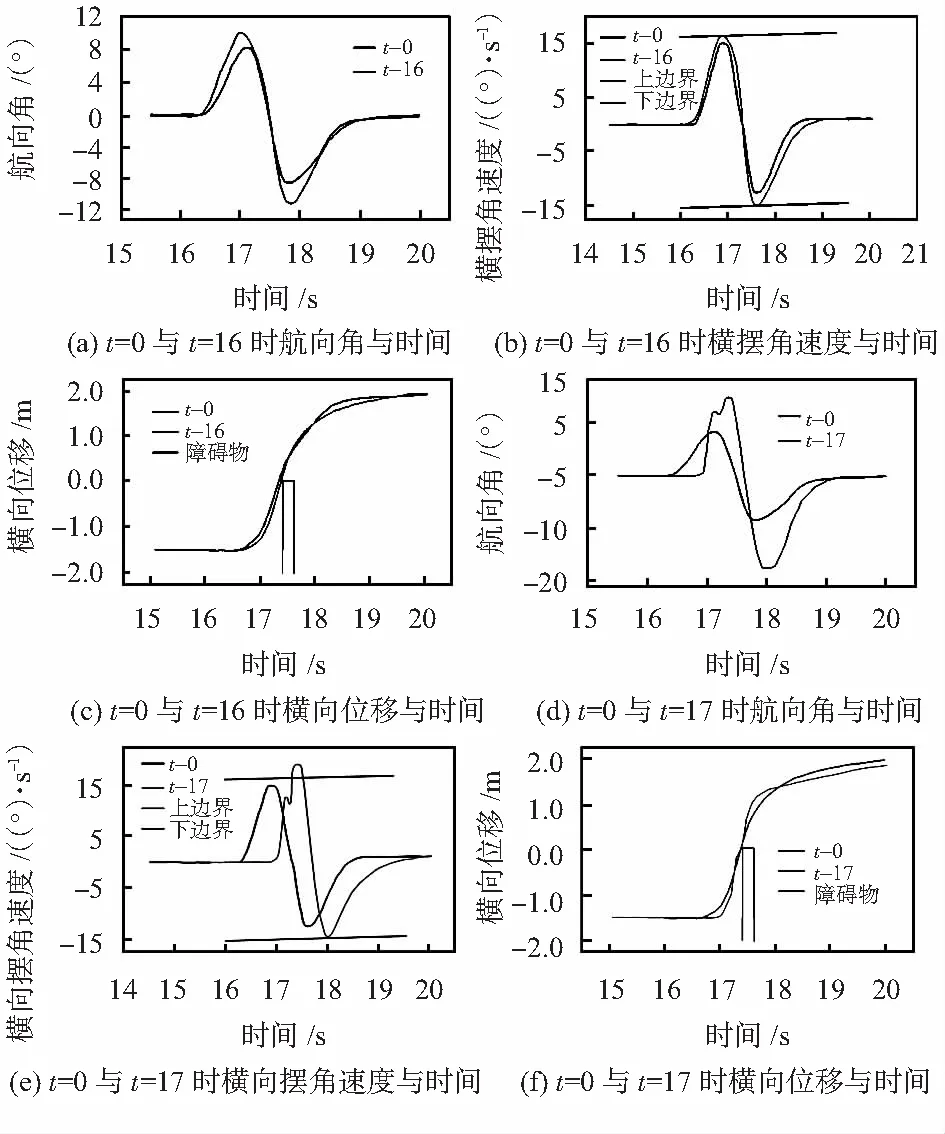
图4 仿真结果

由图4(a)～(c)所示。当t=0时输入障碍物信息,车辆因与障碍物还有一定的距离,其大于安全距离。车辆有较长的距离去实现避障,因此其主要约束就在其稳定性上。由图4(b)可知,车辆在避障过程中,横摆角速度已经接近理论极限值,但在允许范围内。证明本文设计控制能够使车辆平稳的避开障碍物。当t=16时输入障碍物信息。车辆与障碍物的距离等于安全距离,所以导致车辆必须立即开始避障,因此避障第一优先级开始约束。在图4(b)中,车辆的横摆角速度部分超过约束值。但车辆完成避障后,稳定性开始约束。因此在控制器调控下,其又回归到极限值以内。

由图4(d)～图4(f)所示,在障碍物信息输入之前,车辆沿直线行走。在t=17 s时输入障碍物信息,车辆与障碍物距离小于安全距离。其类似于车辆在道路上行驶突遇紧急车况,控制器迅速预测避障路径。t=17.5 s前后,控制器已经违反了稳定性原则,来实现避障的效果。在车辆安全避开障碍物以后,控制器又重新加入稳定性约束。因此横摆角速度回归到极限值以内,并在之后没有再违反。因为此时车辆已经避开障碍物,控制器只需要控制其满足稳定性原则即可。