基于改进极限学习机的三轴加速度计误差补偿算法*

刘艳霞， 方建军， 石 岗

(1.北京联合大学 城市轨道交通与物流学院，北京100101；2.中国石油大学(华东)信息与控制工程学院，山东 青岛 266580)

0 引 言

加速度计是惯性导航的关键部件，其输出精度直接影响惯性导航系统的精度[1]。石英挠性加速度计是加速度计中最重要的一种。其中，霍尼韦尔QA-160T型石英挠性加速度计具有机械性能稳定、内耗小、迟滞小、漂移小，价格低等优势，广泛应用于机器人位姿控制、惯性导航等领域[2]。加速度传感器的精度一般由制造精度和标定精度两方面决定。制造精度目前已基本接近极限，进一步的提高需要耗费很大的人力物力。因此，提高误差标定和补偿精度就显得尤为重要。

文献[3]通过对石英加速度计的动态性能测试，发现其误差主要包括偏差常量、周期性误差和高斯噪声。文献[4,5]利用椭球假设法的三轴加速度计误差进行标定和补偿，数据采集对传感器姿态要求不高，但搜索最优解的速度较慢。文献[6]利用最小二乘法估计确定性误差校准系数，但需要依赖载体姿态(横滚角和俯仰角)获取实际加速度作为参考。文献[7]采用分步校准法，对加速度计误差进行补偿，其实质和椭球拟合法类似。文献[8～11]分别采用6位置、10位置、12位置和24位置等位置翻滚标定法来解算误差系数矩阵中的未知量。文献[12]通过BP神经网络补偿加速度计误差，补偿后输出最大误差绝对值由0.457 5gn减少到0.0701 4gn，降低一个数量级。

本文针对三轴加速度计存在的测量误差，建立了隐式非线性误差模型,并提出一种改进的极限学习机——自主反向调优极限学习机(auto reverse tuning extreme learning machine,RT-ELM)对误差模型进行训练。该方法的训练速度是传统神经网络的数千倍，加速度计补偿后误差可下降150倍左右。

1 三轴加速度计误差分析

因加工工艺所限，三轴加速度计在制造过程中难免会产生零点偏差、三轴灵敏度不一致误差和三轴不正交误差[4]。

零点偏差指无加速度输入时，因制造误差加速度计也会有一定非零伏的输出电压[4]。灵敏度误差是指实际加速度计各轴的灵敏度都不同程度地和标称值之间存在一些偏差，即各种分量相等时三轴加速度计的输出也未必完全一致，灵敏度矩阵不等于单位矩阵[4]。三轴不正交误差则是指加速度计的三个敏感轴并非两两严格正交，实际上其敏感轴通常会偏离理想正交坐标系微小的角度，如图1所示，这将带来加速度测量的非线性误差[12]。

图1 三轴加速度计不正交误差

正交坐标系Pm的Xm轴和加速度计坐标系Pb的Xb轴完全重合，Ym轴和加速度传感器Xb,Yb轴在同一平面，它们之间的夹角分别为∂,β和γ。

这些综合因素为三轴加速度计误差校准和补偿带来很大的挑战，传统的显示误差模型难以充分表达测量过程中存在的非线性误差。本文建立了非线性隐式误差模型，并提出一种自主反向调优的超限学习算法对模型进行训练。

2 基于极限学习机算法的非线性误差模型辨识

新加坡南洋理工大学黄广斌教授在对单隐层反馈神经网络进行了深入研究的基础上，提出了极限学习机(extreme learning machine,ELM)[13]和传统反向传播(back propagation,BP)神经网络相比，ELM网络缺少输出层偏置，而且输入权重wij和隐含层偏置bi随机产生不需要调整，整个网络仅剩下输出权重βki需要确定。

假设隐含层有L个神经元，训练集包含N个不同样本(xi,yi)，其中，输入xi=(xi1,xi2,…,xin)∈Rn，输出yi=(yi1,yi2,…,yim)∈Rm，若采用非线性激励函数g(x)，可以零误差逼近来自同一连续系统的N个输入样本，使得

(1)

式中wi=(wi1,wi2,…,win)，xj=(x1j,x2j,…,xnj)T。 式(1)可改写为

Y=Hβ

(2)

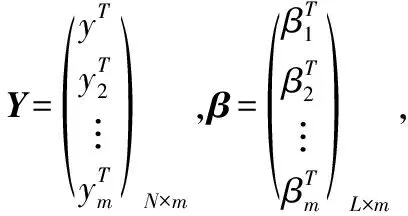
令ELM网络的输出等于样本标签T如式(3)所示

T=Y=Hβ

(3)

多数情况下，隐含层神经元的个数L远远小于训练样本的个数N，因此式(3)的解为使损失函数C最小的解

(4)

根据最小范数解准则，式(4)存在极小范数最小二乘解

(5)

式中H+为输出矩阵H的广义逆。

3 RT-ELM算法

虽然上述固定型极限学习机具有速度快，无需迭代，不易陷入局部最优等特点，但已证明隐含层节点数对网络性能具有很大影响[12]。然而，隐含层节点数只能凭经验选择，如何确定最优节点个数是个难题，当前主要集中在增量型极限学习机研究上。

3.1 三轴加速度计非线性误差模型

增量型极限学习机的隐层神经元数随着迭代过程逐次递增，已经被证明第k+1次迭代所获得的网络(具有k+1个隐含层神经元)输出误差小于第k次迭代所获得的网络输出误差，解决了隐含层节点选择难的问题。但k+1个隐含层神经元中有很多神经元的输出权值Wij很小，也就是说这些神经元对最终网络输出起到的影响很小，若能减少这些“无用”的神经元，就能大大减小增量型极限学习机的迭代次数，提高学习效率[13]。但减少“无用”的神经元，也必然在一定程度上导致网络误差有所增加。本文借鉴深度学习算法中连接权值反向调优思想，提出一种RT-ELM误差模型训练方法，误差网络模型如图2所示。

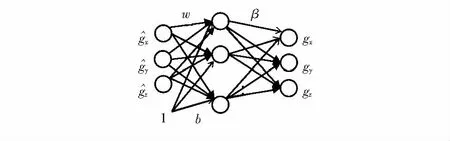
图2 三轴加速度计误差模型

3.2 误差模型训练方法

模型训练包括2个阶段：1)随机初始化输入连接权值wij和bi，根据公式计算输出连接权值βki；2)根据网络残差，借鉴深度学习反向调优对连接权值进行反向微调。

根据反向调优结果更新网络代价函数，若小于期望值，或迭代次数超过预定值K，则训练结束；否则返回到前面步骤继续。网络训练流程如图3所示。

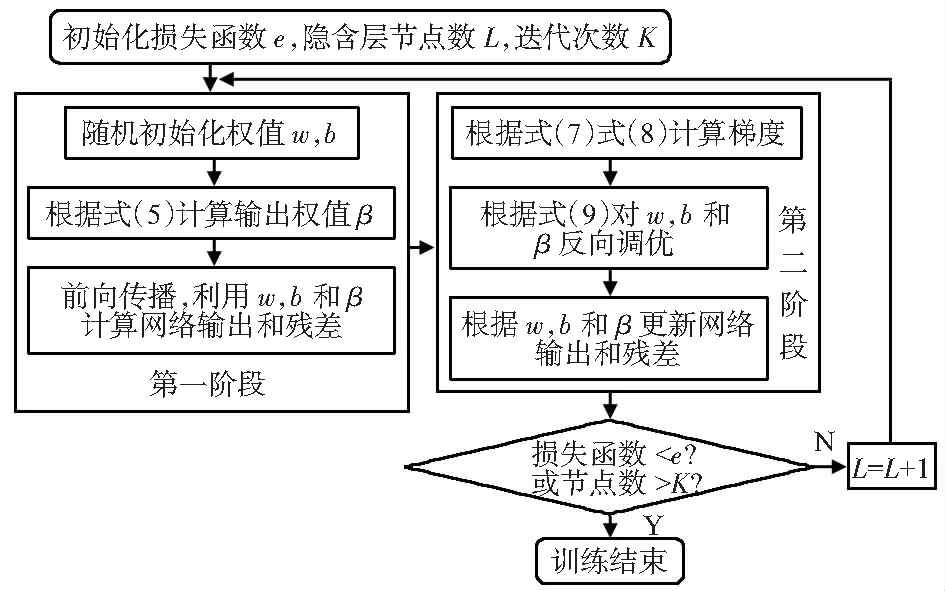
图3 RT-ELM训练流程

当N为奇数时，执行第一阶段。首先随机初始化输入连接权值wij和bi；再根据式(5)计算输出连接权值βki；然后根据得到的网络连接权值进行前向传播，计算网络输出和网络残差。

当N为偶数时，执行第二阶段。首先根据第一阶段得到的连接权值,wij,bi和βki，通过前向传播得到磁罗盘测量值对应的网络输出；然后计算网络输出与磁罗盘参考值之间偏差，即为网络残差err。假设网络各层的激活值分别为a1,a2和a3，网络损失函数为e。反向调优的目的就是为了减小损失函数e，为此需要求损失函数对连接权值的偏导。求解过程如下：

1)前向传播过程中，各层的激活值为

(6)

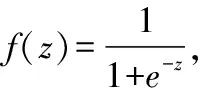
2)通过反向求导计算所需的第二层和第三层残差

(7)

3)输入层和输出层的梯度为

(8)

4)利用梯度下降法进行反向调优

(9)

4 误差补偿实验

为验证固定型ELM和改进后RT-ELM的误差补偿效果，用自行研制的三轴加速度计在翻转六面体上进行实验，如图4所示。

图4 翻转六面体

三轴加速度计固定在六面体上，通过上下左右翻转，采集不同位姿时x,y,z三轴的加速度，本次实验共采集2 969个样本点。样本标签取垂直地面方向轴为重力加速度，平行地面方向加速度为0。从2 969个样本中任意取2 000作为训练集，对图2所示的非线性误差模型进行训练；其余的969个样本作为测试集，用于测试训练得到的误差模型性能，结果如图5所示，固定型ELM用时0.015 4 s，改进的RT-ELM用时0.061 5 s。图5(a)为改进ELM算法前后x轴加速度计误差对比情况，固定型极限学习机ELM补偿后最大误差为0.025 m/s2，均方根误差0.026 6 m/s2；RT-ELM补偿后最大误差为0.007 m/s2，均方根误差0.003 7 m/s2。RT-ELM算法补偿后比补偿前的均方根误差0.559 9 m/s2减小了151倍，比固定型ELM算法减小7.2倍。

图5(b)为改进ELM算法前后y轴加速度计误差对比情况，固定型ELM补偿后最大误差为0.042 m/s2，均方根误差0.008 0 m/s2；RT-ELM补偿后最大误差为0.01 m/s2，均方根误差0.003 4 m/s2。RT-ELM算法补偿后比补偿前的均方根误差0.541 9 m/s2减小了159倍，比固定型ELM算法减小2.4倍。

图5(c)为改进ELM算法前后z轴加速度计误差对比情况，固定型超限学习机ELM补偿后最大误差为0.045 m/s2，均方根误差0.027 0 m/s2；RT-ELM补偿后最大误差为0.007 m/s2，均方根误差0.003 8 m/s2。RT-ELM算法补偿后比补偿前的均方根误差0.387 2 m/s2减小了102倍，比固定型ELM算法减小7.1倍。

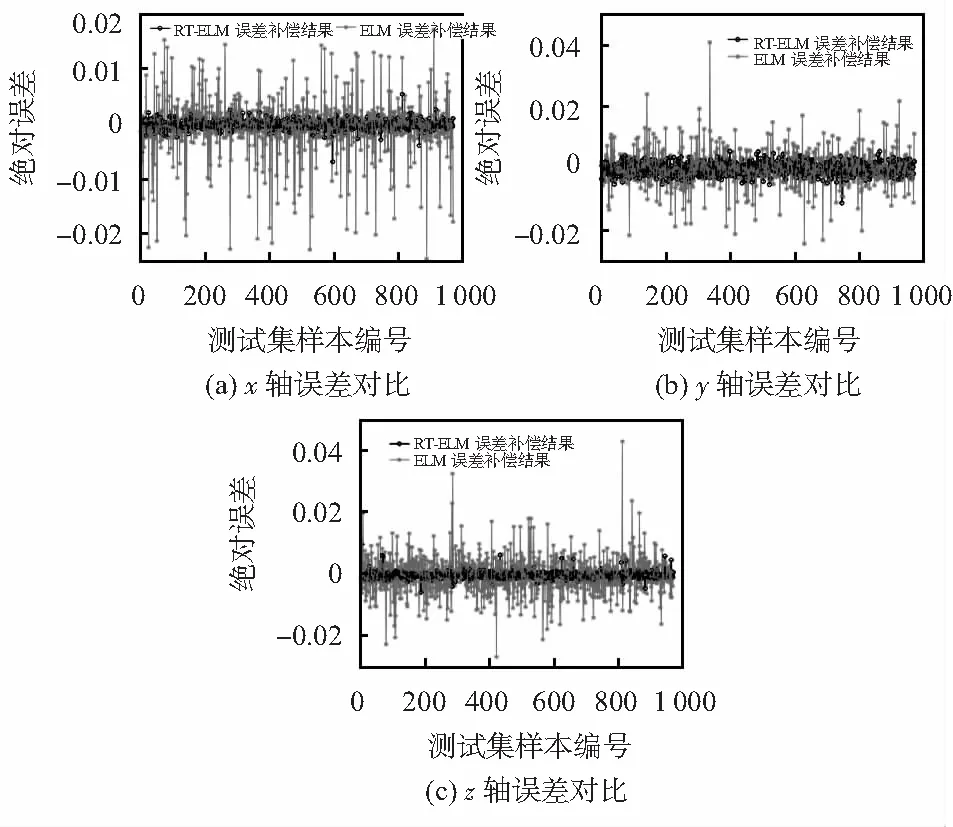
图5 改进ELM算法前后加速度计误差对比

5 结 论

在误差补偿实验中，对近3 000样本的数据集进行随机抽取训练集和测试集，反复多次，误差补偿结果基本都在±0.07 m/s2范围内，均方根误差小于0.004 m/s2，误差比补偿前减小超过100倍，可见超限学习算法不仅具有出色的补偿效果，还具有很强的泛化能力。固定型ELM算法无需迭代训练，速度极快，几千个样本的数据集训练速度为0.015 s；基于RT-ELM算法，因为对隐含层节点个数需要迭代寻优，用时约0.06 s。虽然基于RT-ELM比固定型ELM耗时增加了3倍，但依然是毫秒(ms)级的，精度也有明显提升。因此，该算法不仅可以提高三轴磁传感器误差补偿精度，还可用于其他对实时性要求较高的误差补偿和控制领域。