基于视觉原理的高精度6D传感器设计*

赵子越， 甘晓川， 马骊群

(中国航空工业集团公司北京长城计量测试技术研究所，北京 100095)

0 引 言

在大型装备制造业中的测量任务复杂多样性的特点导致单一的坐标测量难以满足需求，还需要6D参数(3个旋转角：俯仰角、滚转角、偏航角和3个位移量X,Y,Z)的高精度测量[1,2]。例如，在飞机轮船等大部件对接、机器人智能制造、自动导引车(automatic guided vehicle,AGV)引导等过程中，需要实时监控被测对象的6D参数，达到精度控制和准确引导的目的[3]。因此，6D传感器设计成为一项热点技术,引起众多研究[4,5]。在国外，海克斯康公司研制了配合激光跟踪仪的6D测头T-mac，测角精度可达0.01°，但是成本较高，且关键技术对国内垄断。在国内，天津大学的邾继贵教授团队研制了基于室内GPS的6D传感器，可配合室内GPS使用，在工程上具备一定的应用基础，但成本略高[6]。目前，基于视觉原理的6D传感器可通过高精度校准手段保证精度，通过图像处理技术保证效率，同时相机成本较低，诸多优势使得视觉原理的6D传感器成为解决现场条件下6D参数测量的首选[7,8]。但基于视觉原理的6D传感器往往因为目标点约束不合理导致测量精度不高。

本文从设计方案出发，探讨目标点的数量和位置对测量结果的影响以确定目标点的最佳个数与位置；选择红外发光目标减少现场干扰；利用双经纬仪系统对传感器进行校准以保证结构参数精度；设计6D参数的高精度迭代解算方法，采用拉格朗日乘子法解决迭代初值；最后通过实验验证了6D传感器的测量精度。

1 高精度6D传感器设计

考虑发光点目标需具备高精度和高识别的特点， 6D传感器主要包括多个主动发光点、电路及其相应电器原件、机械金属构架等。

1.1 目标点的数量

目标点的数目与测量原理相关，对应解的个数如下：当n=3时，且目标点所确定的平面不通过光心，最多有4组解。当n=4且不共面时，最多有5组解；当4个点共面时，可唯一线性求解。当n=5时，且任3点不共线，最多有2组解。当n≥6时，可唯一线性求解。考虑到过多的点会影响算法的效率，同时对精度的提高不显著，本传感器采用6个目标点，其中4个共面。

1.2 目标点的分布

目标点分布依据三点不共线、四点不共面、点的包络空间在平面和纵深方向比例一致的原则。系统采用一般工业相机的测量距离为2～5 m，相机的成像尺寸约为200 mm×200 mm，6D传感器目标点的间隔应大于成像尺寸的2/3,即目标点包络立体空间应不小于120 mm×120 mm×120 mm。

1.3 目标点的形状、感光及抗噪特性

目标点形状按约束特征标记区分为点、圆、球、直线等，其中球和圆、线等特征在图像处理时难以提取且精度不高。本文选取的点特征可在克服背景干扰的情况下可以进行快速提取，适合于实时测量。理想目标点明暗对比强烈，不同视角光斑形状变化小，受背景光干扰小。经比较选用Honeywell公司的IrLED，型号为SE3470—002，其发光材料为AlGaAs，发射窗口为平面窗口[9]。

1.4 金属构架结构设计

6D传感器结构如图1所示，机械构架分为背板组件和底板组件，定义背板尺寸为210 mm×230 mm，安装4个红外LED发光目标点，横向间距为160 mm，纵向间距为150 mm；定义底板尺寸为210 mm×230 mm，安装有2个红外LED发光目标点，横向间距为150 mm。

图1 6D传感器结构设计

1.5 目标点安装组件

为提高目标点与金属构架的定位精度，设计了用于安装并定位目标点的精加工安装座。考虑到目标点器件为金属外壳，为保证绝缘，目标点安装座的材料选用黑尼龙。首先将目标点器件安装进尼龙安装座并粘胶固定，然后以尼龙安装座定位面为安装面，整体安装进具有相同加工精度的金属构架目标安装孔，利用机械定位将目标中心安装至系统要求的预定位置。

1.6 电源供电

实验中发现纽扣电池直接供电无法保证电流的稳定，其电流值会以较快的速度衰减，这严重影响6D传感器的性能和精度，本文采用北京大华公司DH1718E型稳压稳流电源供电。

2 6D传感器校准方法

图2为6D传感器：结构参数标准，其过程是获取6个目标点在传感器坐标系下的精确坐标，采用经纬仪组网进行校准。

图2 6D传感器结构参数校准

具体过程：采用2台Leica的TM5100型号经纬仪组网，测量网不确定度为0.02 mm+0.02 Lmm/m，满足精度要求。在6D传感器背板及底板平面分别粘贴4个纸质目标点，在前凸台粘贴3个目标点。用双经纬仪逐个瞄准纸质目标点和6个LED目标点，瞄准时应保证经纬仪的瞄准镜中的瞄准环与目标点瞄准环或金属边缘重合或等距。根据纸质目标点创建两平面，从而确定两坐标轴方向，并以LED目标点P1点为原点创建6D坐标系，从而得到6D坐标系下所有点的坐标。结果如表2。

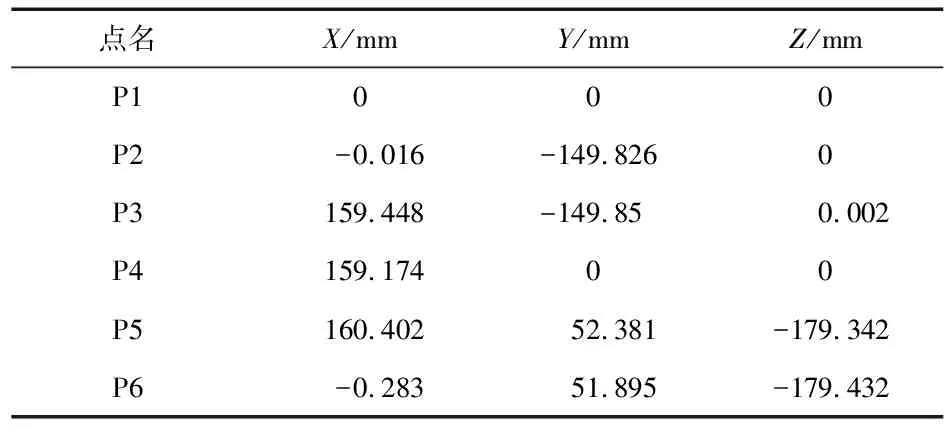
表1 6D传感器校准结果

3 6D传感器测量原理

3.1 6D参数解算模型

使用时6D传感器固定在被测件上，通过相机拍摄图像结合传感器坐标系下6个目标的坐标值解算被测件的6D参数。以单相机测量为例，由透视模型[10]可知，相机像素坐标系uov和传感器坐标系Ow-XwYwZw的关系可由以下公式表示

(1)

式中s为比例因子，(u,v)为像素坐标系下的值，(xw,yw,zw)为传感器坐标系下的值，矩阵A代表内参数，是3×3矩阵，可表示为

(2)

式中fx,fy,u0,v0为相机已知的内部参数。[RT]为外参数待求，R为旋转矩阵，T为平移向量，可表示为

(3)

式中R矩阵即可求解出物体坐标系分别绕x轴、y轴和z轴各自的旋转角度α,β和γ，连同T的沿x轴、y轴和z轴的平移参量，构成待求的6D参数，满足以下关系

R=Rz(γ)Ry(β)Rz(α)

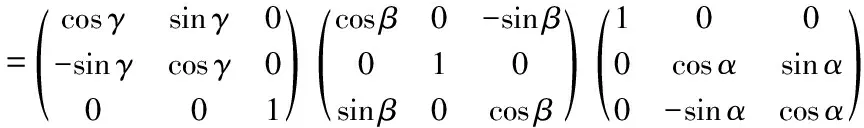
(4)

(5)

根据式(1)可以列以下约束方程组

(6)

式中fP为每个点的3个约束方程，考虑到R矩阵为正交矩阵，满足以下关系

(7)

未知数的个数减少为6个，6个目标共有18个约束，因此,可以采用罚函数法构建最优化目标函数求解

(8)

式中λ为惩罚因子。这种非线性最优化问题可用Levenberg—Marquardt(LM)算法进行求解，得到[RT]，完成6D参数求解。

3.2 迭代初值估计及目标函数求解方法

LM算法是非线性最小二乘算法，收敛速度快、算法稳定性好[11,12]。但采用LM算法必须采用合适的迭代初值，否则易造成迭代不收敛[13]。根据相机模型，约束方程可以写成以下的矩阵形式

AX=0

(9)

式中 矩阵A为一个18×13的系数矩阵。X=[r1r2r3r4r5r6r7r8r9txtytz]T作为未知的初值待求。将未知量X分解为X9=[r1r2r3r4r5r6txtytz]T和X3=[r7r8r9]T，则方程可写为

BX9+CX3=0

(10)

对式(10)进行求解，得到X3和X9,从而得到迭代初值。将迭代初值带入最终优化目标方程，即可得出6D参数。

4 精度验证实验

引入6D标准装置进行精度验证，该装置由航空工业计量所研制，由三轴转动和三轴平移机构组成。三轴直线运动机构由精密导轨提供支撑和导向，xyz三轴行程分别为1 000 mm×300 mm×300 mm，位置分辨率0.1 μm，位置定位精度±5 μm。三轴转动为正交结构转台，由角接触球轴承提供精密转动支撑，角度行程为180°×40°×40°，角度定位精度为±2″。

首先进行重复性测量实验，将6D传感器固定在空间的任意位置，采用相机进行重复性测量，得到结果如表2。

表2 6D传感器重复性性实验结果

由实验数据可知，三个旋转角α，β和γ的重复性精度分别为0.008°，0.006°和0.008°，三个平移参数x,y和z的重复性精度分别为0.012，0.015，0.013 mm。

为进一步验证精度，将6D传感器安装到6D标准装置上，实验现场如图3所示。

图3 精度对比实验

6D标准装置分别沿3个旋转轴和3个平移轴移动11个位置，计算出10个间隔值，以6D标准装置间隔值为真值，与传感器输出参数进行比对。

由实验数据可得，6D传感器的旋转角α在-45°～45°行程内的均方根误差为0.017°，旋转角β在-20°～20°行程内的均方根误差为0.013°, 旋转角γ在-20°～20°行程内的均方根误差为0.016°; 在X方向0～300 mm范围内均方根误差为0.077 mm，在Y方向0～200 mm范围内均方根误差为0.095 mm，在Z方向0～200 mm范围内均方根误差为0.079 mm。

5 结 论

针对现场条件6D参数高精度实时测量需求，设计一种基于视觉原理的6D传感器，从传感器结构、目标点数目及分布、目标材料等方面考虑；利用双经纬仪测量系统对传感器进行校准；研究了基于控制点的6D参数测量方法，在完成迭代初值获取的前提下采用LM法进行精确求解；最后采用6D标准装置进行了实验验证，实验结果证明：传感器旋转角α,β、和γ的重复性分别为0.008°，0.006°和0.008°，均方根误差分别为0.017°，0.013°和0.016°；三个平移参数x，y和z的重复性分别为0.012，0.015，0.013 mm，均方根误差分别为0.077，0.095，0.079 mm，具备较高的推广价值。