基于2D靶标的摄像机与转台中心轴同步标定方法*

吕海东， 任永潮， 戴士杰,， 王志平

(1.河北工业大学 河北省机器人感知与人机融合重点实验室,天津 300130；2.中国民航大学 天津市民用航空器适航与维修重点实验室,天津 300130)

0 引 言

叶片作为航空发动机的核心零部件，长期工作在高温、高压、高速旋转的环境中，极易产生疲劳损伤等破坏[1]。由于国内目前还没有针对叶片修复的成熟设备，对可修复损伤叶片的处理一般为国外送修，造成大量经济损失。为了打破国外技术封锁，研究具有自主知识产权的叶片测量与焊接一体化装备意义重大。叶片的堆焊修复过程需要在已知叶片三维外形的基础上进行[2]。由于光栅投影三维测量方式具有非接触、高精度等优点[3,4]，故采用该方法测量叶片三维外形。但是受到测量设备和环境等因素的限制，每次测量得到的点云数据只是实体叶片一个侧面，需要利用旋转平台等设备完成点云的拼接。

现有的利用转台进行点云测量与拼接的系统中，转台中心轴的标定工作，是完成点云拼接的关键一步。在旋转平台中心轴标定问题上，国内外学者做了大量研究。Park S Y[5]在多视角物体真实三维模型获取与拼接展开了相关研究，利用垂直于转台上的棋盘格标定板实现转台中心轴的标定。Ye Y[6]在三维点云测量与拼接系统中，提出一种利用L型标定块多角度点云测量，处理垂直于转台的点云完成中心轴标定的标定方法，该方法需要首先完成摄像机标定，至少处理两个相交面点云，导致标定效率不高。胡民政[7]提出一种在完成摄像机标定的基础上利用标定球完成对转台中心轴标定，该方法标定精度依赖图像处理算法，导致精度难于保证。周朗明[8]提出一种利用3片以上不同角度的位于圆柱面上的点云数据标定出旋转平台中心轴的位置，该方法也需要处理大量点云数据，导致标定效率不高。

在航空发动机叶片焊接修复的测量与拼接系统中，通过控制转台旋转实现对压气机叶片多个角度三维形貌的测量，利用转台中心轴在摄像机坐标系下的位置[9,10]，确定多角度测得点云数据之间的旋转平移矩阵，实现多视角点云拼接。本文提出一种基于2D靶标的摄像机与转台中心轴同步标定方法。将该方法应用于航空发动机叶片焊接修复系统中，对提高系统标定效率和精度具有重要意义。

1 光栅投影三维测量与点云拼接系统

由于经典光栅投影三维测量模型包含诸多难以达成的约束条件[11]，所以本文采用文献[11]提出的解除约束模型，如图1所示。该模型中采集到物点是摄像机坐标系下的三维坐标，要解出像点与物点之间的关系，需要完成摄像机标定来确定测量系统中的8个参数。正因为获取物体三维点云坐标属于摄像机坐标系下，所以只需标定出转台中心轴摄像机坐标系下的空间位置，即可根据转台中心轴确定不同视角下点云之间的旋转变换关系，完成多视角点云拼接。综上所述，压气机叶片测量与拼接系统不仅需要标定摄像机还需要标定转台中心轴。

2 标定模型分析

计算机视觉的基本任务之一是通过二维图像信息计算三维空间中物体几何信息，并由此重建和识别物体。而摄像机标定就是确定空间物体某点与图像中对应点之间关系的内外参数。针对传统摄像机标定法和自标定法[12]二者的缺点，张正友[13]通过对标定板不同角度采集图像实现对摄像机的标定的方法。

旋转中心轴线作为测量数据拼合的基准，在国内一般采用将标准件(标准件包括标准球、标准圆柱体、标准圆锥等)固定在旋转平台上，通过对标准件运动轨迹拟合圆并求出圆心所在的直线[14]。国外大都采用基于平面参照物的坐标变换求解出旋转中心轴线的空间位置[5]。

2.1 2D靶标摄像机标定模型

2D靶标摄像机成像模型中，图像像素坐标系下像点m(u,v)与该点对应的世界坐标系下物点W(Xw,Yw,Zw)的齐次坐标变换关系为

(1)

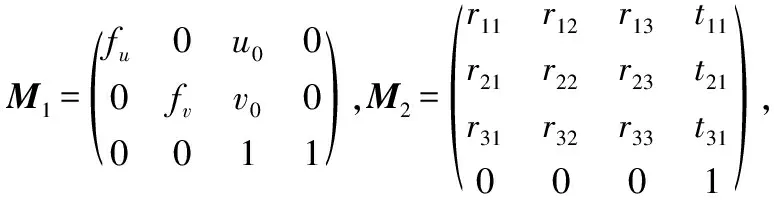
2.2 2D靶标转台中心轴标定模型

当平台围绕中心轴线旋转时，物体随转台转动，则物体上每个点运动轨迹必然在以旋转轴为中心的圆上，而处于不同平面S[s1,s2,…,sn]内的点P[p1,p2,…,pn]旋转形成的n个以O[o1,o2,…,on]为圆心的圆，位于旋转轴l的不同位置。利用如图2所示转台旋转特点和规律，通过测量这些轨迹上的点在摄像机坐标系中的坐标，分别将它们拟合成圆，求出所有拟合圆的圆心坐标，最后将这些圆心点拟合成直线，该直线即为旋转轴在摄像机坐标系下的位置方程。

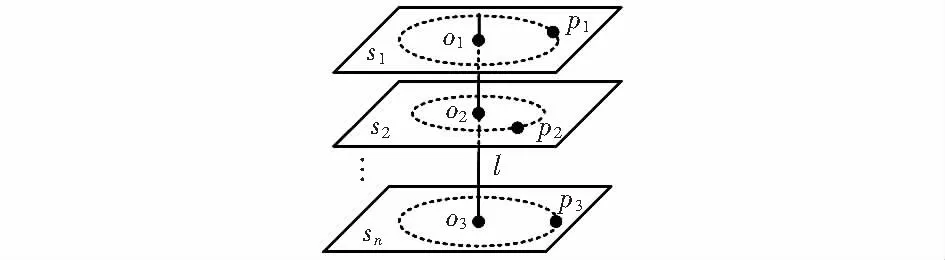
图2 转台中心轴标定原理

标定时，棋盘格标定板靶标坐标系与摄像机坐标系之间的关系如图3所示。

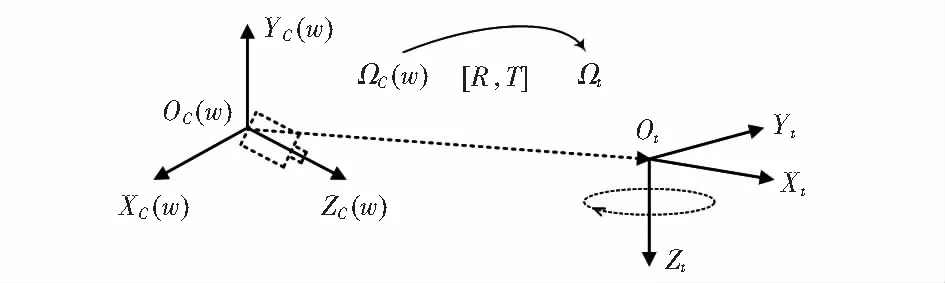
图3 摄像机坐标系与转台坐标系关系

图中Ωc坐标系为摄像机坐标系，Ωw坐标系为世界坐标系。其中，世界坐标系Ωw是用来描述1个固定场景中摄像机和旋转平台的位置。那么由于去约束模型中物体三维点云是在摄像机坐标下的坐标，为了统一系统模型，世界坐标系Ωw与摄像机坐标系Ωc重合。要求得旋转平台坐标系Ωt相对于世界坐标系Ωw的位置关系，只须求出旋转平台坐标系Ωt相对于摄像机坐标系Ωc的位置关系即可，其中[R,T]为旋转平移矩阵。

得到两个坐标系之间的变换关系如下

(2)

式中Ri为标定板靶标坐标系到摄像机坐标系的旋转矩阵，Ti为平移矩阵，i为标定板靶标的位置序号。

根据2D标靶的摄像机标定方法，只要获取多于两个位置的平面靶标图像就可以求取摄像机的内外参数。当获得了摄像机的内外参数后，根据式(2)和Zt=0可以推出

(3)

由此求得，像素坐标系中点(xb,yb)在世界坐标系下的三维坐标(Xc(w),Yc(w),Zc(w))。分别将不同位姿时同一角点的世界坐标拟合成圆并求取圆心坐标，最后将这些圆心拟合成直线，得到旋转轴在摄像机坐标系下的直线方程，完成标定。

3 同步标定流程

通过分别对基于2D靶标的摄像机与转台中心轴标定方法分析，可通过利用转台旋转调整2D靶标位姿，摄像机采集一组图像，一次性处理数据，同步完成两个标定过程。同步标定过程如图4所示。

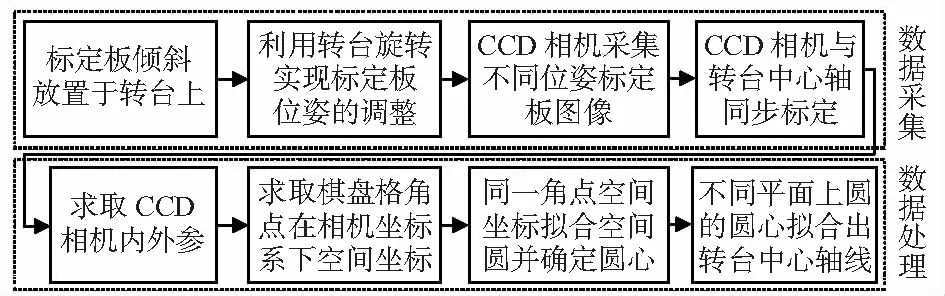
图4 同步标定流程

具体标定过程如下：1)将摄像机与旋转平台安装于光学实验平台上固定；2)将棋盘格平面标定板倾斜放置于旋转平台上，以摄像机采集图像范围进行角度调整(60°～80°为宜)；3)控制旋转平台旋转一定角度(10°～15°)，由于标定板只有一个面有棋盘格图像，应避免因旋转角度不当造成标定板背对摄像机导致采集图像失效的情况；4)转台旋转一个角度后，摄像机采集一幅图像。重复上述步骤便得到一系列标定板不同位姿图像；5)求取每个位姿时靶标相对于摄像机坐标系的旋转平移矩阵，根据2D靶标中心轴标定原理完成中心轴标定。

4 实验与结果分析

4.1 实验设备

为验证本文所提方法的可靠性，利用如图5所示实验设备，其中，摄像机为德国SVS-VISTEK公司的SVCam-ECO267，其分辨率为1 360像素×1 024像素；镜头为日本Computar公司的M3Z1228C-MP；标定模版采用7×9阶平面棋盘格标定板，棋盘格宽度为15 mm；直径为38.071 3 mm标准球，形状误差为0.002 8 mm；软件平台为MATLAB 2014。

图5 实验设备

4.2 摄像机与转台中心轴标定

按照同步标定步骤，采集10幅标定板不同位姿图像，如图6所示。

图6 标定板不同位姿图像

得到摄像机与标定模板相对位置关系如图7，可以看出棋盘格标定板相对静止，摄像机围绕标定板做圆周运动。

图7 摄像机与标定模板相对位置关系

由于标定过程只提取了棋盘格标定板内部48个角点，随机提取标定板上坐标为(15,15)(30,30)(45,45)(45,60)(60,60)(75,75)(90,30)(90,45)(90,60)(90,90)的10个角点各个位姿下的空间三维坐标，对每组空间点进行空间圆的拟合，并求取空间圆心坐标，根据圆心坐标拟合确定旋转中心轴的空间直线方程，如图8所示。确定的旋转中心轴的空间方程为

(4)

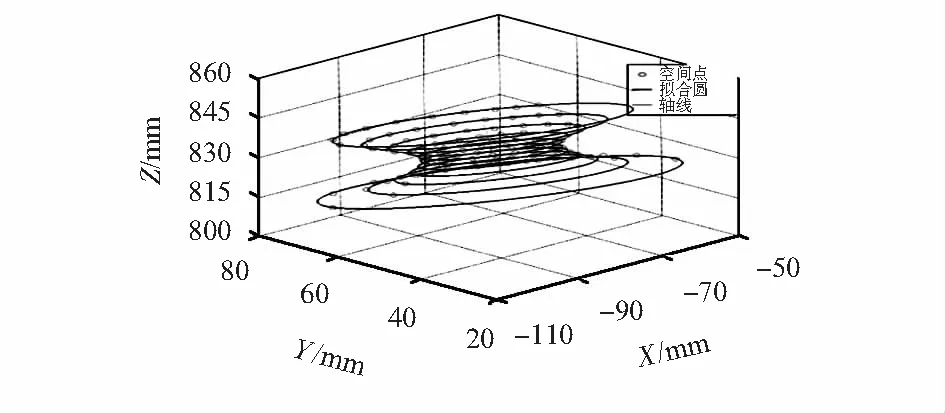
图8 转台中心轴空间位置

为了对比同步标定与分别标定效率，按照标准的标定流程，采集1幅图像需要5 s。分步标定实验中两个标定步骤分别需要采集10幅棋盘格图像，分别处理实验数据用时41.08 s。同步标定需要一次性采集旋转变换的棋盘格图像，一次处理实验数据需要32.73 s。对比如表1所示，同步标定用时较分步标定省时接近1 min。

表1 同步标定与分步标定对比

4.3 标准球测量与拼接实验

为验证本文方法标定旋转中心轴的可靠性，利用光栅投影测量与拼接系统，通过旋转平台顺时针旋转0°,90°,180°,270°，分别获取标准球体的四个角度的球面点云数据，如图9所示。

图9 标准球体四视角点云

以转台位于0°时获取的点云数据为基准，根据求取转台旋转中心轴的空间直线方程式(4)，求解三个绕转台中心轴反向(逆时针为正)旋转90°、180°、270°的矩阵分别为

M(90°)=

M(180°)=

M(270°)=

对相应点云数据旋转变换，将其变换至与基准点云相同的坐标系下，实现标准球四角度点云拼接，结果如图10。

图10 点云拼接结果

为了检测拼接效果，沿旋转中心轴线方向等间距提取拼接后的点云数据截面线如图11(a)所示。其中第7层截面线如图11(b)所示。其点云重叠部分径向偏差d在0.073 mm以内。

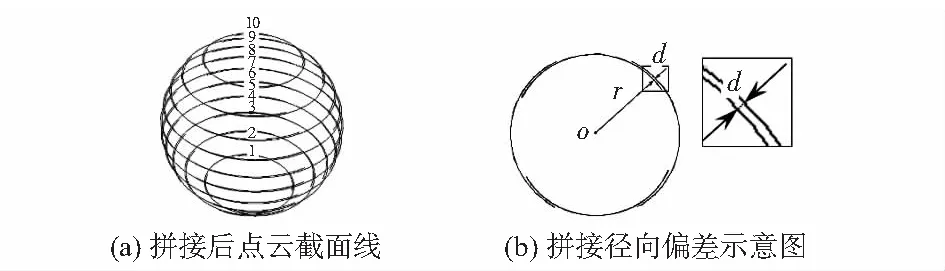
图11 拼接结果检测

为进一步检测拼接效果，将拼接后点云数据重合部分进行融合处理，对处理后的点云进行标准球模型重建，并选取模型3个视角进行直径检测，重建及直径D测量结果如图12所示。

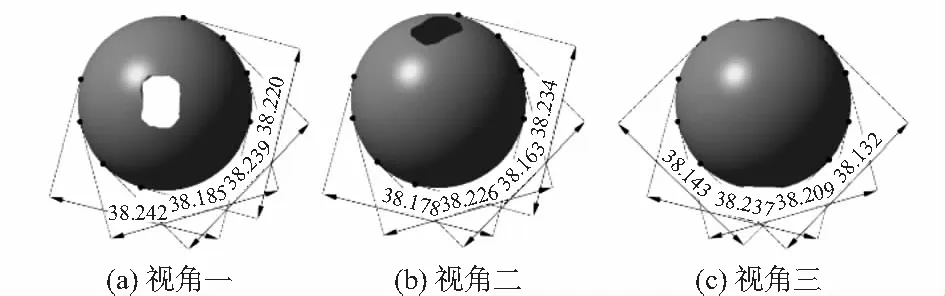
图12 标准球模型重建及直径检测

根据拼接后点云重建的标准球体模型直径与标准球实际直径偏差均值为0.129 3 mm。试验结果表明，通过旋转中心轴拼接的三维点云数据能够准确反映待测物整体尺寸信息，保证拼接后误差在0.2 mm以内。

4.4 叶片测量与拼接实验

根据标准球实验流程，获取如图13所示的4个角度点云数据。

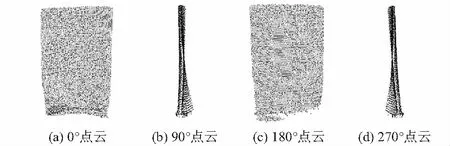
图13 叶片四视角点云

同理，以转台位于0°时获取的点云数据为基准点云，通过对相应点云数据的旋转变换，实现叶片四角度点云拼接，拼接结果如图14(a)所示。为了验证叶片拼接效果，选取距离叶片顶部10 mm等间距5个测量点通过对实际叶片测量厚度与拼接后的厚度对比，模型测量结果如图14(b)所示。测量结果对比如表2所示，平均偏差在0.119 2 mm，平均偏差率为4.47 %。拼接结果满足叶片堆焊修复需求[15]。

图14 叶片拼接及模型厚度测量结果

5 结 论

同步完成了系统摄像机及转台中心轴标定，较分步标定效率提升明显。在标准球四视角点云拼接试验中，拼接后点云重建的标准球模型直径与标准球实际直径偏差均值为0.129 3 mm；在航空压气机叶片四视角点云拼接试验中，拼接后获得叶片模型厚度与叶片实际厚度偏差的均值为0.119 2 mm，平均偏差率为4.47 %，满足叶片焊接轨迹规划的需要。所提方法通过一次性图像采集和处理，同步完成两个标定过程，有利于航空发动机压气机叶片三维测量及焊接修复轨迹规划的工业化应用。

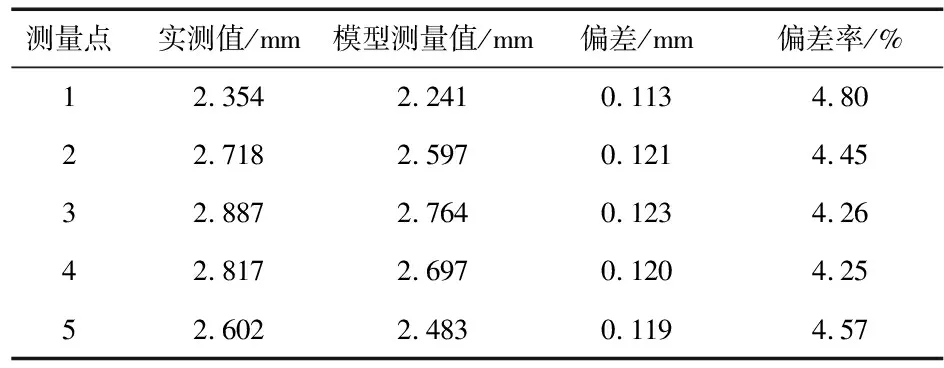
表2 叶片厚度实测值与模型测量值