基于弹性地基梁原理的铁路单箱单室曲线结合梁畸变效应分析

2019-06-25林2张彦玲

石家庄铁道大学学报(自然科学版) 2019年2期

邱爽，柳逊，余林2，张彦玲

(1.石家庄铁道大学土木工程学院, 河北石家庄 050043；2.中铁二十四局集团安徽工程有限公司，安徽合肥 230000 )

钢-混凝土结合梁具有自重轻，承载力大，建筑高度小，施工方便等优点，在高铁桥梁中已得到了大量应用。由于线路线形的需要，结合梁经常被布置为平面曲线，但由此也带来了弯扭耦合的问题。曲线结合梁大多采用无支架施工，由于钢梁壁厚较薄，既存在使施工阶段的曲线开口裸钢梁发生弯扭屈曲的风险，也容易使混凝土板结硬后的闭口箱梁截面产生明显的畸变效应，因此需设置适当的横隔板或横向连接系。

目前，对于闭口箱梁畸变效应的分析方法主要包括解析法、数值法和弹性地基梁比拟法。徐勋等[1]考虑剪切变形的影响，采用能量法推导了薄壁箱梁的畸变效应；Sakai et al[2]、张莉[3]、Park et al[4-5]分别采用解析法和有限元法分析曲线闭口钢箱梁的畸变效应，并采用图表法给出了对应于一定畸变应力比的最大横隔板间距；Yao et al[6-7]则采用弹性地基梁法分析了闭口钢箱梁的畸变效应，但以上报道大多针对闭口钢梁截面，专门针对闭口组合截面的研究较少。首先，现阶段闭口截面结合梁分析常用的乌曼斯基理论，虽然理论方法简单、适用性强，但其适用前提条件中忽略了闭口薄壁截面外轮廓线的变形，即忽略了畸变效应，所以造成计算结果偏差较大；其次，目前关于直线结合梁偏心荷载作用下的畸变效应分析研究较多，针对曲线结合梁较少；且现阶段多是通过有限元软件，分析在假定的隔板数下，相应的闭口截面结合梁的畸变效应，但对于从理论上推导满足畸变效应的横隔板间距控制公式较少。

本文针对混凝土结硬后的钢-混凝土单箱单室闭口曲线结合梁，首先采用M/r法将其转化为等效直梁，然后考虑钢梁与混凝土板的材料差异，根据常截面曲线结合梁的畸变控制微分方程，采用基于弹性地基梁原理的有限元法对曲线结合梁的畸变效应进行计算，并通过参数分析对单箱单室闭口曲线结合梁的横隔板布置给出建议。

1 基于弹性地基梁原理的闭口曲线结合梁有限元模型

1.1 基于M/r法的模型简化及荷载分解

目前应用于高速铁路桥梁的结合梁截面通常包括单箱单室截面(单线)，双箱单室截面(双线)及单箱双室截面(双线)，其中双箱单室截面可看作由2个单箱单室截面组成，每个单箱承受一线铁路活载。而双线单箱双室截面在扭矩作用下存在一次和二次畸变效应[8]，与单箱单室截面不同。本文的研究对象仅限于单箱单室曲线结合梁，双线单箱双室截面曲线结合梁将在后续进行研究。

所研究的单箱单室简支曲线结合梁及其截面见图1所示，两侧简支端均设置抗扭支座，属于简支超静定结构。沿梁轴方向设置若干横隔板，钢梁与混凝土板之间焊接圆柱头栓钉。

图1 曲线结合梁图示

M/r法是Tung和Fountain在 1970年给出的一种对曲梁进行扭转分析的实用简便的近似方法，其原理是将曲梁展开为直梁，将梁轴曲率的影响模拟为外加分布扭矩m(z)施加在等效直梁上，具体步骤见文献[9]，此处不再赘述。当等效直梁承受分布扭矩m(z)时，可将其进一步转化为作用在直梁上的水平反对称荷载，并分解成刚性周边不变形的纯扭转荷载和自相平衡的畸变荷载。图2为任一截面处扭转荷载的分解(图中箱型截面的上翼缘是指混凝土板)。

图2 任一截面扭转荷载分解图示

图2中,P(z)=m(z)/h，P1′(z)=-P3′(z)=-P1(z)=P3(z)=m(z)/(2b)，b为组合梁下翼缘宽度；P4′(z)=-P2′(z)=-P2(z)=P4(z)=m(z)/(2h) ，h为组合梁上、下翼缘中线之间的距离。

1.2 畸变控制微分方程

本文拟采用弹性地基梁比拟法分析混凝土结硬后闭口曲线结合梁的畸变效应。由于结合梁由不同的材料组成，不能直接采用以往单一材料的钢箱梁或混凝土箱梁中的畸变常数计算公式，故在文献[10]中以图1中角点1的畸变角γ1为基本未知量，考虑钢梁和混凝土板的材料差异，采用符拉索夫理论和能量法推导了闭口结合梁的畸变控制微分方程，得到了相应的畸变常数表达式。采用M/r法将常截面曲线结合梁展开为等效直梁后，其畸变控制微分方程为[10]

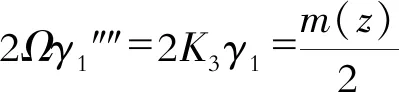
(1)

式中，2Ω为组合梁畸变翘曲惯性矩；2K3为组合梁的畸变框架刚度。畸变双力矩BA可定义为

BA=-2Ωγ1″

(2)

则畸变应力为

(3)

1.3 基于弹性地基梁原理的有限元模型

式(1)所示的结合梁畸变控制微分方程与弹性地基梁挠曲控制微分方程EIby″″+Ky=q在形式上完全相似，其中，弹性地基梁抗弯刚度EIb与结合梁畸变翘曲惯矩2Ω、弹性地基梁模数K与结合梁畸变框架刚度2K3、弹性地基梁均布荷载集度q与结合梁畸变水平分力偶m(z)/2、弹性地基梁挠度y与结合梁畸变角γ1、弹性地基梁弯矩M与结合梁畸变双力矩BA之间分别存在对应关系。结合梁的横隔板可简化为简支支承[11]。

结合梁畸变控制微分方程中的畸变框架刚度2K3相当于弹性地基梁地基模数K，因此畸变框架刚度2K3可模拟为仅在竖向受压的分布弹性支承，横隔板用铰支承来代替。在有限元模型中，将分布弹性支承简化为单元节点处仅在竖向受压的集中弹性支承Kij[10]。

(4)

式中，ΔSi-1、ΔSi为相邻两单元的长度；2K3为组合箱梁畸变框架刚度。

在文献[10]中已通过与理论分析的对比对该有限元模型进行了验证。

2 闭口曲线结合梁畸变效应分析

2.1 算例

某铁路简支曲线结合梁计算跨度l=24 m，根据铁路桥梁线路设置要求，曲线半径r=2 000 m，列车行车速度取200 km/h。截面为图1所示的单箱单室截面。钢梁采用Q345qE钢，上翼缘宽度bt=600 mm，厚度tt=30 mm；腹板高度hw=2 340 mm，厚度tw=16 mm；下翼缘宽度bb=3 000 mm，厚度tb=30 mm。桥面板采用C50混凝土，宽度bc=6 500 mm，厚度hc=400 mm。两个支座处各设置一个端横隔板。

2.2 使用阶段荷载

混凝土结硬后截面形成组合作用，由组合截面承受的荷载包括二期恒载和活载。二期恒载主要包括线路设备的质量；活载考虑客运专线ZK标准活载及其竖向动力作用、离心力和横向摇摆力。ZK标准活载计算图示见图3[12]。

图3 ZK标准活载图示

采用M/r法，将图1所示的曲梁展开为直梁，不同荷载作用于等效直梁上的分布扭矩m(z)分别如下。

2.2.1 二期恒载qD

通过查阅资料，高速铁路曲线梁桥的二期恒载近似取为qD=130 kN/m，沿截面横向对称布置，在简支梁上产生的分布扭矩mqD(z)为

(5)

2.2.2 ZK标准活载及其相关效应

对于单箱单室截面结合梁，列车活载可只考虑单线活载，且沿截面横向对称布置，同时考虑其动力作用、离心力和横向摇摆力。

(1)ZK标准活载及其动力效应。按跨中产生最大畸变正应力的原则对ZK活载进行最不利荷载布置。根据M/r法，由梁轴曲率引起的等效外加扭矩为弯矩与曲线半径的比值，故活载沿纵向的布置首先应使跨中截面产生最大弯矩，才能在该处得到最大扭矩荷载及最大畸变荷载分量。ZK标准活载作用于等效直梁上的分布扭矩荷载mL(z)为

(6)

式中，1+μ为动力作用系数，根据《高速铁路设计规范》(TB 10621—2014)，对于2.1节中的算例， 1+μ=1.126；qL(z)为ZK标准活载中的均布力；Mi(z)为ZK活载中的集中力引起的相应弯矩。

(2)ZK标准活载产生的离心力。根据《铁路桥涵设计规范》(TB 10002—2017)[12]，对于高速铁路，离心力Pc(z)沿截面横向水平作用于轨顶以上1.8 m处，对截面产生的效应包括横向力和扭矩两部分，其中扭矩为mc(z)=Pc(z)eh，eh为轨顶以上1.8 m处至截面重心的垂直距离，本文按有砟桥面计算，作用点距桥面距离为轨枕高度(17.5 cm)+轨底至挡渣墙顶面高度(不少于20 cm)+挡渣墙顶面至桥面顶部高度(约30 cm)，共计67.5+180=247.5 cm，该值再加上桥面顶部至主梁重心轴的高度，即为eh的取值(对于本文算例，eh=2.9 m)。ZK活载中的均布力和集中力分别在各自的作用位置产生均布扭矩mcq(z)和集中离心扭矩mcP(z)，见式(7)

(7)

式中，v为桥梁的设计速度，根据《铁路桥涵设计规范》(TB 10002—2017)[12]，高速铁路为初期运营速度不小于200 km/h的客运专线铁路，取200 km/h；f为竖向活载折减系数，对于2.1节中的算例，f=0.696；ln为均布力加载长度。

当计算速度大于120 km/h时，ZK活载与离心力的组合考虑3种情况：

①不折减的ZK活载和按120 km/h速度计算的离心力(f=1.0)，此时mc(z)=0.945eh[PnL(zi)+qL(z)]ln；

②折减的ZK活载和按设计速度计算的离心力(f=0.696)，此时mc(z)=0.11eh[PnL(zi)+qL(z)]ln；

③没有离心力时ZK活载作用的情况。

针对研究内容，取工况b下的离心力进行计算。

(3)横向摇摆力。高速铁路横向摇摆力取80 kN[12]，作为一个集中荷载取最不利位置(本文取跨中)，以水平方向垂直线路中心线作用于钢轨顶面，由此在跨中截面产生的集中扭矩为mw=80ew，ew为轨顶至截面重心的垂直距离，为67.5 cm加上桥面顶部至主梁重心轴的高度，本文为110 cm。

以上分布扭矩均可按图2进一步分解为刚性扭转荷载和畸变荷载，其中畸变荷载分力偶为m(z)/2。

2.3 使用荷载下的畸变效应分析

针对2.1节中的算例，采用1.3节中的方法建立其弹性地基梁有限元模型，根据M/r法，将不同工况下分布扭矩m(z)的畸变分力偶m(z)/2作为竖向荷载分别施加在弹性地基梁模型上，有限元模型见图4。

图4 不同荷载在弹性地基梁上产生的畸变分力偶

当列车时速为200 km/h，曲线半径为2 000 m时，两隔板简支曲线结合梁在不同荷载下和总荷载下的畸变效应分别见图5和图6，图例中的“ZK活载”包括了其动力效应，以下同。

图5 不同荷载下24 m梁的畸变效应

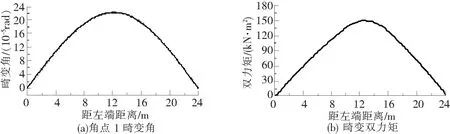
图6 总荷载下24 m梁的畸变效应

由图5、图6可知：在各种荷载中，ZK活载离心力产生的畸变效应最大，其次是横向摇摆力，二期恒载和ZK标准活载畸变效应较小。由于弹性地基梁的挠度对应于真实组合梁的畸变角，弯矩对应畸变双力矩，因此各种荷载下的截面畸变角均为抛物线形；由于横向摇摆力畸变分力偶在弹性地基梁上为集中力，故其畸变双力矩为三角形，离心力则近似为三角形，其它荷载为抛物线形。由于离心力和横向摇摆力产生的畸变效应较大，故总荷载下的畸变双力矩也表现出了近似三角形的形状。

图5中对两隔板时不同荷载的畸变效应进行了对比，下面分析4隔板和10隔板时不同荷载下畸变效应的对比，见图7。

图7 不同荷载下24 m梁的畸变效应(4隔板和10隔板)

结合图5和图7可知，不同横隔板时的畸变效应均在离心力和横向摇摆力下较大，其它荷载下较小，且隔板数越多该趋势越明显，当隔板数增大到一定数目后横向摇摆力的畸变效应更明显，这说明上述3种作用下的畸变效应出现了明显的局部效应。这是由于在弹性地基梁中，离心力的畸变力偶在跨中附近以4个等值的竖向集中荷载形式施加，而横向摇摆力的畸变力偶则为一个作用在跨中的集中荷载，由于集中效应，与集中荷载相邻的两横隔板之间畸变效应最大，较远处则很小，且隔板间距越小，这种现象越明显。

定义角点1畸变翘曲正应力与弯曲正应力的比值为畸变应力比

(8)

式中，σdω(z)为畸变翘曲正应力，即式(3)中的σ1，σdω(z)=σdω1(z)+σdω2(z)+σdω3(z)，σdω1(z) 、σdω2(z) 、σdω3(z)分别为由二期恒载、ZK标准活载(包括动力效应和离心力)和横向摇摆力产生的角点1畸变翘曲正应力。对于2.1节中的算例，角点1的畸变常数2Ω=3.811×1010N·m4，S=-3.584×1011N(畸变常数的表达式见文献 [10])。

σb(z)为弯曲正应力，σb(z)=M(z)·y/Ix。这里要注意，对于无支架施工的曲线组合梁，在施工和使用阶段承受弯曲荷载的体系不同，施工阶段的钢梁自重和混凝土湿重完全由开口槽形钢梁承担，而使用阶段荷载则由闭口组合截面承担。故弯曲正应力σb(z)=σb0(z)+σb1(z)+σb2(z)+σb3(z)，其中σb0(z)为无支架施工的组合梁在施工阶段由钢梁自重和混凝土湿重在开口槽形钢梁上产生的角点1弯曲正应力，σb1(z)、σb2(z)、σb3(z)分别为由二期恒载、ZK标准活载(考虑动力效应和离心力)和横向摇摆力在闭口组合梁上产生的角点1弯曲正应力，其中离心力和横向摇摆力均产生横向弯矩及其正应力。

根据式(3)和式(8)，可得角点1畸变正应力和畸变应力比沿梁轴的分布如图8所示。

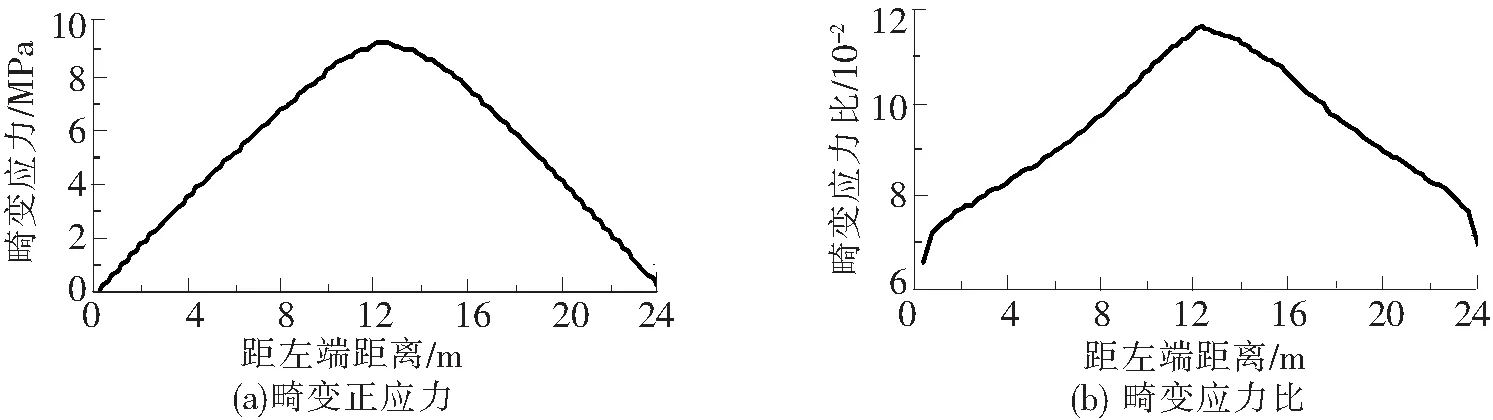
图8 总荷载下24 m梁的畸变应力和畸变应力比(2隔板)

由图8可知，只设2个端横隔板时，24 m曲线结合梁畸变正应力及畸变应力比均在跨中截面最大。由于铁路桥梁曲线半径较大，各截面畸变应力比基本均在0.12以内，只有跨中附近的部分截面畸变应力比略超过了0.1。

3 参数分析

影响曲线组合梁畸变效应的参数主要包括横隔板数量N、曲梁计算跨度l、曲线半径r，由于涉及到离心力，本文还考虑了行车速度的影响。截面几何参数(混凝土板厚、钢梁腹板高度和钢梁下翼缘宽度)对组合梁畸变效应的影响很小[13]，故此处不再研究。

3.1 横隔板对畸变效应的影响

针对2.1节中的算例，保持l=24 m，曲线半径r=2 000 m不变，变化横隔板数量N，分别考虑沿梁轴共设4、6、8、10、12块横隔板，得到总荷载下曲线结合梁畸变双力矩和角点1(图1(b))畸变角沿梁轴的分布如图9所示，图中数值均为总荷载下畸变效应的总和(以下同)。

由图9可知：

(1) 沿梁轴方向，不同横隔板时畸变双力矩和角点1畸变角均在跨中达到最大，图中的畸变效应相对跨中并不对称，是由于ZK活载并未对称布置所致。

(2) 随横隔板数目增加，各截面畸变双力矩和角点1畸变角均明显减小，且表现出近似指数函数的下降规律。以畸变双力矩最大的跨中截面为例，4隔板与2隔板相比，畸变角和畸变双力矩分别下降45.4%和88.3%；6隔板与4隔板相比，分别下降38.0%和60.7%；8隔板与6隔板相比，分别下降36.8%和24.6%，说明中横隔板的设置对减小畸变效应作用明显。但从图9(d)可以看出，随隔板数增多，跨中截面畸变角和畸变双力矩的降低幅度逐渐减小，N>8后，再增加横隔板时，减小幅度不再明显。

在目前的工程实践中，一般通过将畸变应力比控制在一定范围内来确定横隔板最大间距。美国的AASHTO规范[14]和日本的HEPC规范[15]分别将最大畸变应力比控制在10%和5%，由图9(c)可知，对于2.1节的算例，两隔板时曲线简支结合梁在使用荷载下跨中最大畸变应力比为0.116，超过了最大限值。

图9 畸变双力矩和角点1畸变角随横隔板数量的变化

3.2 曲线半径和跨度对畸变效应的影响

针对2.1节中的算例，保持跨度l=24 m，横隔板数量N=4不变，变化曲线半径，分别取r=2 000 m、2 500 m、3 000 m、3 500 m、4 000 m，可得跨中截面角点1畸变应力比如图10所示。取跨度分别为14 m、18 m、22 m、26 m、30 m，保持横隔板间距C=2 m及其它条件不变，得到跨中截面角点1畸变应力比如图11所示。

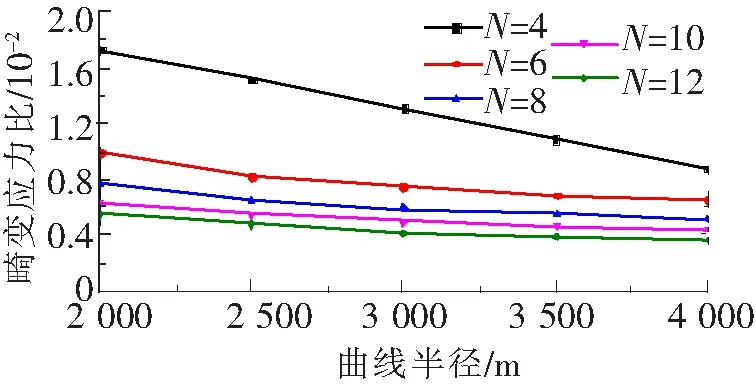
图10 畸变应力比随曲线半径的变化

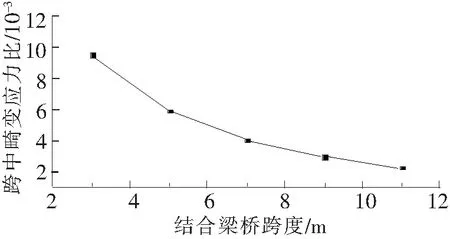
图11 畸变应力比随跨度的变化

由图10和图11可知：

(1) 随曲线半径的增大，跨中截面角点1畸变应力比逐渐减小，基本呈线性规律下降；

(2) 当横隔板间距和截面尺寸相同时，畸变应力比随跨度的增加以指数规律逐渐减小。

3.3 行车速度对畸变效应的影响

离心力的大小与行车速度有关。其它条件不变(l=24 m，N=4，r=2 000 m)，分别取行车速度为200 km/h、250 km/h、300 km/h、350 km/h，畸变应力比随行车速度的变化见图12所示。

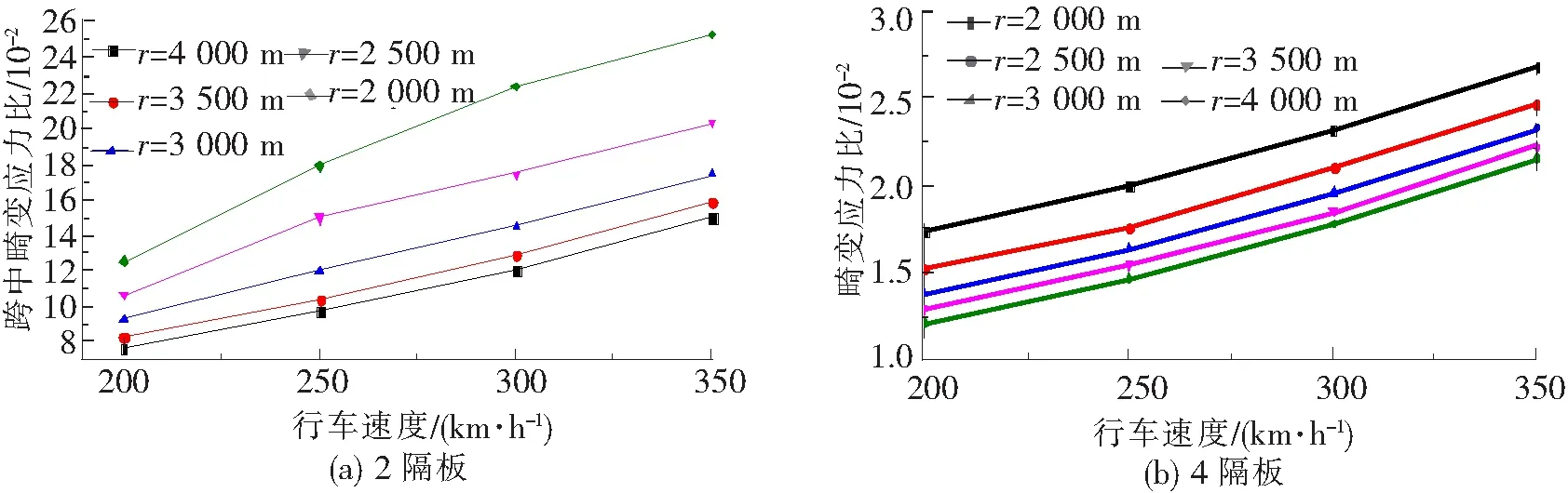
图12 畸变应力比随行车速度的变化

由图12可知，由于离心力在总畸变荷载中贡献较大，故畸变应力比随行车速度的增加呈现线性增大的趋势。只有2个端横隔板时，对于各种曲线半径，在各种高铁行车速度下跨中截面畸变应力比基本都超过了0.1，但在跨中增加2个横隔板后，基本应力比大幅减小，在目前最高运营时速350 km/h和高铁桥梁最小曲线半径下，跨中截面畸变应力比也没有超过0.1，甚至小于0.05。说明对于高铁桥梁中的单箱单室曲线结合梁，由于不存在活载偏心，只设置1到2个中横隔板即可满足控制畸变应力和畸变变形的要求。另一方面，为避免受压区钢梁的局部屈曲，可根据《铁路桥梁钢结构设计规范》(TB10091—2017)中的构造措施要求设置足够数量的加劲肋即可。