岩体结构面参数对岩石锚杆抗拔与变形影响的试验研究

(中国地质大学(武汉) 工程学院, 湖北 武汉 430074)

0 引言

岩石锚杆在岩土、采矿、边坡治理等领域具有广泛应用。 岩体内部通常会存在由于节理，裂隙等结构面而造成的岩体非连续性。岩体结构面特征包括产状、密度、连续性、张开度等参数，这些结构面参数对于岩石锚杆的力学性能影响显著，导致锚杆-灌浆材料-岩体系统在外力作用下表现出完全不同于完整连续围岩体的受力及变形特征。

国内外学者对节理岩石锚杆的研究工作大致分为试验研究和理论/数值分析两大方面。在试验研究方面，Bjurström[1]指出锚杆切向抗剪能力在保持节理岩体稳定性和限制岩体大变形方面作用非常显著。Yoshinaka et al[2]根据节理岩体锚固试验讨论了锚杆抗剪刚度与锚杆数量、弹性模量、结构面几何性质、倾角等参数的关系。张伟丽等[3]考虑了融雪期冻融循环对岩石锚杆的支护体系材料性能的影响,通过锚杆抗拔试验研究了锚杆内部应力-应变规律。刘爱卿等[4]针对施加预应力的锚杆结构面模型进行抗剪试验，发现预应力增加有利于抑制结构面变形破坏。Spang et al[5]研究了不同材料中锚杆的抗剪作用，认为岩体的变形能力是影响锚固节理岩体抗剪能力的最重要参数之一，同时将剪应力-位移曲线划分为弹性、屈服和塑性3个阶段并分别进行了讨论。丁士君等[6]在对输电线路岩石锚杆的荷载试验研究中设计了单锚，直锚式群锚以及承台式群锚模型进行荷载试验，发现岩石锚杆基础能适应强风化的岩体，同时基础的风化程度越大，其承载力越小而位移越大。Ferrero[7]对加锚混凝土及岩石进行了剪切试验，指出影响抗剪强度的因素有锚杆材质、杆体尺寸及岩石类型。Grasselli et al[8]的研究显示锚杆锚固节理岩体剪切位移达到一个临界值时，形成塑性铰，锚杆的失效主要是由于集中在两个塑性铰之间的拔力。此时锚杆抗剪力贡献值达到最大值，约为锚杆最大剪切强度的90%。

在理论分析和数值模拟方面，林杭等[9]应用FLAC3D研究全长注浆锚杆对开挖边坡支护作用效果并进行分析，根据位移云图判断潜在的滑移面，边坡的安全系数。孙长帅等[10]研究发现以往规范中单锚基础抗拔承载力计算模型中的理想角度45°破坏模式与实际经验不符，导致计算的结果不安全。Eligehausen et al[11]研究了冻融循环作用对锚杆注浆料蠕变性能的影响。Pellet et al[12]通过理论方法研究了锚杆的抗剪能力，发现垂直节理面安装的锚杆容许变形量最大，并且容许变形量随着锚杆与节理面安装角度的减小快速降低。 Benmokrane et al[13]研究了锚杆抗拔荷载-位移为指数或折线模型，其形式受模型尺寸、加载时间、围岩力学性质等因素影响。Nie et al[14]应用二维非连续变形分析方法(DDA)研究了岩体节理面对完全灌浆岩石锚杆(单锚和群锚)的受力影响特性，指出单锚产生的岩石加强单元(RRU)通常为倒锥形并受结构面走向产状控制；而群锚产生的岩石加强单元主要由结构面产状和锚杆间距影响。葛修润等[15]通过理论和试验分析，探讨了锚杆对节理面抗剪性能的影响，提出了估算加锚节理面抗剪强度和最优锚固安装角的公式。Deb et al[16]应用锚杆-灌浆界面分离模型模拟研究全长灌浆锚杆荷载传递机理。 鲁洪强等[17]基于分布式光纤传感技术监测了岩质边坡锚杆变形分布规律。刘泮兴等[18]研究了锚杆支护在整治高地应力软岩隧道大变形的效应。

基于前人研究成果，通过试验着重研究节理岩体中锚杆在轴向力作用下的受力机制和变形模式。与边坡支护及基坑支护中主要受剪切力作用下的锚杆不同，轴向受力的岩石锚杆常见于预应力设备基础，如风力发电机基础中。这类岩石锚杆是基础结构中的主要受力构件，岩石节理裂隙等结构面对锚杆的承载性能将会产生显著影响。通过室内模型试验研究复杂地质条件下不同结构面参数对锚杆的抗拔性能以及围岩体的受力破坏形式。期望为在节理岩体中主要承受轴向力(如预应力)的岩石锚杆结构的设计提供试验依据。

1 试验概况

锚杆轴向锚固力试验以抗拔试验为主，为研究锚杆在岩体结构面存在下的抗拔性能以及破坏形式的探究性室内模型试验，在总结了前人在结构面特征对岩体力学性质影响方面的研究基础上，选定结构面迹长(连续性)，结构面倾角(产状)以及结构面数量(密度)3个主要影响因素进行探讨。为定量研究岩体结构面的规律性并考虑试验条件，试验采用混凝土试件代替天然岩块。按表1组合分别在边长为20 cm的立方体混凝土设置不同边长，不同倾角以及不同数量的3类结构面模型以确保试验的代表性，相同结构面尺寸的模型分别制作两组共12块。

表1 模型试验结构面设置参数

注：共两组12个试块。试块编号：第一组为1-1到1-6，第二组为2-1到2-6。

试验混凝土采用42.5 MPa普通硅酸盐水泥，水灰比0.41、碎石粒径10～30、中粗砂，按C40标号混凝土进行配比，每立方米混凝土所需的原材料：水泥482 kg、中粗砂0.45 m3、碎石0.79 m3、水200 kg；水灰比0.41。混凝土立方块体中设置如表1所示不同类型的结构面并预埋插入锚杆，锚杆材料为直径16 mm的HRB335钢筋；需要指出的是由于试件尺寸等条件限制，锚杆直接预埋在混凝土试件中，未设置砂浆界面层。按照设计倾角和迹长在混凝土试件中预埋2 mm厚PVC发泡雪弗板形成并模拟岩体中的结构面。相较于普通泡沫材料，PVC发泡板常用于建筑模型制作，便于切割成型，切割后边角完整碎屑少。由于其采用PVC材料进行发泡，其密度与强度都比较大，在模型中能很好地保持结构面的原有形态，不易变形。在混凝土浇筑到一定高度后将固定有结构面的锚杆垂直插入模型的正中央，测量结构面角度，分层浇筑混凝土，同时注意固定结构面位置，使之保持倾角与锚杆的相对位置。为研究混凝土内部锚杆应力-应变的变化规律，在锚杆距混凝土上表面5 cm，10 cm，15 cm处设置3个应变片，应变片的标准电阻为120 Ω。图1为预埋PVC发泡板形成的结构面及试件尺寸和应变片位置。

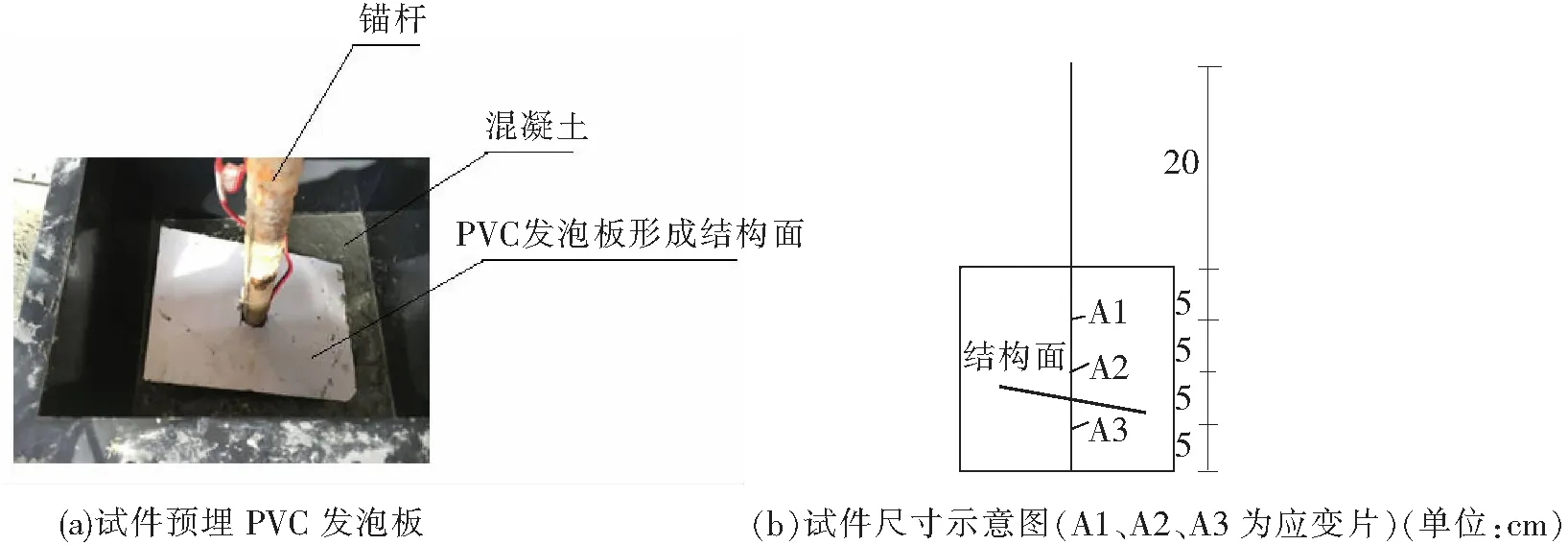
图1 结构面和试件尺寸

选取不同结构面特征：产状，密度，连续性三类特征进行试验，图2为试验中结构面不同迹长，倾角以及数量在锚杆轴向方向的示意图。其中L为结构面迹长，α为结构面和竖直方向倾角，H为结构面在竖直方向投影长度。

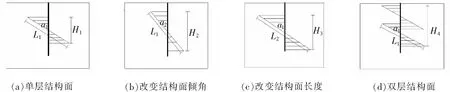
图2 不同迹长，倾角以及数量的结构面在锚杆轴向分量示意图

以上模型试件均在标准养护环境下养护28 d，与模型试件同时制作6个70.7 mm立方体抗压试块用来检验混凝土强度，抗压试块和试验模型试件在相同条件下养护。在14 d(1-3号试块)和28 d(4-6号试块)对试块进行轴心抗压试验，试验采用YAW-300D型全自动压力试验机进行逐级加载。经过28 d养护后的试块强度达到了C40混凝土强度的97%以上，表明试验模型混凝土强度符合C40标号。

在试件进行28 d标准养护后，采用UTM600kN万能材料试验机进行锚杆的拉拔试验，由于试验机采用夹头与样品相连，考虑到混凝土抗拔模型的特殊性不能直接与试验机夹具相连，故将抗拔块体倒置放入特制的拉拔支架当中，支架上部与试验机的上部夹具相连，抗拔模型倒置放入支架内，伸出的钢筋与下部夹头相接。支架上下两侧均有可活动的对中仪，能够使试验中施加的拔力竖直施加仪减小误差。试验机装有新型电气控制系统，具有全数字闭环控制、多通道采集等功能的精密仪器。采用不同的夹具，能完成各种材料在拉伸、压缩、弯曲、剪切、剥离、撕裂等状态下的力学性能试验；采用微机控制全试验过程，实时动态显示力值、位移值、变形值、试验速度和试验曲线；采用微机进行数据处理分析，试验结果可自动保存。应变片数据通过优泰静态应变仪接收处理。

2 试验结果分析

试验锚杆为直径16 mm的HRB335钢筋，拔力加载过程未超过锚杆屈服强度。抗拔试验出现了两种破坏形式：①锚杆与混凝土界面破坏从而导致锚杆从上部拔出，锚杆所在的顶部混凝土呈环形破坏，试件不出现裂缝；②由于模型内部存在结构面，产生了一条与结构面垂直，并且贯穿整个模型的裂缝，而锚杆所在的顶部混凝土所受破坏较小，可以判断此时为脆性破坏。

图3 锚杆弹性软化及滑移开裂阶段示意图[19]

此两种破坏形式文献也有论述：如图3，刘波等[19]建立了描述锚杆与周围介质在受拉过程中弹性状态、塑性软化和滑移开裂3个过程的数学模型。并指出锚杆处于弹性阶段时有效锚固长度为一定值，拔力超过弹性阶段后，有效锚固长度增加，轴力向深处传递，同时上部出现塑性变形进入软化阶段并伴随着变形的增加。当拔力上升超过极限荷载后软化变形进一步发展为滑移开裂破坏。朱焕春等[20]指出，螺纹锚杆在受到轴向拔力的过程中，锚杆在剪切作用下，因材料的剪切膨胀作用而产生作用于周围介质法向剪胀变形，使得周围介质的法向方向处于受压状态而产生环向破坏。该理论指出锚杆受拉时，周围介质先产生水平横向破坏，继而是孔壁的剪切破坏，使锚固体应力向深部传递。荷载的增高或荷载循环作用次数的增加都可以导致这一过程的继续；直至某一稳定深度或全部破坏。

此次试验过程采取位移程控方式进行加载，加载速度为2 mm/min。通过位移加载，能完整地反映出模型在抗拔试验中应力与应变的关系。当锚杆所受的抗拔力达到极限抗拔承载力后位移继续增大时，锚杆所受应力骤降，此时可以判断模型破坏，试验机同时会显示最大拔力值，在此基础上再进行一定位移的加载，以研究破坏后加载曲线，待其拔力基本稳定后，试验结束。

图4分别为两组单层结构面下不同迹长模型的拔力-位移图：无结构面、结构面迹长L=6 cm和L=12 cm。试验结果显示在抗拔前期拔力与位移较小时，模型整体处于弹性阶段，锚杆与混凝土共同产生弹性变形，拔力与位移接近于线性变化。当拔力达到35 kN左右时，拔力逐渐超过模型的弹性极限荷载，曲线斜率开始变缓，此时模型进入第二个阶段，即在弹性变形的基础上模型开始屈服产生塑性变形，从而进入塑性软化阶段。软化阶段进一步发展，曲线缓慢上升，随着位移的增加，拔力达到最大极限承载力后模型滑移开裂，拔力迅速下降，轴力传递到锚杆底部达到残余强度稳定值。由于存在结构面的影响，模型的完整性及整体力学性能会有一定的降低，当结构面规模即迹长增大时，模型进入塑性屈服阶段的拔力值降低。结构面迹长越大的模型会越早达到极限承载力，并且极限承载力也越低，其拔力下降的速度也越快，残余强度越低。以至于第二组L=6 cm的模型在出现滑裂后混凝土直接破坏，导致残余强度几乎为0。试验中迹长L=6 cm结构面试件最大抗拔承载大于迹长L=12 cm试件；但是试验过程中发生整体脆性破坏，裂缝贯穿整个模型，因此其残余轴力较L=12 cm结构面为低。

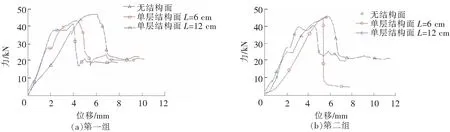
图4 单层结构面迹长模型拔力-位移图

图5为固定结构面迹长L=6 cm时，结构面数量分别为无结构面、单层、双层结构面的拔力-位移图。当结构面数量增加时，模型的完整性及整体力学性能逐渐降低。结构面数量增加，模型进入塑性屈服阶段的极限拔力值降低，结构面数量越多的模型越早达到极限承载力并且极限承载力也越低，第一组中无结构面模型极限承载力为46.1 kN，单层结构面的模型极限承载力为44.6 kN，双层结构面的模型极限承载力则大幅度降低到36.8 kN。同时结构面数量越多，模型残余强度也越低。此外，在拔力值达到极限承载力并下降后，无结构面模型开裂滑移阶段曲线平稳接近于水平。单层结构面模型在波谷最低点后，拔力值随着位移增加而增大，上升到某一极大值后下降并稳定，而存在双层结构面模型出现2次极大值。其原因是无结构面模型在滑移开裂阶段的破坏变形稳定产生，有效锚固段稳定向底部延伸。而存在结构面的模型由于结构面所处区域其力学性质远低于围岩体，所以刚开始进入滑移开裂阶段时，其破坏变形会大幅度的增加，荷载急剧度降低，轴力以及有效锚固段来不及向深处延伸，只有等到新的有效锚固段开始工作后荷载开始上升，存在双层结构面的模型也因此存在2个承载力波峰。

图5 不同结构面数量模型抗拔拔力-位移图

图6为固定结构面迹长L=12 cm，结构面倾角分别为10°、20°、30°时的拔力-位移图。当结构面倾角从10°增加到20°时，模型的极限抗拔承载力与残余强度会有所降低但不显著。当结构面的倾角从20°增加到30°时，极限承载力与残余强度会有明显的下降趋势。综上可总结原因为，结构面倾角增大时，同样大小的结构面在锚杆上的投影长度也会上升，其到锚杆的法向距离也会越短，越容易受到锚杆带来的法向破坏，模型的不完整程度与其角度的正弦函数呈正相关，所以受锚杆当角度越大时，其上升的趋势越明显。

图6 不同倾角的结构面抗拔模型拔力-位移图

表2总结了以上两组测得锚杆抗拔极限承载力数据如下。

(1)单层结构面下，在结构面倾角固定时，锚杆抗拔极限承载力随结构面迹长的增加而降低；在结构面迹长固定时，锚杆抗拔极限承载力随结构面倾角的增加而降低。

(2)多层结构面下，锚杆抗拔极限承载力随结构面数量的增加而降低。

表2 锚杆抗拔极限承载力 kN

总结以上试验数据见表3,结构面各参数对于锚杆极限抗拔承载力的影响，在单层结构面时，当模型结构面迹长从0(无结构面)分别增加到6 cm以及12 cm时锚杆最大抗拔承载力分别下降约8%和12%；当结构面的倾角从10°上升到20°及30°时，锚杆的最大抗拔承载力分别较无结构面情况下降约3%、10%和16%。当模型结构面数量从无结构面增加到单层和双层结构面时，锚杆的抗拔承载力分别下降约8%和21%。由表3可见结构面数量对锚杆抗拔承载力的影响较其它参数(迹长和倾角)更为显著。

表3 锚杆极限抗拔承载力/无结构面锚杆极限承载力

注：迹长: 1-无结构面;2-L=6 cm;3-L=12 cm(倾角固定为20°);倾角: 1-10°;2-20°;3-30°(迹长固定为12 cm);数量：1-无结构面；2- 单层；3-双层。

为研究结构面下锚杆的受力和变形，在抗拔试验中锚杆表面贴加应变片，通过优泰静态应变仪记录在抗拔试验施模型位移稳定增加(试验机采取位移加载方式，速度2 mm/min)，应变片所处位置的钢筋应变变化，通过换算公式得到锚杆的轴力以分析锚杆内部轴力的变化。选取图7(a)单层迹长L=12 cm，倾角=10°结构面模型；以及图7(b)双层迹长L=6 cm，倾角=20°结构面模型的2个具有代表性的数据分析。模型应变片及结构面位置如图7所示。

图8为迹长L=12 cm，倾角10°结构面模型的位移与锚杆轴力图。由于应变片A2未有效收集到数据，故只显示A1和A3两个界面的应变数据。从图可知，A1段锚杆轴力持续增加直到在位移4.2 mm处达到轴力最大值，说明模型在此时达到其极限抗拔承载力，这也与图8相互吻合。但应变片A3处的轴力明显小于A1，随着深度的增加，锚杆的轴力随之衰减。4.2 mm后A1处轴力迅速下降，说明此时A1和A2间的结构面所在区域滑裂位移已经产生，此后锚杆轴力稳定，滑裂破坏呈发展趋势。而A3处的轴力达到最大值后保持稳定却并未发生明显的下降趋势，原因是A3深度大于结构面所处位置，上部产生破坏尚未发展到A3处，使得A3处轴力在结构面破坏后保持稳定。

图7 模型结构面及应变片位置示意图(单位：cm)

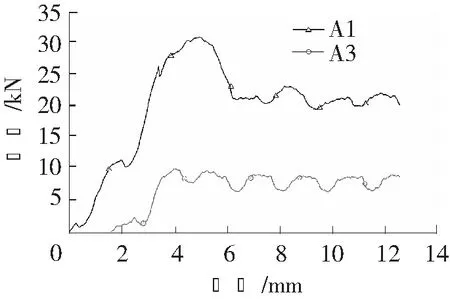
图8 锚杆轴力-位移图 (迹长L=12 cm，倾角=10°结构面模型)

图9 锚杆轴力-位移图 (双层结构面，迹长L=6 cm，倾角=20°模型)

图9为双层结构面模型，其迹长L=6 cm，倾角=20°的锚杆轴力-位移图。此图包含了A1,A2，A3应变片处轴力数据。A1段锚杆轴力随着位移加载一直增加并在位移约4.0 mm处达到最大值，说明模型在此时达到了极限抗拔承载力，随后A1轴力迅速下降，说明第一个结构面附近开始破坏轴力进一步向深处传递，A1，A2处的轴力上升。当位移加载到6 mm处时，A2轴力也迅速下降，此刻第二个结构面破坏，位移进一步发展轴力向下延伸，A2轴力在8 mm处出现小范围上升，随后一定范围内稳定。此轴力变化与图8中的双层结构面结果基本吻合。A3处的轴力在6 mm附近达到最大值后基本稳定，由于A3深度大于结构面所处位置，所以结构面破坏后的影响并未立刻传递到A3。由此可知锚杆受拉时，存在多个结构面的区域容易破坏，并且破坏区域是一个由上到下逐渐发展的过程。

3 结论与讨论

在含有结构面岩石锚杆的抗拔试验中，模型的主要破坏形式为锚杆的滑移破坏与围岩体自身破坏。抗拔模型初期处于弹性阶段，锚杆与混凝土共同产生弹性变形，其拔力与位移曲线接近于直线变化。当拔力逐渐超过极限弹性荷载，曲线的斜率开始变缓，此时模型进入第二个阶段，即在弹性变形的基础上开始屈服并产生塑性变形，从而进入塑性软化阶段。软化阶段进一步发展，曲线缓慢上升，随着位移的增加拔力达到最大极限承载力后模型滑移开裂，拔力迅速下降，轴力传递到锚杆底部达到残余强度后滑裂变形稳定产生。

试验结果显示，在单层结构面时，当模型结构面迹长从0(无结构面)分别增加到6 cm以及12 cm时锚杆最大抗拔承载力分别下降约8%和12%；当结构面的倾角从10°上升到20°及30°时，锚杆的最大抗拔承载力分别下降约3%、10%和16%。当模型结构面数量从无结构面增加到单层和双层结构面时，锚杆的抗拔承载力分别下降约8%和21%。可见当结构面的规模(迹长)，数量以及倾角增加时，都会导致结构面范围增加，使得模型不完整程度上升，模型提前进入塑性软化阶段，锚杆的极限抗拔承载力以及残余强度因此不同程度下降。结构面数量对锚杆抗拔承载力的影响较其它参数(迹长和倾角)更为显著。

当锚杆达到极限抗拔承载力产生滑裂变形破坏拔力降到极小值后，拔力值随位移增加而增大，在一定范围内上升到极值后下降并稳定；而当存在两组结构面模型会出现两次极值。原因是在无结构面模型在滑移开裂阶段的破坏变形稳定产生，有效锚固段稳定向底部延伸。而存在结构面的模型由于结构面所处区域其力学性质远低于围岩体，所以刚开始进入滑移开裂阶段时，其破坏变形会大幅度的增加，荷载急剧度降低，轴力以及有效锚固段来不及向深处伸，只有等到新的有效锚固段开始工作后荷载开始上升。存在两层结构面的模型也因此存在两个波峰。

在抗拔试验的模拟结果中当锚杆受到上拔力作用时，模型顶部锚杆所在的区域首先发生塑性变形，随着拔力的增加，塑性区以锚杆为中心，向四周拓展，锚杆内的拔力向模型深处传递，塑性区域也逐渐向下部发展，塑性变形区域呈倒锥形，贯通整个模型。当增加结构面的面积，倾角以及数量时，均会加速结构面所在区域塑性变形的发展使模型更易破坏，其中结构面的数量是模型破坏的最不利因素，当结构面数量增加时，会在多条结构面之间形成一条塑性变形软弱带，其发展迅速使模型完整性进一步降低，整体抗拔性能大幅度下降。结构面的参数控制着模型塑性变形的发展。模型在受拉过程中，会在顶部形成一个椭圆形的塑性区域，该区域的长轴方向受结构面控制，与结构面的倾向方向一致。在模型内部沿结构面倾向方向，结构面所在区域会比邻近区域率先发生塑性变形，其范围也比邻近区域要大，沿着结构面所在的范围分布。模型内部的塑性区会沿着结构面的倾向和走向两个方向发展，其中沿走向方向的塑性区大致以锚杆所在区域为中心呈对称分布。并且走向方向的塑性区发展速度要大于倾向方向，率先抵达模型边界，使得模型整体发生破坏。

以上结论仅基于本次试验，讨论如下。

(1) 试验采用PVC发泡板预埋于混凝土试件模拟岩石体结构面，由于试验条件及模型尺寸等因素制约，锚杆预埋于混凝土试件中，锚杆周围忽略灌浆层。考虑主要研究结构面对锚杆的抗拔影响。如后期试验考虑灌浆层，由于灌浆层强度一般高于混凝土强度，从而增加了锚杆外界面的握裹力，从而使得本文试验结果偏于保守。

(2) 试验中结构面为规则平面，且双层结构面平行设置。实际岩体结构面的几何形状和结构面之间相对位置错综复杂。本文仅对最简单的单双层结构面进行了模拟研究。后续研究应考虑拓展更有一般代表性的模型结构面设置。

(3) 本文考虑了结构面迹长对锚杆抗拔承载力及变形的影响，这是基于结构面面积和迹长成正比情况下的假设进行探讨。实际岩体结构面为二维平面或三维曲面，考虑结构面实际面积的影响更为合理，应在后续研究完善。

(4) 本次试验着重研究了单根锚杆在结构面岩体中的抗拔性能，针对群锚的研究应在后续课题中完成。