基于模态分解的下位玻璃关门异响试验分析*

高云凯, 石 旺， 杨肇通， 王跟海

(同济大学汽车学院 上海，201804)

引 言

汽车车门是汽车整车上一项重要的结构件与最常使用的开闭总成，车门不但影响汽车的碰撞安全性、空气动力特性及密封性，其关门振动噪声特性也是消费者判断整车品质的主要内容之一。自20世纪80年代以来，汽车车门关闭的振动噪声问题越来越受到重视[1]。通用汽车公司对汽车振动噪声仿真预测进行了一定程度的研究，工程人员探究了有限元法在乘客舱声腔模态中的应用，探讨了乘客舱声场对汽车结构振动的影响，建立了汽车结构声学混合有限元分析模型[2]。目前，国外对于关门振动噪声设计已经上升到声品质高度，提出了响度、尖锐度、粗糙度以及二次冲击等心理声学客观参数[3-5]。近些年来，国内学者通过不同方法来分析和治理车门关门振动噪声源，关门声品质的评价分析逐渐成为研究热点[6-10]。

工作变形(operational deflection shapes，简称ODS)分析是一种新型的机械结构振动分析方法，它不同于传统的机械结构模态分析。模态频率及振型是机械结构的一种固有特性，工作变形则是指在一定的工况下，对于特定的测量及激励频率范围，各个节点测量自由度之间的主要振动响应形式。对于机械结构而言，模态均有其特定的振动频率，而工作变形根据激励和工况的不同，可能出现在多个不同的频率处[10-12]。工作变形试验中的模态分解是将每一个工作变形分解为模态振型的线性叠加，根据各个模态的参与因子判定主要振动辐射噪声源。

笔者以某车型为例，该车型车门在长期使用后产生了较为严重的异响声。通过工程反馈，在使用过程中车门外板、车门铰链、车门锁等线性元件未产生较大变化，因此车门异响现象并非是由车门外板等线性元件直接造成的。对下位玻璃状态下的车门进行半约束模态试验和关门工作变形试验，获得车门模态频率振型、工作变形振动数据以及关门噪声信号。对关门噪声信号进行短时傅里叶变换时频分析，并与对标车噪声信号时频图进行对比分析，判定出关门声存在二次冲击现象，且噪声能量主要分布在低频段。对工作变形振动数据进行分析，获得主要工作变形频率及振型，通过模态分解分析，得到主要参与模态振型，识别出车门异响主要振动噪声源，指出改进方向。改进试验结果显示，改进后此车门异响消失，时频分析中二次冲击现象消除。

1 车门工作变形试验

1.1 工作变形试验原理

工作变形试验反映的是在工作状态下，对于特定的激励频率，工作系统以工作振动的方式表现出各个测量自由度之间的相对加速度幅值关系[13-14]。利用位移-力的频响函数{H}为基础的模态振型，用{X}代表工作变形，可表述为

(1)

其中：i为测量自由度的序号；ωp为特定的角频率；Fj(ωp)为自由度j激振力(输入)的线性谱；m为激振力数目；Vik,Vjk为多个模态振型中的第i列和第j列向量。

尽管系统的固有频率一定，但是系统受到的激励往往并非和固有频率存在一致关系。因此，系统对于特定测量频率的响应往往是若干个模态频率振型的线性叠加。具体的，若工作变形的某个频率响应趋近于0，则该阶模态贡献极小；若测量频率接近模态频率，则该阶模态往往是工作变形的主要贡献模态。对于其他测量频率响应较高的工作变形，可能是若干个模态相互叠加耦合的结果。

工作变形的模态分解一般在频域内进行，以试验结构敏感位置的一个测点作为参考点，采集其余测点的振动信号，根据功率谱计算测点相对于参考点的频率响应函数(frequency response function，简称FRF)

(2)

其中：Gii(ω)为系统的自功率谱密度函数(测点i)；Gjj(ω)为系统的自功率谱密度函数(参考点j)；Gij(ω)为系统的互功率谱密度函数(测点i-参考点j)。

此ODS频率响应函数包含了选定测点的幅值数据以及测点i相对参考点j的相位信息。

1.2 工作变形模态分解原理

根据模态叠加原理，工作变形可根据式(3)分解为结构固有模态振型的线性叠加

(3)

其中：Xi(ω0)为在工作频率ω0处的工作变形向量；Vk为模态k的振型向量；ak为模态k的叠加比例系数；Rest为相对误差。

根据式(3)可以得到工作变形的主要参与模态振型，从而识别出主要参与模态和主要振动噪声源，并进行针对性改进。

1.3 工作变形试验方法

1.3.1 试验对象及测试系统

本次试验对象为某车型左前车门，试验在整备车上进行。测试系统主要包括传感器、数据采集与记录系统及工况控制装置。传声器为B&K公司生产的内置ICP全指向传声器，加速度传感器为PCB公司制造的结构测试ICP三向加速度传感器。采用LMS公司LMS SCADAS Ⅲ SC316-UTP数据采集系统和LMS.Test.Lab试验数据处理分析系统，采用关门速度计和橡皮绳蓄能装置控制关门速度。

1.3.2 传感器测点布置

汽车车门由众多零部件组成，且车门内外板面积较大，因此测点布置应符合正确反映车门变形的原则。加速度测点偏少则较难反映被测车门的结构基本特征和主要零部件的振动特性，使工作变形振型很难正确反映出来；加速度测点偏多则会增加工作量及试验数据处理分析的复杂程度。因此，加速度测点布置主要有以下原则：

1) 总体上能反映关键部件的关键振动特征；

2) 测点应尽量避开振动节点，否则会丢失主要变形；

3) 在试验中主要关注的部位，测点布置应该较密集一些，对于规则的部件尽量采取对称布置。

在关门过程中车门所受到的激励主要来自于锁销，因此应在车身锁销处布置1个三向加速度传感器，用来测量激励信号。

结合上述原则，具体布置如表1和图1所示。

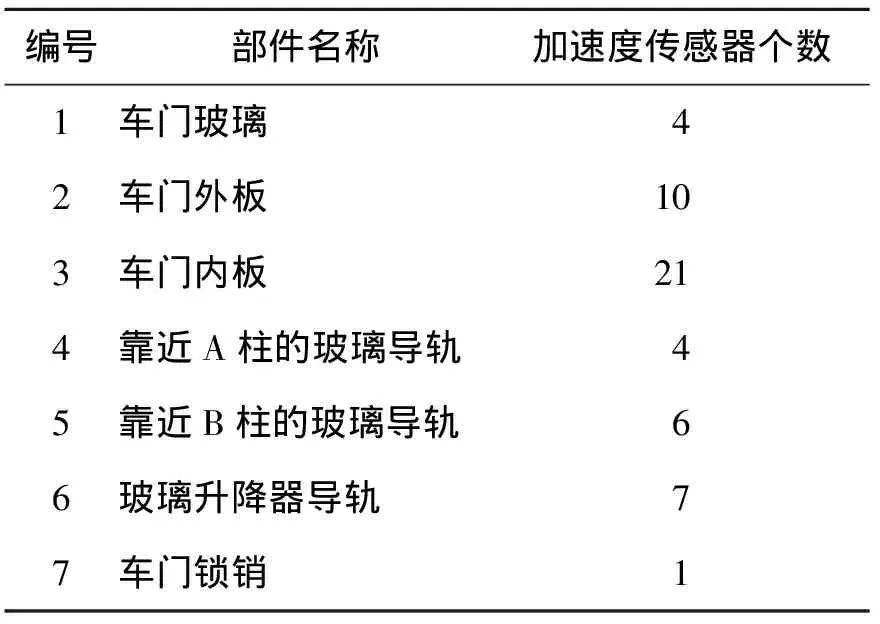
表1 整备车门工作变形试验加速度传感器布置

图1 工作变形试验传感器布置图Fig.1 The arrangement of accelerometer on door

本次试验共2个传声器，分别布置于车内驾驶员右耳位置、车外开门处用户右耳位置，采集这两处位置声压信号。传声器位置及编号名称如表2所示。

表2 传声器编号及位置描述

1.3.3 工作变形关门工况设置

由于在玻璃下位状态下车门异响较为严重，因此设定整车左前门玻璃处在下位状态，其他车门玻璃处在上位状态。在车门锁销附近安装速度计测定关门速度，利用橡皮绳蓄能装置使关门速度稳定且具有可重复性。根据工程经验，正常的最小关门速度一般在0.8～1.5m/s之间，本次试验关门速度设定为1.0m/s。

图2 关门速度计及橡皮绳关门装置Fig.2 The speedometer and rope device

1.4 关门噪声分析

汽车关门噪声信号具有典型的非稳态特征，传统的傅里叶变换方法难以获得非稳态信号的完整而准确的时频信息。短时傅里叶变换(short time Fourier transform，简称STFT)则具有分析信号在任意局部范围内时频特征的能力，其定义可表述为

信号x(t)在时间τ的短时傅里叶变换即为信号x(t)乘上一个以t=τ为中心的分析窗ω*(t-τ)所做的傅里叶变换。由于乘上一个相当短的窗ω*(t-τ)，等价于取出信号在t=τ附近的一个切片，因此STFT具有反映一个信号在任意局部范围频率特性的能力。

采用STFT的数据处理方法，获得关门噪声信号的时频特征，选取车外开门处用户右耳处传声器所测得的声压信号，利用STFT绘制出声压级时频图，如图3、图4所示。

图3 车外测点S2声压级时频图Fig.3 The time-frequency analysis of sound

图4 对标车测点S2声压级时频图Fig.4 The time-frequency analysis of marked car sound

车外开门处用户右耳处声压信号时频图表明关门声存在二次冲击现象，且二次冲击的时间间隔为0.023s。根据图中颜色变化判断出噪声能量主要分布在低频段，而车门部件所产生的振动辐射噪声为低频噪声。因此，抑制车门在关门过程中的工作变形振动，尤其是与二次冲击时间间隔相关的工作变形能有效地降低关门噪声。

1.5 工作变形试验分析

以车身锁销处的加速度测点为参考点，获取各测点相对于参考点的ODS频率响应函数，并对频率响应函数进行汇总，进行工作变形处理分析，如图5所示。在主要频率频段内选取工作变形响应曲线的主要峰值频率，得到主要工作变形频率及其振型。

图5 车门工作变形响应曲线及峰值频率Fig.5 Response curve and peak frequency of ODS

根据图5中获取的工作变形峰值频率，得到各个峰值频率下的整备车门工作变形振型，对其进行描述汇总，如表3所示。

表3 车门主要工作变形频率及变形描述

对车外测点S2声压级时频特征的低频部分进行分析，认定各主要频率下的工作变形频率均在声学响应中存在明确的对应关系，表明工作变形主要频率选取有效，如图6、图7所示。

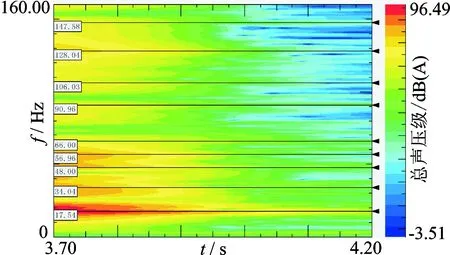
图6 车外测点S2声压级低频部分时频图Fig.6 Low frequency section of time-frequency result

图7 车门前4阶工作变形振型Fig.7 The shapes of vehicle door ODS

结合图5、图7和表3进行分析可得：

1) 车门工作变形中，100Hz以下低频部分振动剧烈，抑制低频工作变形振动能够有效地降低车门振动辐射噪声；

2) 在前4阶工作变形振型中，靠近A柱的玻璃导轨与下位状态下的车门玻璃均有较为剧烈的振动，表明此玻璃导轨在关门过程中容易与玻璃振动产生较大的低频振动辐射噪声；

3) 第3阶工作变形频率为44.50Hz，与二次冲击的时间间隔0.023s存在倒数关系。此阶工作变形以玻璃导轨与车门下位玻璃的俯仰变形为主。改进或增强车门玻璃及导轨的约束能够抑制玻璃及其导轨振动，改善二次冲击现象；

4) 在各阶工作变形振型中，车门门窗框上缘与车门后上角振动均较为明显，改进此处刚度对关门工作变形有较好的改善作用。

2 整备车门半约束模态试验

2.1 试验测试系统

测试系统主要由3部分组成：激振与测量系统、数据采集系统以及模态处理分析系统。

激振系统主要为力锤，采用PCB公司制造的Modally Tuned ICP冲击力锤作为激振器。

测量系统、数据采集系统均与工作变形试验相同，模态处理分析系统则采用LMS.Test.Lab中的Impact Testing 模块。

2.2 整备车门约束方法

整备车门在关门瞬间处于半约束状态，车门受到车门铰链与限位器的约束，除绕z轴的转动自由度外，其余5个自由度均被约束。汽车白车身模态试验所采用的汽车车身在使用过程中一般通过悬架与轮胎支撑在地面上，悬架与轮胎可视为弹簧系统，因此白车身一般采用弹簧支撑或自由悬挂方式进行自由模态试验。汽车车门作为开闭件通过铰链约束在车身上，开闭过程中仅存在绕z轴的转动自由度，因此半约束模态试验相比于自由模态试验更加能反映车门在关闭瞬间的物理状态。

在车门两侧远端非结构位置布置橡皮绳，使车门绕z轴方向处于自由转动状态。整备车门系统的约束如图8所示。橡皮筋约束装置应保证系统的刚体模态频率低于结构自身第1阶弹性模态频率的10%～20%[15-16]。对橡皮筋的弹性系数进行测量，经分析后计算出刚体模态为0.6Hz，约为1阶模态的3.8%。

图8 整备车门系统半约束状态Fig.8 The semi constrained state of door

2.3 模态试验传感器布置

整备车门工作变形分析中需进行模态分解，识别模态参与因子，因此车门模态试验中的加速度传感器布置与工作变形试验相同。同时由于不需要测量车门锁销处的加速度激励，因此撤去车门锁销处的三向加速度传感器。

2.4 模态试验结果

基于模态处理分析系统，对采集的数据首先在主要研究频段内(0～240Hz)进行相干性检查，测点加速度与力锤激励力的相关性在0.8以上，说明各测点的响应与激励相关性较好，激励有效。汇总各个测点的FRF函数，利用PolyMAX模块进行模态参数辨识。车门模态参数辨识结果如表4所示，图9为车门前4阶模态振型图。

表4 车门模态频率及振型描述

图9 车门前4阶模态振型Fig.9 The first fourth modal shapes of door

2.5 模态有效性验证

模态判定准则(modal assurance criteria，简称MAC)是验证各阶模态频率是否有效的一种可靠数学工具。假设两个描述物理模态的向量分别为X和Y，则其判定准则MAC可表示为

(5)

其中：W为加权矩阵，通常取单位矩阵。

由式(4)可知，如果X，Y是描述同一物理模态的两个向量，则MAC=1；如果两个向量描述的是不同的物理模态，则MAC=0。利用此模态判定准则对辨识出的车门模态进行模态有效性验证，得到如图10所示的模态置信图，图中任何两个不同模态间的MAC值均小于20%，表明试验中识别出的车门模态具有良好的模态纯度。

图10 车门模态置信图Fig.10 The MAC of vehicle door modal

2.6 模态结果分析

由表4及图9可看出：

1) 车门前2阶模态振型均为车门整体振动，此模态频率及振型与车门铰链安装处的刚度特性有关；

2) 车门第3阶模态为玻璃绕z轴横摆局部模态，且靠近A柱的玻璃导轨因玻璃绕z轴横摆而产生较大的变形，对玻璃约束方式及靠近A柱的玻璃导轨的连接方式应进行改进或增强；

3) 车门第6、第7阶模态中均存在下位玻璃局部模态，且此两阶模态频率较为接近，此低频振动在关门过程中会引起较强的振动辐射噪声；

4) 车门第9、第10阶模态均为门窗框局部模态，表明需要对此处进行刚度或阻尼改进，从而抑制振动。

5) 第17阶模态为A柱玻璃导轨弯曲模态，此玻璃导轨振动易引起下位玻璃的振动。

2.7 模态参与因子识别

提取表3中各峰值频率下的工作变形，结合整备车门半约束模态试验结果，根据式(3)计算出车门固有模态对工作变形的参与因子，如表5所示。

对各主要峰值频率下的工作变形进行分析，根据图11可得出：

1) 第1阶17 Hz频率下的工作变形中参与程度较高的模态为第1阶、第5阶和第9阶，主要是车门的弯曲模态复合玻璃导轨弯曲模态叠加形成；

表5 车门工作变形模态分解表

2) 30.5Hz频率下的工作变形几乎完全由第1阶、第4～7阶、第9阶以及第16阶的模态复合而成，此频率下的工作变形主要表现为车门内外板的局部振型，贡献度较高的模态形式主要为车门的弯曲与玻璃及其玻璃升降器导轨的局部模态；

3) 第3阶工作变形频率为44.50Hz，参与程度较高的模态为第1阶、第3阶和第7阶，此阶工作变形主要是由车门玻璃的模态复合而成，可通过改善车窗水切、玻璃导轨密封条等非线性元件的刚度或压缩量来抑制车门玻璃模态及此阶工作变形；

4) 车门玻璃的模态对100Hz以下的各主要工作变形明显具有不同程度的贡献，且靠近A柱的玻璃导轨存在支撑不足，该导轨出现了多阶沿x轴的弯曲模态；

5) 导轨作为玻璃的约束边界，与玻璃的随动明显，靠近A柱的玻璃导轨未起到足够的约束作用，导致关门过程中车门玻璃振动明显。

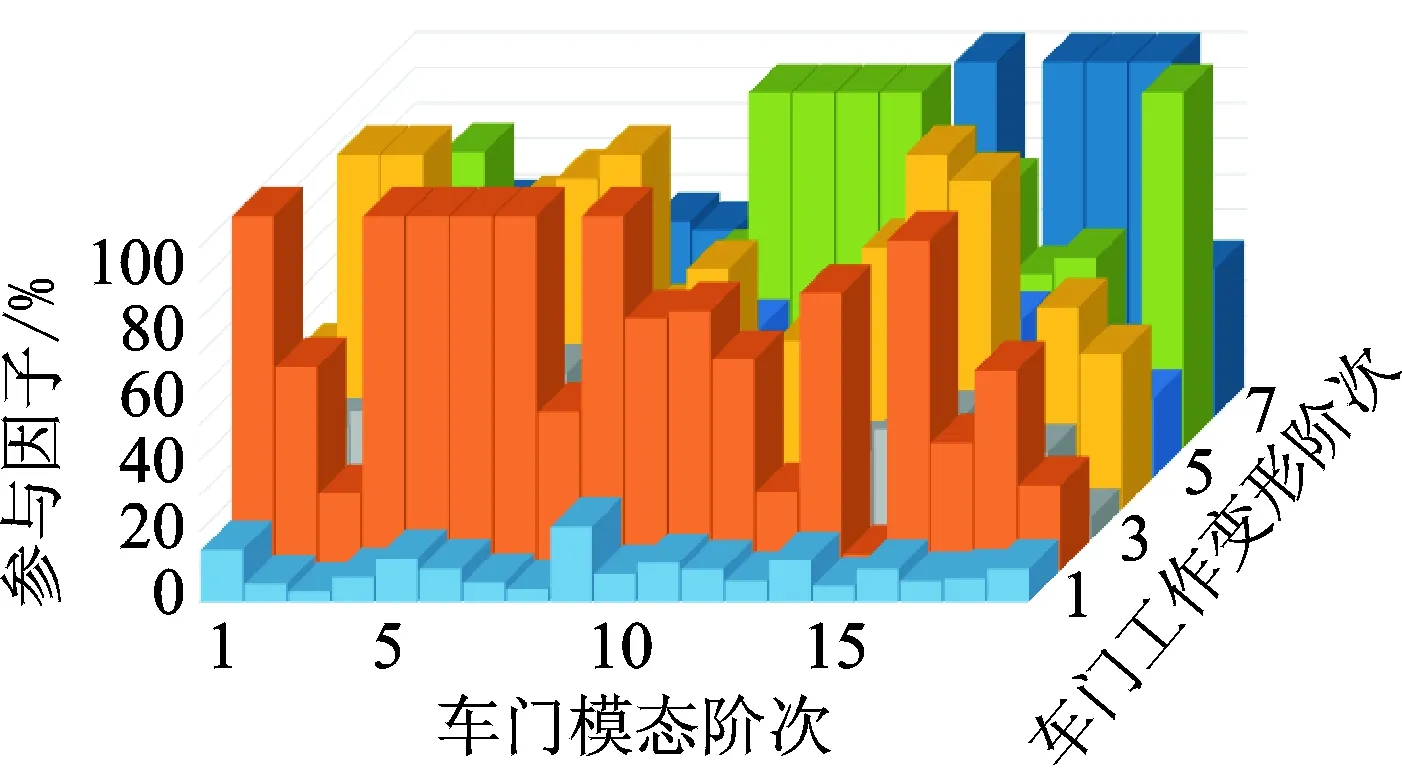
图11 模态参与因子柱状图Fig.11 The modal contribution of ODS

3 改进措施及验证

通过整备车门工作变形试验与半约束模态试验，同时结合STFT时频图分析，研究发现该车门在长期使用后产生关门异响，关门声中产生二次冲击现象。其主要原因是：a.车窗水切、玻璃导轨密封条等非线性元件使用过程中产生性能衰减，导致对车门玻璃的约束减弱，玻璃局部模态振动明显；b.A柱玻璃导轨存在支撑不足的问题，未对车门玻璃起到足够的约束，在工作变形及半约束模态中A柱玻璃导轨均有弯曲变形。

由此对车门玻璃上部粘贴胶棉，从而增加水切压缩量，提升对车门玻璃的约束，如图12所示。

图12 增加水切压缩量Fig.12 Increase the compression of seal

对改进后的关门声进行STFT时频分析，图13为改进后关门声时频图，对比可见，改进后二次冲击现象消失。

图13 改进工况下时频图Fig.13 Time-frequency analysis of optimization

4 结 论

1) 提出了一种基于工作变形模态分解的试验分析方法，依据此方法成功识别出某车型车门异响振动噪声源，并进行了改进试验，验证了此方法的有效性。

2) 车门在下位玻璃状态下关门噪声能量主要分布在低频段，降低振动辐射噪声能有效地抑制关门噪声。

3) 从关门工作变形试验中可以看出，车门结构的振动峰值频率与关门异响频率存在较大的关联。

4) 下位玻璃由于在玻璃顶端缺少足够的约束，在关门过程中易产生较大的振动，引起异响和震颤。

5) 车门玻璃导轨应具有足够的支撑刚度，否则在关门过程中易因刚度不足而引起玻璃及导轨的较大振动，产生关门异响。