基于主曲线相似度的轴承健康状态评估方法*

尹爱军， 梁子晓， 张 波, 王冬磊

(1.重庆大学机械传动国家重点实验室 重庆,400044) (2.中国石油西南油气田分公司重庆气矿工艺研究所 重庆,400021) (3.中国工程物理研究院化工材料研究所 成都,621900)

引 言

旋转机械设备在现代工业中起着不可替代的作用[1]。滚动轴承是旋转机械中重要的部件，是最容易受损的部件之一，它直接影响着旋转机械的性能和运行[2]。

目前，滚动轴承健康状态评估方法的研究受到了学者的广泛关注。苏文胜等[3]将轴承振动信号进行小波包分解后作为滚动轴承故障特征。黄海凤等[4]利用盲源分离后轴承振动信号的峭度值作为轴承性能评估的特征。张云强等[5]提出一种基于中心对称局部二值模式的时频特征提取方法。然而，以上单一特征或对轴承早期故障不敏感，或稳定性差，难以实现滚动轴承状态的准确评估。为此研究人员综合运用时域、频域及小波包时频域的多个特征参数进行状态评估[6]。Shao等[7]提出一种基于局部线性嵌入的连续深度信念网络的方法实现滚动轴承故障检测。Tong等[8]提出了一种基于双树复小波包变换、改进时间尺度分解和极值学习机结合的滚动轴承故障识别新方法。Sohaib等[9]提出了一种基于混合特征模型和深层学习的滚动轴承状态评估方法。李巍华等[10]将小波包熵与高斯混合模型(Gaussian mixture model ，简称GMM)相结合，通过计算各个运行状态对应的GMM相对基准GMM模型的偏离程度来判断轴承的实际退化程度。然而，高维特征集之间往往存在比较强的相关性，有大量的“冗余”信息，并且维数过高，影响后续的算法效率[11]。因此，基于流形学习主曲线将原始高维特征空间转换到低维空间再进行评价等方法得到相关研究[12-13]，这类方法在保留原始数据有效信息量的基础上，消除“冗余”信息，提高效率。

曲线的相似性评价是计算机图形学、模式识别中的中心问题之一,目前主要的判别方法有特征值法和相似性比较法，相似性比较法在一定程度上比特征值法效果好。欧氏距离、马氏距离、Frechet距离都是评估曲线的相似度有效方法，Frechet距离曲线相似性评价表现具有良好的性能[14]。

基于此，笔者提出了一种基于流形空间主曲线Frechet距离相似度的状态评估方法。实验结果表明,该方法克服了单一特征在进行故障诊断时准确率不高的问题，对设备的早期故障更加敏感，且能有效评估滚动轴承的性能退化程度，实现滚动轴承健康状态的定量评估。

1 高维特征流形空间主曲线提取

1.1 高维特征提取

时域特征、频域特征和时频域特征是轴承故障特征的3种类型。时域特征性能不够稳定； 而频域方法作为一种信号整体变换方法，处理对于统计特征随时间不断变化的非平稳轴承故障信号效果并不理想；时频域特征只适用于对缓变信号的分析，作为一种非动态分析方法，对非平稳信号和突变信号的分析有局限[15-18]。

为克服单一特征在表征振动信号特性时存在的片面性及其评估能力的不足，综合运用时域、频域及小波包时频域的高维特征参数进行评估，对滚动轴承全寿命周期振动信号提取时域统计指标、频域统计指标以及小波包能量特征指标，构造融合38个特征量高维特征集[19-20]。

1.2 基于LE流形学习的降维

拉普拉斯特征映射(LE)是一种经典的流形学习算法[21]，可以在获得原始高维数据的低维流形的基础上，同时也能对离群点保持较强的鲁棒性。在高维空间中距离较近的点，在低维空间中也应该距离较近，是一种典型的局部非线性流形学习方法。

给定高维样本集合X={x1,x2,…,xM}T，其中：M为样本点个数；X∈RD。 LE的目标是找到一个最优的流形嵌入。设点集Y={y1,y2,…,yM}T，其中：Y∈RL是X的低维流形表示，Y=F(X)，F则表示空间转换映射

(1)

上述最优化问题进一步转化为求解

ΓF=-div▽‖F‖

(2)

其中：Γ为拉普拉斯特征算子。

若f0,f1,…,fM是上述方程的解，则称其为拉普拉斯特征算子Γ的广义特征向量，且其对应的广义特征值按升序排列为0=λ0≤λ1≤…≤λM， 从而最优的嵌入映射可以表示为F={f1,f2,…,fM}T，因此，高维空间数据X可以映射到低维空间数据Y

Y=F(X)={f1(X),f2(X),…,fM(X)}

(3)

1.3 软-K主曲线提取

主曲线是由Hastie在1984年提出[22]，是流形学习的一个分支，其理论基础是寻找嵌入高维空间的非欧氏低维流形。主曲线是通过数据分布“中间”的曲线[23]，能真实反映数据的形态，即数据集合的“骨架”主曲线是一条通过数据“中心”的自相合光滑曲线。相比主成分分析(principal component analysis，简称PCA)在线性表达上对数据集合的描述，主曲线可以更大程度地刻画数据集的趋势和分布。Verbeek在多边形主曲线的基础上提出了软-K主曲线算法[24],采用局部主成分方法来形成K条线段，并根据光滑性来连接形成主曲线。相对于其他方法，软-K主曲线存在且唯一，曲线估计无偏差，其计算过程较为简捷。

软-K主曲线算法步骤主要分为5步。

1) 初始化。计算数据集X={x1,x2,…,xn}的第1主成分，且设s1=3σ为初始线段(σ为第1主成分标准差)，求出s1的Voronoi区域可表示为V1={x1,x2,…,xn}；K=1。

2) 产生新线段。计算点xk

当mind(xi,sj)-‖xi-xj‖2>0时，则

g(xi,xj)=mind(xi,sj)-‖xi-xj‖2

(4)

当mind(xi,sj)-‖xi-xj‖2≤0时，则

g(xi,xj)=0

(5)

xk的Voronoi区域可表示为

xk={x∈X|x-xk≤mind(xi,sj)}

(6)

计算Vk第1主成分，则sk=3σ；K=K+1；

3) 线段调整。计算新Voronoi区域

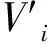
4) 构造优化。用K条线段构造出哈密尔顿路径，并使用2-opt的旅行商问题算法(traveling salesman problem，简称TSP)来优化该路径，其优化目标函数为

其中：l为路径长度。

5) 计算评判函数

(7)

其中：l为步骤4中的哈密尔顿路径；Δ(xi，l)为点xi到l最短距离的平方，通过该评判函数是否收敛来控制迭代结束。

2 基于Frechet距离的主曲线相似性状态评价

2.1 基于Frechet距离的曲线相似性评价

离散Frechet距离是在连续Frechet距离的基础上的一种曲线相似度评估算法，具有良好的性能[25]。

给定两个曲线P={u1,u2,…,up}，Q={v1,v2,…,vq}，P和Q之间的一个单调配对L为一系列对应点(ua1,vb1)(ua2,vb2),…,(uam,vbm)，其中a1=1,b1=1,am=p,bm=q，对所有的i=1,2,…,m，当且仅当下面是3个中的1个成立

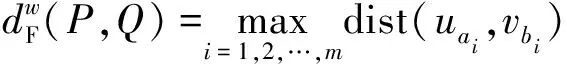
(11)

其中：dist(uai,vbi)为uai,vbi间的欧氏距离。

曲线P和Q间的离散Frechet距离为

(12)

距离数值越小，表明曲线P和Q越相似。

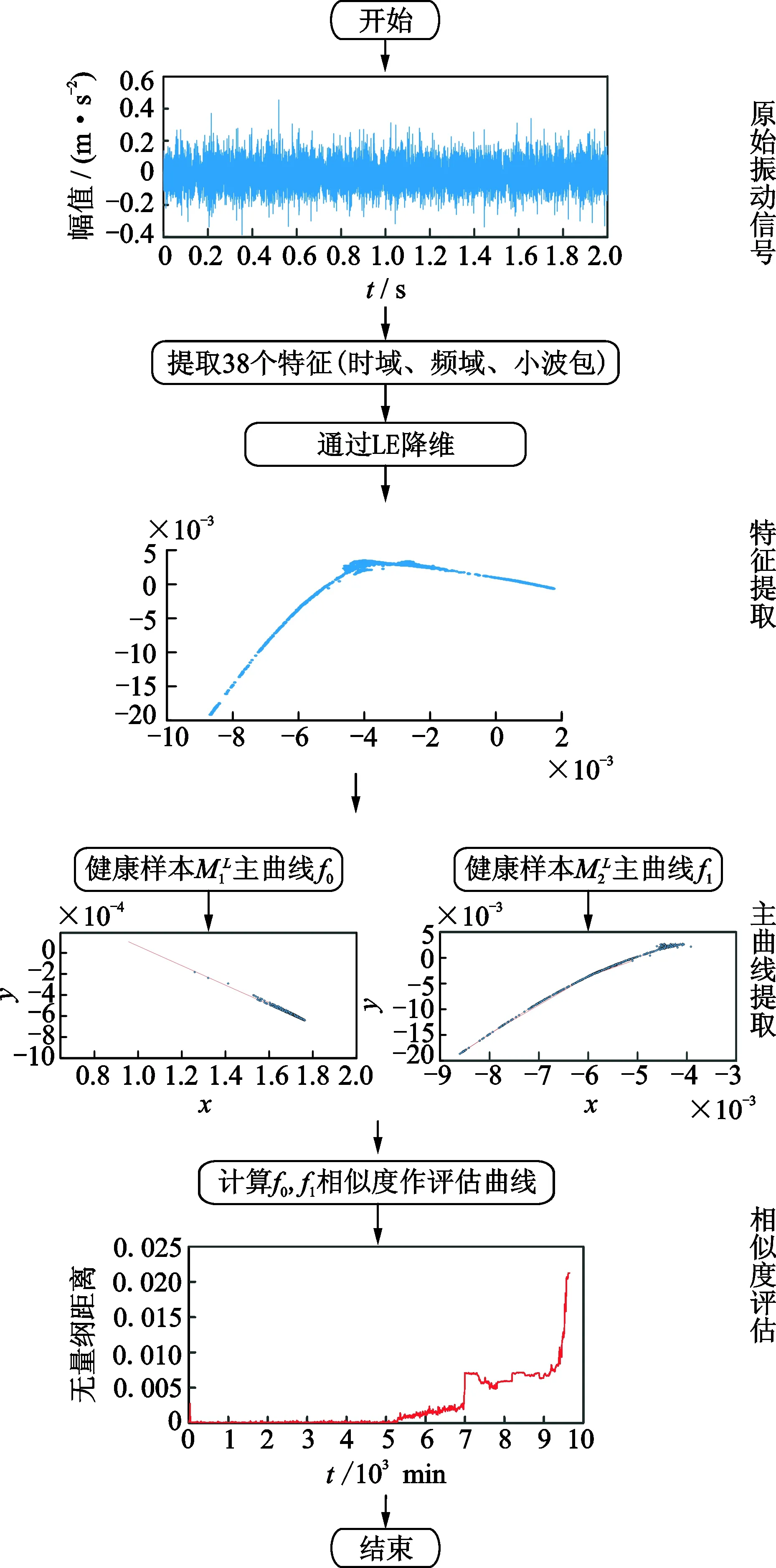
图1 滚动轴承性能退化评估方法流程图Fig.1 A flow chart for evaluating the performance degradation of rolling bearings

图2 滚动轴承加速度退化实验系统Fig.2 Experimental system of accelerated degradation of rolling bearing

2.2 滚动轴承性能退化评估流程

以开始阶段的健康样本主曲线作为基准主曲线，通过计算各阶段样本主曲线和基准主曲线的离散Frechet距离，实现对轴承退化的定量评估,流程如图1所示。

3 对比实验分析

3.1 滚动轴承健康状态评估实验系统

实验数据来自于美国辛辛那提大学IMS实验室，轴承实验装置如图2所示，4个ZA-2115双列滚子轴承安装在测试台，由交流电机通过摩擦带轮驱动旋转，转速恒定为2 kr/min，在测试台横梁施加2 722 kg径向载荷，以磁性塞累积磨损碎片反映轴承退化程度，当累积碎片量超过一定阈值时，停止实验。历时9 840 min后，轴承1出现外圈故障。实验采集轴承座的加速度振动信号，采样频率为20 kHz。

3.2 滚动轴承健康状态评估

滚动轴承性能退化状态一般分为初始故障状态、中度故障状态以及深度故障状态[19]。 针对实验中滚动轴承全寿命周期数据，选取前600 min作为健康样本，600 min至实验结束均为测试样本，评估滚动轴承性能状态变化。

图3分为轴承健康样本与测试样本的流形空间二维主曲线。由图3 (a)和(b)可知，运行早期，主曲线形状与趋势比较相似；而后期轴承会产生磨损等缺陷，因此，所提取的主曲线有明显的差异，如图3(c)所示。

图4为3种不同“距离”评价下所得到的轴承状态评估曲线。从图4中的3条轴承状态评估曲线变化趋势可看出，轴承从开始运行到5 000min左右相当长的一段时间内，“距离”评估值很小，接近于0，且趋势变化平稳，表明滚动轴承性能状态良好。 评估曲线a在5 200 min左右时，有明显上升， 偏离正常状态，轴承开始进入初始性能退化状态。 曲线b，c分别在6 400和6 500 min左右才检测到轴承的初始性能退化状态。Frechet距离对轴承早期故障更敏感。

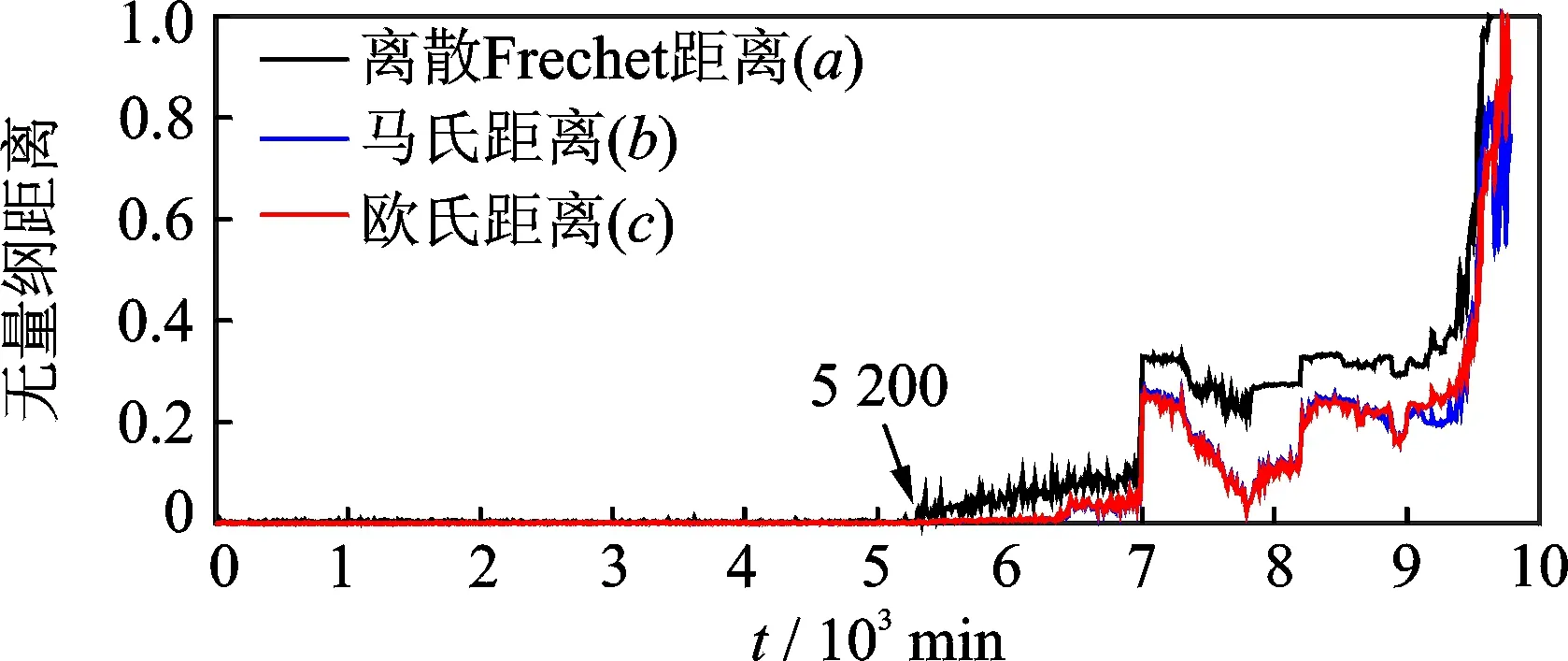
图4 不同“距离”状态评估曲线对比Fig.4 Comparison of different “distance” state assessment curves

在7 000 min左右，3条曲线均有非常明显的上升趋势，显示滚动轴承开始进入中度性能退化状态。在7 000～9 500 min左右，曲线呈现下凹趋势，实质为出现故障而故障又被消除的过程[26]。 曲线b和c的距离评估指标在下凹阶段与初始故障状态的评估值有重叠，非常容易产生状态识别错误，而曲线a并无重叠，表明笔者所提方法对中度性能退化状态评估更好。

在9 500～9 800 min左右，曲线b，c中的距离评估指标出现震荡，虽然呈现上升趋势，但与中度性能退化状态相比并无明显区别，无法实现对滚动轴承健康状态的定量评估。而曲线a有明显上升趋势，表明滚动轴承进入深度性能退化状态，此时轴承已经基本失去工作特性，直至到 9 800 min左右最终完全损坏失效。由此可知，笔者所提距离评估指标对轴承初始性能退化状态较敏感；在故障点平滑的下凹阶段与初始退化指标无重叠现象，且误估率很低；同时，对轴承深度故障及失效状态能够进行准确的评估。因此，本研究方法具有更好的评估效果。

作为非线性降维算法的代表，局部线性嵌入 (locally linear embedding ,简称LLE)能够使降维后的数据较好地保持原有流形结构，而线性判别分析 (linear discriminant analysis，简称LDA)是一种经典的有监督的线性降维算法。本研究方法与LLE及LDA对比如图5所示。对比分析3种降维方法，LLE算法随时间变化呈现出明显的波动，对轴承振动信号比较敏感，能大致反映出轴承的运行状态与退化趋势，但波动过大，不能准确识别故障程度；而LDA算法对滚动轴承性能退化状态的评估曲线对轴承故障不敏感。直到9 800min左右轴承完全失效，评估曲线才出现上升，评估效果并不理想。

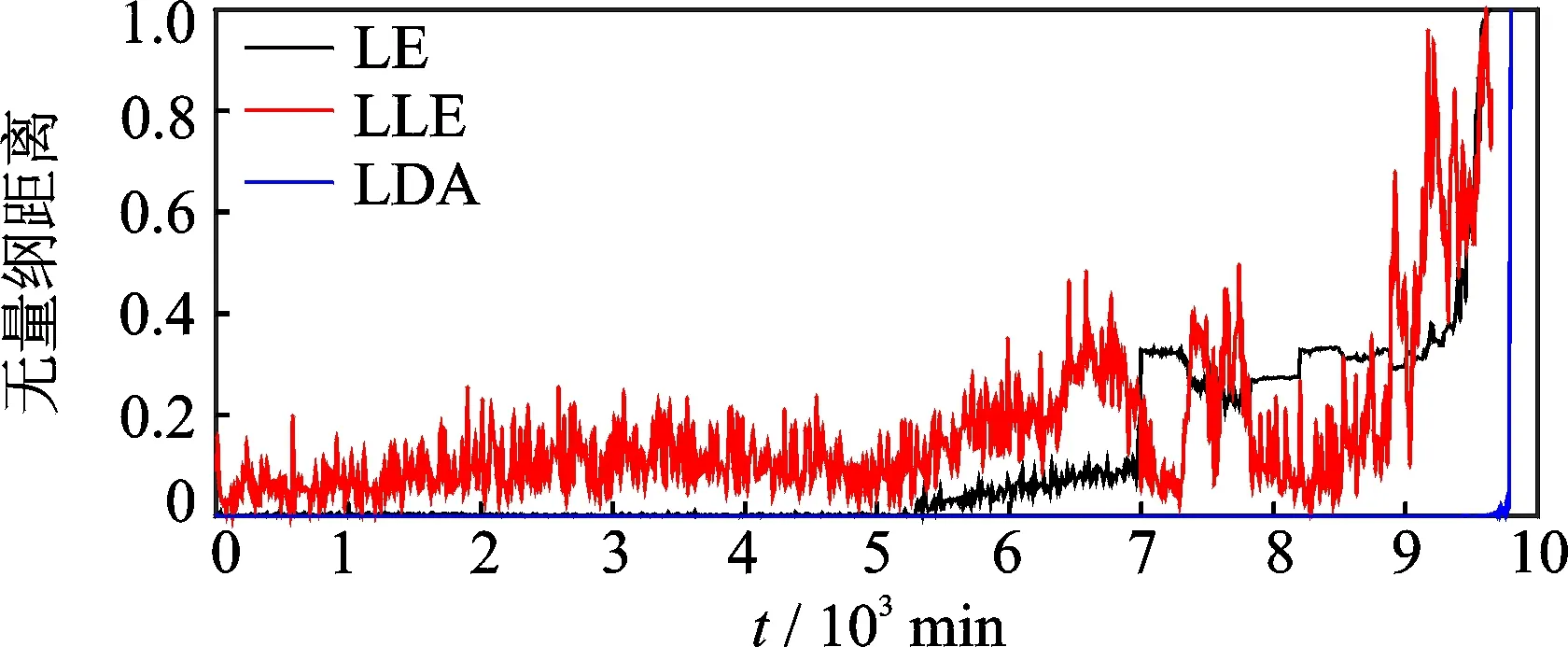
图5 不同流行学习算法状态评估曲线对比Fig.5 Comparison of different characteristic spatial state assessment curves

3.3 对比分析

基于概率以及机器学习的算法在机械设备故障诊断、状态评估等领域得到较多研究[7-9]。本研究方法与HMM及DBN对比如图6所示。其中： HMM选取隐含状态数为2，混合高斯函数个数为3；DBN选取2层隐含层，各层节点个数为100。

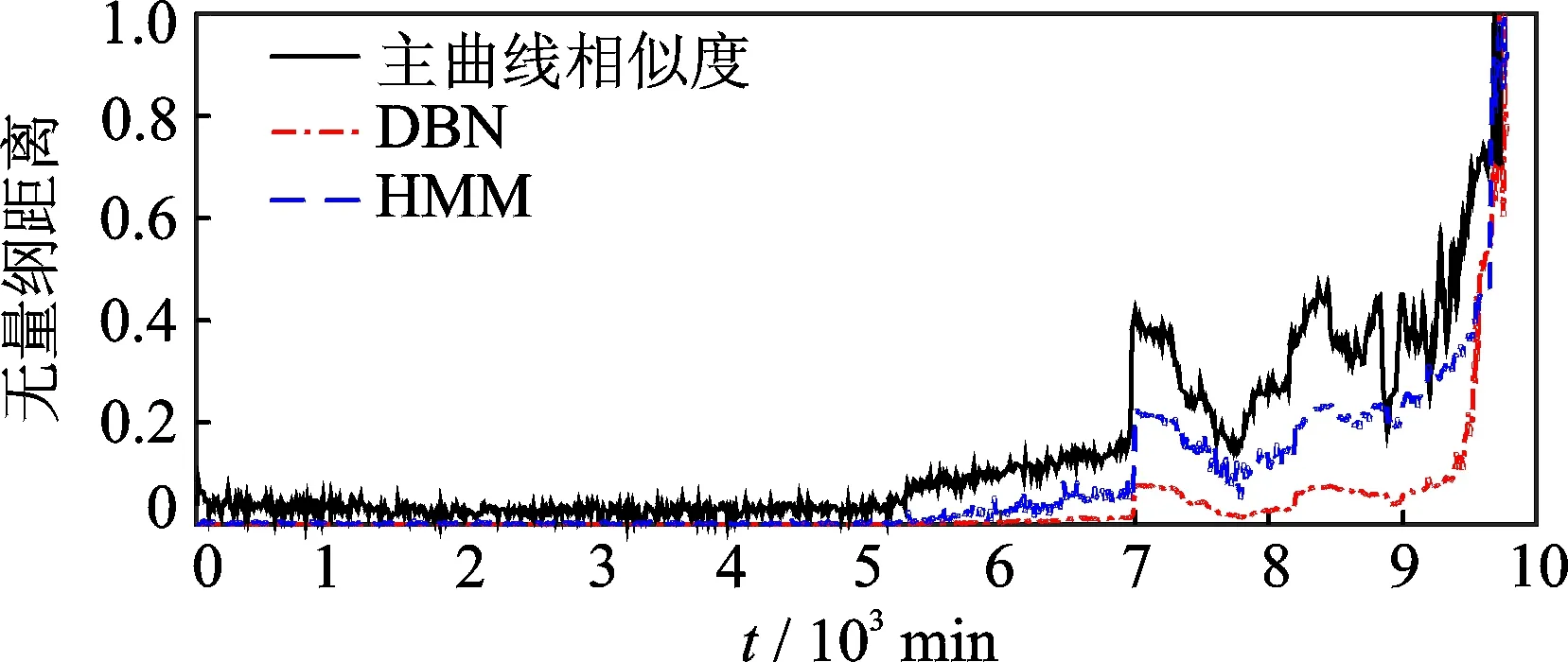
图6 状态评估方法实验对比Fig.6 Experimental comparison of state assessment methods

由图6可以看出，在5 000～6 000min之间，归一化幅值无明显变化，表明HMM与DBN模型对轴承早期故障不敏感；在7 000min之后，只有波动，没有类似主曲线评估算法中突变-回落-波动的过程，即无法准确描述轴承故障加深逐渐磨平的运行状态。相比较而言，这两种方法均能在一定程度上描述滚动轴承的状态变化趋势，但均没有本研究基于主曲线相似度的方法更准确，且不能发现轴承的早期故障。

定量分析3种方法，为此分别比较了评估曲线值变化率，表1为曲线值变化率为2%，5%时3种方法所用的时间对比。

表1 评估曲线值变化率对比

Tab.1 Comparison of the rate of change of the value of the evaluation curve

/%/minDBN/minHMM/min255 3206 5306 8806 9906 8907 010

由表1可以看出，主曲线相似度方法可以更快达到2%，5%的变化率，可知主曲线相似度对轴承振动信号以及早期故障更敏感。

4 结束语

针对单一特征在表征振动信号特性时存在的片面性及其评估能力的不足，融合多分析域特征，提出一种基于流形空间主曲线相似度的滚动轴承健康状态评估方法，该方法能够有效描述滚动轴承全寿命周期的性能退化规律。所提方法克服了单一特征监测结果的不稳定，能够对滚动轴承健康状态进行定量评估，性能退化趋势更为直观。相对于欧式距离等距离评估方法，对早期损伤更敏感。本研究所提方法仅涉及低维流形空间中主曲线的提取，后续研究将考虑更高维度流形空间。