三维蜂窝状声子晶体的带隙优化研究*

邵瀚波， 陈国平， 何 欢

(南京航空航天大学航空宇航学院 南京，211100)

引 言

声子晶体是内部组元的弹性常数、密度以及声速周期性变化的一种具有带隙的声学功能材料，当弹性波频率在声子晶体带隙范围内时，弹性波将被抑制或禁止传播，所以较宽的低频带隙对于减振降噪提供了新的方法和思路[1]。

声子晶体由于在控制弹性波方面具有很好的物理特性，吸引了广泛的关注[2-3]。理论和实验结果都表明，声子晶体中可以出现完整的带隙[4-7]，这些带隙可以用来减振或者控制环境的噪音[8-10]，其中主要分为布拉格散射型[11-12]和局域共振型带隙[13]。局域共振型声子晶体与布拉格散射型声子晶体不同，其可以用较小尺寸获得低频带隙[14-15]，这一特点使得声子晶体在低频减振降噪方面很有理论价值和应用前景。

由于声子晶体的带隙特征对减振降噪具有非常重要的价值，国内外在声子晶体带隙的计算方面研究较多[16-18]。声子晶体的带隙范围由晶体结构特征决定，根据带隙与晶体结构形式之间的关系可以对声子晶体的构成参数或结构特征进行优化设计，使声子晶体具有最佳的带隙特征，从而得到具有更好的减振降噪性能的声子晶体。温熙森[19]研究了二维平面蜂窝状晶体结构的声子晶体，选用钢作为散射体，丁腈橡胶作为基底，分析了局域共振型声子晶体的原胞并运用集中质量法计算出能带结构，并与三角形晶格状声子晶体进行比较，得出了其带隙分布主要在200～270 Hz之间。笔者在此基础上，研究了三维蜂窝状声子晶体，并通过对参数以及结构进行优化设计，得到了最优的蜂窝状声子晶体，可以对带隙范围进行调控，从而满足不同的频率要求。

1 声子晶体的模型与计算方法

图1为4种蜂窝状结构的声子晶体，基体是用丁腈橡胶制作的三角形晶格板，在中间挖去孔并嵌入圆柱形的钢作为芯体。其晶格常数a=0.01 m，孔半径为r，板厚度为h，芯体高度为t。钢和丁腈橡胶的材料参数如表1所示。

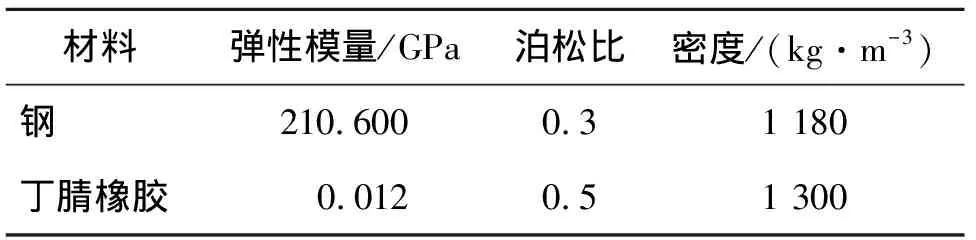
表1 各材料参数

图1 不同蜂窝状结构声子晶体Fig.1 Phononic crystals with different structures

通过有限元方法来计算三维蜂窝状结构声子晶体的离散关系，将其中一个晶胞划分有限元网格，把问题转化为一般的特征值问题。

对于一个晶胞的特征方程可以表示为

(K-ω2M)U=0

(1)

其中：U=[U1U2…Un]T为节点的位移矩阵，且Ui=[uiviwi]T；K和M分别为单元刚度和质量矩阵。

根据布洛赫定理，弹性结构的位移场u(r)可以表示为

u(r)=uk(r)e(ikr)

(2)

其中：k=(kx,ky)为不可约布里渊区波矢量；r=(x,y,z)为节点坐标矢。

uk(r)晶胞中有相同周期边界条件的矢量式，根据布洛赫理论，通过式(2)可以得到周期边界条件

U(r+a)=U(r)e(ika)

(3)

其中：a为晶格常数。

通过COMSOL软件来计算分析上述蜂窝状结构声子晶体的特征频率，从而分析相对应的能带结构和振动模式以及传输特性。传输特性方程定义为

H=10log(u1/u2)

(4)

其中：u1和u2分别为激振位移和传递到边界的位移。

传递方式如图2所示，在蓝色阴影边界施加“1”

图2 声子晶体施加边界加速度Fig.2 Exerts a boundary acceleration to phononic crystal

的加速度，方向垂直于边界面沿板面方向，其余边界均为自由边界条件。

2 结果和分析

2.1 不同蜂窝状结构声子晶体对带隙的影响

在二维蜂窝煤状声子晶体模型的基础下，笔者通过对4种三维不同蜂窝状结构的声子晶体建模并利用COMSOL进行计算，验证了各种声子晶体的能带结构，分析了位移模式以及传输特性。

图1中设置板厚度h=3 mm，散射体高度t=18 mm，半径分别为10，8，6和8 mm。将波矢k在不可约Buillouin区边界上取值，M，X和Γ为其中3个顶点，计算出能带结构。由图3可以看出：当散射体只有1个或者2个芯体时，出现的带隙较宽，分别为605.89～985.42 Hz和1 041.45～1 492.8 Hz；而当有3个芯体或者有1个缺陷芯体时，出现的带隙很窄。这表明在此频率范围内的弹性波传播被抑制，而其他频率范围(通带)的弹性波可以无损耗地进行传播。

图4所示为声子晶体的振动模式俯视图(分别含有1个、2个、3个芯体及1个芯体缺陷的蜂窝状结构)，其中前4幅为带隙下边缘，后4幅为带隙上边缘。由图4的位移模式可以看出，不管是带隙上边缘还是下边缘，主要振动都出现在橡胶板上，在1个芯体声子晶体的带隙下边缘激励以及接受边上出现弯曲振动，而上边缘只有1个角上出现纵向位移。相同的，对于2个芯体的声子晶体的带隙上边缘，有2个角出现很大的纵向位移，而下边缘4个角的纵向位移都很平均。对于有1个芯体缺陷的声子晶体，带隙下边缘和2个芯体时情况类似，而上边缘只有缺陷出现很大的纵向位移，这些位移变化导致了两种声子晶体带隙的存在。相反的，对于3个芯体的声子晶体，位移变化不大，导致带隙也不是很明显。

图2中，选取8×8周期结构声子晶体并采用四面体网格，利用式(4)计算其传输特性(transmission loss，简称TL)。如图5所示 ，可以看出箭头及阴影范围内输出端的响应明显减少，说明该频率范围的幅频特性明显衰减，通过与带结构图对比可以验证其减振效果。

本节内容验证了在蜂窝煤状声子晶体中，对于1个及2个芯体的声子晶体具有更好的减振效果，和二维平面的结果类似，但是比二维平面情况得到更宽的带系范围，减振效果更好。

图3 不同蜂窝状结构声子晶体能带结构Fig.3 Band gaps with different structures

图4 声子晶体的振动模式俯视图Fig.4 The vibration mode of the phononic crystals

2.2 芯体几何参数对带隙的影响

2.2.1 芯体高度对带隙的影响

选取2个芯体的声子晶体进行研究，分别设置芯体的高度为3，9和18 mm，其他条件不变，用COMSOL模拟出的能带结构以及传输特性如图6所示。可以看出，当t=3 mm时，仅仅在1 700 Hz左右出现1条很窄的带隙；而当t=9 mm时，能带结构有所改善，除了1 600 Hz左右有1条很窄的带隙之外，1 148.46～1 398.25 Hz之间还出现一条比较宽的带隙；当t=18 mm时，高频的窄带隙消失了，出现了1条从1 041.45～1 492.8 Hz的带隙，能带结构有明显改善，说明当t=18 mm时具有更好的减振特性。图6中的传输特性图和能带结构基本吻合，也验证了这一结果。

2.2.2 芯体半径对带隙的影响

在t=18 mm的基础上改变声子晶体芯体的半径，由于r=2 mm时，结构不存在带隙，所以考虑3～10 mm半径对带隙的影响。通过计算发现，其能带结构主要出现在第13～14阶固有频率中间，如表2所示。由图7可以看出，改变半径时，带隙下边缘值基本保持不变，维持在1 000 Hz左右。上边缘值波动很大，当r=3，5，10 mm时，较接近下边缘，直接导致了带隙很窄；而当r=4，6，8和9 mm时，带隙上边缘较远离下边缘，所以出现的带隙较宽，尤其是当r=8 mm时，带隙最宽，得到最优的能带结构。

图8所示的振动模式中，(a)～(c)为带隙下边缘，(d)～(f)为带隙上边缘。由图8可以看出：当r=3 mm时，第13阶的振动幅度很小且集中在声子晶体内部，而14阶主要集中在激励边和接受边上，表现为很大的弯曲振动；当r=6 mm时，带隙的上下边缘振动位置正好相反，都变现为较强的纵向振动；当r=9 mm时，下带隙主要表现为4个角的弯曲振动，而上带隙则偏向激励边上的振动，且振动幅度变小很多。

图5 不同蜂窝状结构声子传输特性Fig.5 The transmission loss of structures

图6 不同高度芯体的声子晶体能带结构和传输特性图Fig.6 The phononic crystal band structure and transmission loss of cores in different height

图7 不同半径声子晶体的带隙上下边缘值折线图Fig.7 The edge values of the band gap of different phononic crystals′radii

图8 不同半径下声子晶体的振动模式Fig.8 Vibration mode of phonon crystals in different radii

2.3 橡胶几何参数对带隙的影响

2.3.1 橡胶高度对带隙的影响

在保持芯体高度t=18 mm和r=8 mm的条件下，改变橡胶的高度分别为2，3和5 mm，分析对带隙的影响，如图9所示。

图9 不同高度橡胶的声子晶体能带结构和传输特性图Fig.9 The phononic crystal band structure and transmission loss of rubber with different height

通过计算发现，随着高度的增加，带隙的宽度没有实质性的变化，但是带隙的上边界值和下边界值都有所增加(只考虑第13阶固有频率到14阶固有频率之间的带隙)，具体数值见表2。当r=2 mm时，带隙范围为805.62～1 250.34 Hz，相比较其他的带隙而言，能得到较低的能带结构，且带隙宽度也不会减少，传输特性图也表明了在这区间，响应得到明显衰减；当r=3 mm时，带隙增加到1 041.45～1 492.8 Hz；当r=5 mm时带隙增加至1 397.56～1 785.54 Hz。通过计算分析得知，如果要得到比较低的带隙频率，必须降低橡胶高度，当r=2 mm时，对于低频的减振效果最明显。

表2 不同半径时声子晶体的带隙上下边缘值

Tab.2 The upper and lower edge values of phononic crystals in different radii

r/m13/Hz14/Hz0.0030.0040.0050.0060.0070.0080.0090.0101 060.871 062.431 048.381 003.12987.491 041.451 004.561 009.811 120.701 297.561 128.791 295.431 198.601 492.801 403.211 208.10

计算分析表明，可以通过调节橡胶的高度对声子晶体的带系在2 000 Hz之内达到可调节化，随着橡胶高度从2～5 mm之间变化，带隙下界限从805.62 Hz变化到1 397.56 Hz。通过这一理论，对于不同的减振需求可以选择不同的声子晶体。

2.3.2 减少橡胶刚度对带隙的影响

在维持橡胶高度为3 mm的条件下，为减少橡胶刚度，在模型的4个角分别挖去半径为8 mm的部分圆形，构成如图10的模型。对其进行进一步分析表明，由图11的能带结构可以看出，减少了橡胶刚度后，原本1 041.45～1 492.8 Hz的带隙被分成了两个很窄的带隙，并且1 446.78～1 702.36 Hz之间出现了一条比较高的带隙，导致结构对低频减振性能的降低，通过传输特性图也可以验证这一点。

图10 减少橡胶刚度后的声子晶体Fig.10 Phononic crystal that the stiffness of rubber is reduced

图11 减少橡胶刚度后声子晶体能带结构和传输特性图Fig.11 The structure and transmission loss of the phononic crystal that the stiffness of rubber is reduced

3 结 论

1) 改变芯体的高度时，当t=18 mm得到的带隙范围更宽且频率相对较低，相对其他高度而言具有最好的减振性能。

2) 芯体的半径不同，带隙的范围波动不定，但是带隙下边界基本保持不变，上边界在r=8 mm时出现最大值，且位移模式以弯曲振动和纵向振动为主。

3) 随着橡胶高度的增加，带隙范围变化不大，但是带隙频率一直在增高，所以通过调节橡胶的高度，可以满足不同频率范围的减振效果，从而可以针对不同的减振需求达到带隙范围的可调节化。

4) 在四周挖去4个角来减少橡胶的刚度对于声子晶体的带隙影响效果不大，具体刚度对带隙的影响还需要做进一步研究认证。