带有不同Hardy项的椭圆方程组的Mountain-Pass解

康东升,高蒙, 刘晓楠, 曹玉平

(1 中南民族大学 数学与统计学学院, 武汉 430074； 2 中南民族大学 图书馆, 武汉 430074)

1 相关知识及假设

本文主要研究下列临界椭圆方程组：

(1)

其中Ω⊂N(N≥3),0∈Ω是光滑有界区域, 参数满足以下条件：

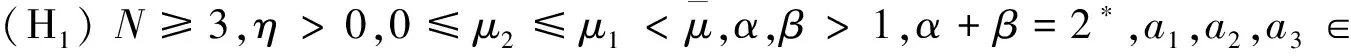
(2)

这里E(u,v):=|u|2+|

F(u,v):=|u|2*+|v|2*+η|u|α|v|β,

Q(u,v):=a1u2+2a2uv+a3v2.

因此能量泛函J∈C1(H×H,). 我们称(u,v)∈H×H{(0,0)} 是方程(1)的解, 如果

(u,v)≠(0,0)，J′(u,v),(φ,φ)=0,∀(φ,φ)∈H×H,

这里J′(u,v)是能量泛函J在点(u,v)的Fréchet导数.在(H1)的假设下, 由Hardy, Sobolev和Young不等式, 我们可以定义如下最佳Sobolev常数[2-4]:

S(μ1,μ2)=

这里D=(D1,2(N))2{(0,0)},D1,2(N)是N)关于·|2dx)1/2的完备化.

近年来, 许多学者研究了带有Hardy不等式和临界非线性的椭圆方程组(参见[2-7]). 在文献[4]中, Terracini证明了最佳常数S(μ)的达到函数为:

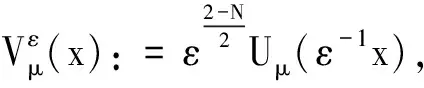
其中Uμ(x)是如下的径向对称函数:

在(H1)的假设下, 我们定义如下常数:

除(H1)外, 还定义下列假设：

(H2)β<2或者η>η*.

我们得到的新结果归纳为以下定理.

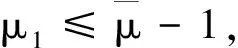
本文用到以下符号和定义:o(1)表示一个无穷小量,O(εt)满足|O(εt)|/εt≤C(任意ε>0足够小), 特别地,o(εt) 表示当ε→0时,|o(εt)|/εt→0,O1(εt)表示存在常数C1,C2>0使得C1εt≤O1(εt)≤C2εt. 我们将正常数表示为C, 有时省略积分中的dx.

2 引理及证明

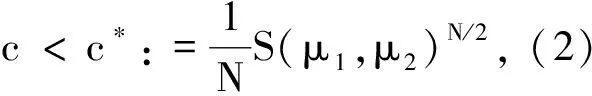
证明证明过程类似于文献[6]中引理2.1, 这里略去.

假设 (H1)成立, 考虑如下椭圆方程组:

(3)

需要指出的是, 文献[2]首次介绍了方程组(3), 文献[3]证明了方程组(3)径向对称且严格递减解的存在性, 文献[8]则证明了方程组(3)径向对称且严格递减的解的渐近性质.

引理2[3]假设(H1)和(H2)成立, 则最佳常数S(μ1,μ2)存在一个正的径向对称严格递减的达到函数对(U(x),V(x)).

引理3[8]假设(H1)成立, (u,v)∈

(D1,2(N))2是方程组(3)正的径向对称严格递减的解. 设r=|x|.

1)另外假定(H4)成立, 则存在常数Ci>0,1≤i≤4, 使得：

(4)

2)另外假设(H5)成立, 则u满足(4)式, 且存在常数ci>0,1≤i≤6 , 使得v满足：

3 解的存在性

设(U(x),V(x))是在引理2中得到的最佳常数S(μ1,μ2)的径向对称严格递减的达到函数对. 定义：

引理4假设(H1)和(H2)成立.

(i) 则有：

(ii) 进一步假设(H4)成立, 则：

(iii) 进一步假设(H5)成立, 则：

证明假设(H5)成立, 直接计算可得：

通过讨论发现当条件(H1),(H2),(H5)成立的情况与条件(H1),(H2),(H4)成立的情况相同. 我们仅在假设条件(H4)成立的基础上证明(i)的第一个等式和第二个等式. 其他情况也可以类似地证明(过程略).

假设条件(H1), (H2), (H4)成立, 因为(Uε(x),Vε(x))是S(μ1,μ2)的达到函数对,则：

(5)

由(5)式、引理2和引理3有：

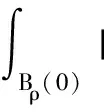
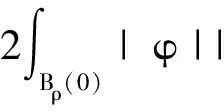
|φ||φ||Vε||Vε|dx=

|x|-2b(μ2)-2dx+

如果(H4)成立, 则有：

证毕.

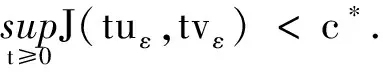
证明我们只证明当(H4)成立的情况, (H5)成立时的证明过程类似.

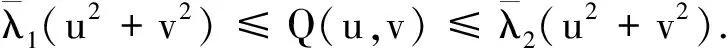
可以得到:

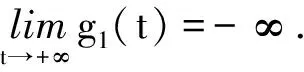
(6)

(7)

由(6), (7)式和引理4有：

引理5证毕.

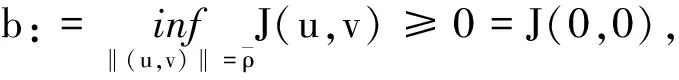
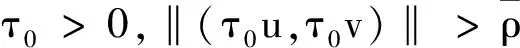
满足引理1条件的{(un,vn)}存在子序列, 仍记为{(un,vn)}, 使得在H×H中,(un,vn)→(u,v). 因此，(u,v)是能量泛函J的临界点, 且(u,v)是方程组(1)的解,c是其对应的临界值.