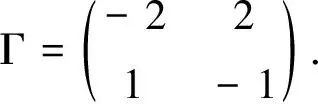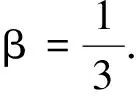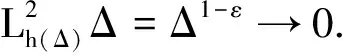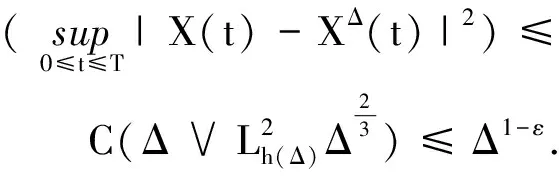混杂随机泛函微分方程修正截断EM算法的强收敛率
2019-06-25胡军浩方明高帅斌
胡军浩,方明,高帅斌
(中南民族大学 数学与统计学学院,武汉430074)
1 相关知识
考虑混杂随机泛函微分方程
dX(t)=f(Xt,Λ(t))dt+g(Xt,Λ(t))dB(t),
0≤t≤T,
(1)
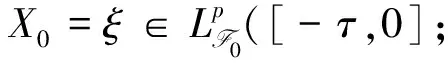
f:C([-τ,0];n)×S|→n,
g:C([-τ,0];n)×S|→n⊗m
是可测函数,B(t)=(B1(t),B2(t),…,Bm(t))T是定义在完备概率空间(Ω,F,{Ft}t≥0,P)上的m维Brownian运动.Λ(t)是右连续的Markov链,取值于有限状态空间S={1,2,…,N},其生成元Γ=(γij)N×N表示为:
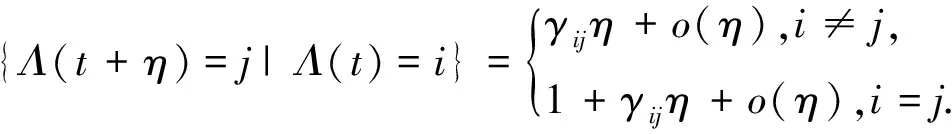

方程(1)的参数满足下列条件:
(A1)对于任意的R>0,存在一个LR>0,使得:
|f(φ,i)-f(ψ,i)|∨|g(φ,i)-g(ψ,i)|≤
LR‖φ-ψ‖,
其中φ,ψ∈C([-τ,0];n),‖φ‖∨‖φ‖≤R,i∈S.
(A2)存在p≥2,K>0,使得:
K(1+‖φ‖2),g(0,i)≡0,
其中φ∈C([-τ,0];n),i∈S.
(A3)存在q≥2,H>0,使得:
|g(φ,i)-g(ψ,i)|2≤H‖φ-ψ‖2,
其中,φ,ψ∈C([-τ,0];n),i∈S.
(A4)对于任意的ϑ>1,初值ξ满足E|ξ(t)-ξ(s)|2ϑ≤C|t-s|ϑ.
为定义修正截断EM算法,选取充分小的Δ*>0和严格正的递减函数h:(0,Δ*]→(0,∞),使得:
(2)
(3)
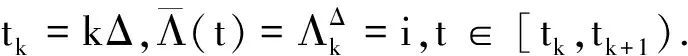
(4)
对于非线性随机微分方程数值解,Mao X.首次提出截断EM算法,讨论其强收敛性和收敛率问题[1,2].文献[3,4]在截断EM算法基础上加以修正,提出修正截断EM算法,讨论随机微分方程数值解的强收敛性和渐近指数稳定性问题.
由于泛函的引入,随机微分方程数值解强收敛和稳定性研究会变得比较复杂[5,6],文献[7,8]为了改善算法复杂度提出了时间上截断的EM算法,讨论随机泛函微分方程解的存在性和唯一性.
在文献[3]和文献[8]的基础上,提出在空间上和时间上都截断的EM算法,讨论混杂随机泛函微分方程数值解的强收敛率问题.强收敛率主要依赖于Markov切换.同时,这种算法改善了泛函带来的复杂度.
2 基本引理
引理1[9]若条件(A1)和(A2)成立,方程(1)有唯一的解X(t),且


其中C是依赖于T,p,K,ξ的正常数.
引理2[9]对于停时
σR=inf{t≥0:|X(t)|≥R},infφ=∞.
若条件(A1)和(A2)成立,则:


利用文献[12]类似的方法,给出截断函数fΔ和gΔ的性质.

|fΔ(x,i)-fΔ(y,i)|∨|gΔ(x,i)-gΔ(y,i)|≤4Lh(Δ)‖x-y‖,
(5)
其中x,y∈C([-τ,0];n),i∈S.
引理5若条件(A2)成立,则对于任意固定的Δ∈(0,Δ*]和h(Δ)≥1,有:
2K(1+‖x‖2),
(6)
其中x∈C([-τ,0];n),i∈S.
引理6若条件(A1)和(A2)成立,则对于任意固定的Δ∈(0,Δ*]和h(Δ)≥1,有:
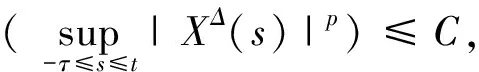
(7)
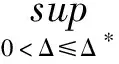
(8)
其中C是依赖于T,p,K,ξ的正常数.

(9)
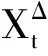

计算:

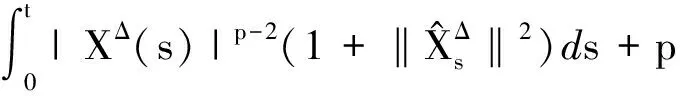
‖ξ‖p+J1+J2+J3.
(10)
注意到:
由引理4有:
4Lh(Δ)‖ξ‖+h(Δ).
(11)
由Young不等式有:
因此,


再次应用Young不等式和(11)式,有:




利用不等式(a+b)p≤2p(ap+bp),a,b>0,p>1可得:



由Burkhold-Davis-Gundy不等式、Young不等式和(11)式可得:

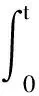
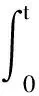
把J1,J2,J3代入(10)式可得:

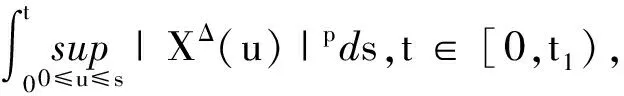
其中C1,C2是依赖于T,p,K,ξ的正常数.
由Gronwall不等式可得:
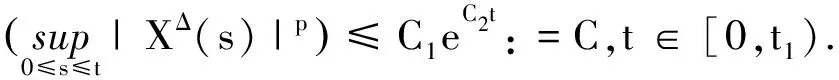
对于t∈[0,t1)有:


对于t∈[t1,t2)有:


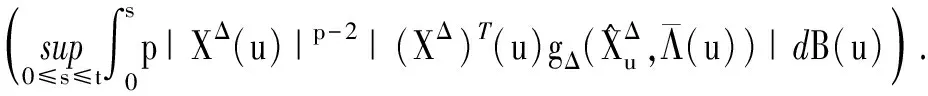
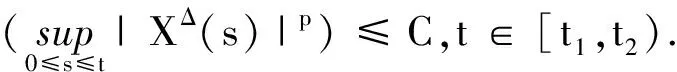
经过步长Δ的向前递推有:

因此,


t∈[tk,tk+1).证毕.
由引理6以及引理2的相似结论可以得到下面的引理.
引理7定义停时
ρΔ,R=inf{t≥0:|XΔ(t)|≥R},infφ=∞.
若条件(A1),(A2),(A4)和(2)式成立,则对于任意的R>‖ξ‖和Δ∈(0,Δ*),有:
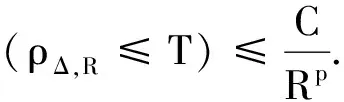
(12)
引理8若条件(A1),(A2)和(2)式成立,则对于任意固定的Δ∈(0,Δ*]和h(Δ)≥1,都有:
(13)
其中C是依赖于T,p,K,ξ的正常数.
引理9若条件(A1),(A2)和(2)式成立,则对于任意固定的Δ∈(0,Δ*]和h(Δ)≥1,使得当0≤s (14) (15) 其中C是依赖于T,p,K,ξ的正常数. (16) 其中C是正常数. E|XΔ(t)-XΔ(s)|2p≤C|t-s|p. 则对于任意的0≤t≤T,有: 引理11若条件(A1),(A2)和(2)式成立,则对于任意固定的Δ∈(0,Δ*]和h(Δ)≥1,有: (17) 其中C是依赖于T,p,K,ξ,Γ的正常数. 证明由条件(A1)和引理6可得: 根据Markov性质可得: EI{Λ(s)≠Λ(tk)|Λ(tk)}= 故: 其中C是依赖于T,p,K,ξ,Γ的常数.同理可得第2个不等式.证毕. 其中δΔ,R:=σR∧ρΔ,R. 证明记δ=δΔ,R,e(t)=X(t)-XΔ(t).由It公式和Burkhold-Davis-Gundy不等式可得: 因此, 因为0≤s≤t∧δ,‖Xs‖≤R≤h(Δ),所以 根据基本不等式可得: 和 因此, (18) 根据Young不等式、引理4和引理10可得: (19) 同理可得: (20) 由Young不等式和引理11可得: (21) 和 (22) 再次应用Young不等式和引理4可得: (23) 把(19)~(23)式代入(18)式可得: 其中C和C1是依赖于p,q,T,H,Γ的两个正常数.应用Gronwall不等式即可得到需要的结论.证毕. 证明根据Young不等式,∀ε>0,有: 由引理1和引理6可得: 同时,由引理2和引理7可得: 因此, 例1考虑带有Markovian切换Λ(t)的非线性随机泛函微分方程,其中Λ(t)取值于S={1,2},生成元 其系统是 dX(t)=2Xtdt+3XtdB(t) 和 显然,条件(A2)和(A3)对于任意的p≤2,q≤2都成立,则对于任意的‖φ‖,‖ψ‖≤R有 ‖2φ-2ψ‖∨‖3φ-3ψ‖≤3‖φ-ψ‖,i=1, ‖φ-φ3-ψ+ψ3‖∨‖2φ-2ψ‖≤(3R2+2)‖φ-ψ‖,i=2. 令LR=3R2+3≥3∨(3R2+2),则f,g是局部Lipschitz连续的,且局部Lipschitz系数为LR. 取p=3,q=2,对于充分小的ε>0,考虑函数 由定理1可得:



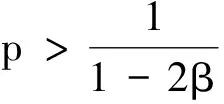

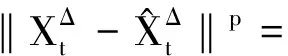

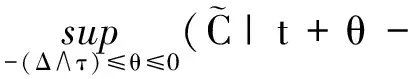






3 强收敛率分析









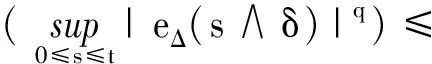

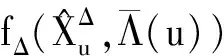
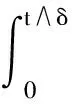
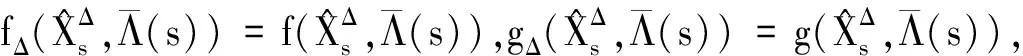
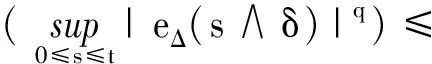

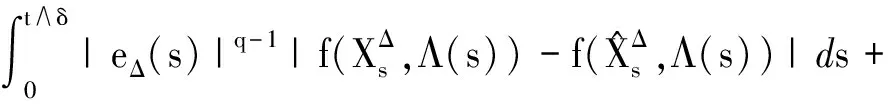

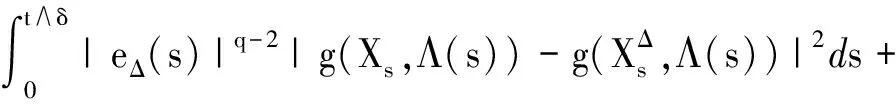

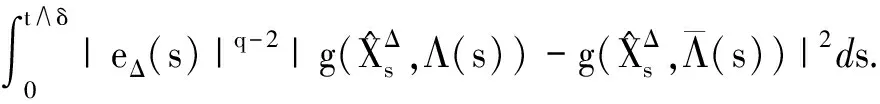





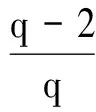



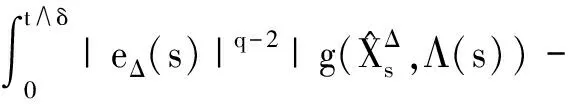
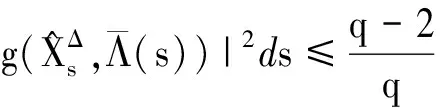
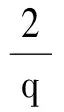
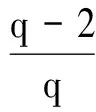

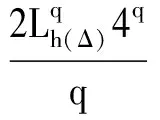
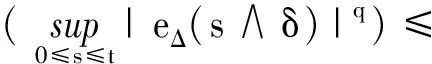
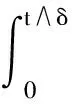
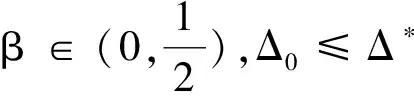
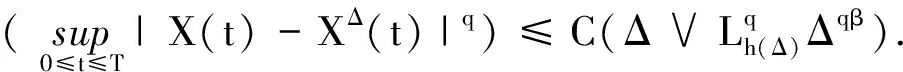


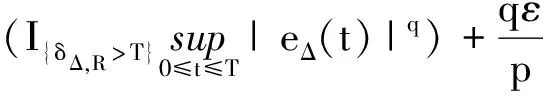

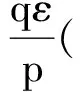




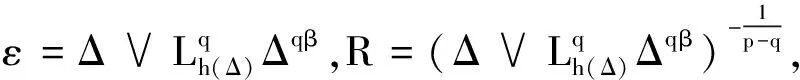

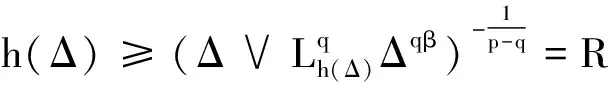
4 实例