级联模型展开与残差学习的压缩感知重构
2019-06-25熊承义李世宇高志荣金鑫
熊承义,李世宇,高志荣,金鑫
(1 中南民族大学 电子信息工程学院,武汉430074; 2中南民族大学 计算机科学学院,武汉 430074)
压缩感知理论[1]证明了:如果信号在某个域具有稀疏性,则可以由远少于奈奎斯特采样定理要求的测量值以很高的概率准确地重构该信号.压缩感知理论是一种新的信号采样理论,是对传统奈奎斯特信号采样理论的补充.压缩感知理论的提出为实现信号采样与压缩的同时完成提供了可能,也为稀疏信号的获取、处理等带来了新的选择.目前,压缩感知理论已得到广泛应用,如单像素成像、核磁共振成像、信号处理、通信与模式识别等领域[2-4].
压缩感知重构是压缩感知理论的核心问题之一,其目的在于根据压缩采样值准确恢复被采样的原始信号.压缩采样过程的数学描述可表示为y=Φx,其中x∈N是原始信号,y∈M为压缩感知测量值,Φ∈M×N称为测量矩阵.由于测量值维数M一般远小于原始信号维数N(M/N定义为采样率),因此,压缩感知重构是一个典型的病态逆问题.已知信号测量值y,传统压缩感知重构x的方法通常利用信号的稀疏性先验,通过求解式(1)的规则化优化模型实现:
(1)
其中ψ为稀疏变换矩阵,‖·‖p表示求lp范数(p∈[0,1]).式(1)中第一项称为保真项,第二项称为规则化项;λ为规则化参数,折衷重构误差与稀疏性.
由于图像信号一般具有非平稳的特性,因此利用图像的局部邻域相似,基于传统固定基(如离散余弦变换[5]、小波变换[6]、梯度变换[7]等)的稀疏表示规则化求解通常难以得到满意的重构图像质量,寻找高效稀疏表示方法成为上述优化求逆问题的关键.近年来,许多研究者鉴于图像信号普遍具有的非局部相似性,提出了图像结构组稀疏表示、低秩表示方法及其规则化重构模型[8-10],得到了更满意的重构性能.
虽然经过十多年的发展,基于上述优化模型的图像压缩感知重构已经取得了一些令人满意的结果,但是这种优化模型的求解过程往往包含大量的迭代运算,因此表现出具有很高的计算复杂度,难以满足许多实际应用的需要.此外,模型中的规则化先验(即稀疏表示)以及优化参数(如规则化参数λ等)的选取都是人工完成,具有很大的挑战性.
近年来,随着深度学习在计算机视觉领域取得成功应用,基于深度学习的图像压缩感知重构方法研究引起了广泛关注[11-13].深度学习的主要特点在于通过构建一个多层网络,并通过大量的数据样本训练网络参数,完成训练的网络根据输入可快速得到相应任务的输出.因此,与基于传统优化模型通过迭代实现的方法比较,基于深度学习的方法大大降低了图像压缩感知重构的时间复杂度.然而,基于传统神经网络的深度学习犹如一个“黑盒子”,该类方法不能有效利用图像信号的已知先验信息,因此限制了其性能的进一步提升.
鉴于基于深度神经网络的方法具有时间复杂度低的优势,但是缺乏可解释以及不能很好利用图像先验信息的不足,目前,研究者们进一步提出了基于深度展开的方法[14-17].深度展开的基本框架即是展开传统优化模型的迭代实现过程,将每一次迭代运算映射为对应的网络层,原有算法的有限次迭代运算映射为相应的多层网络,原有算法中需要人工设计的稀疏变换和优化参数通过数据样本训练确定[14].比如, MARK等人基于近似消息传递(AMP)算法提出了求解线行逆问题的学习AMP(LAMP)网络[15];YANG等人基于交替方向乘子法(ADMM)提出了磁共振图像压缩感知重构的ADMM-net网络[16];ZHANG等人基于传统迭代收缩阈值算法(ISTA)提出了自然图像压缩感知重构的ISTA-net网络[17].通过分析可以发现:虽然YANG等人提出的ADMM-net与ZHANG等人提出的ISTA-net所基于的优化模型不同,但是他们却都表现了整个网络结构本质上主要由重构层和去噪层交替多级级联而成;每一重构层生成图像的近似估计,而去噪层实现对图像近似估计中包含的噪声成分滤除.
基于深度学习理论,在一定程度上增加网络的深度,其系统的性能能够得到改善.然而,深度网络随着网络层数的增加,系统复杂度变得越来越高,网络训练也将变得更加困难.为了实现基于深度网络的图像压缩感知高质量高速重构,提出了一种模型展开优化与深度残差去噪.两级级联的深度网络结构.两级结构独立训练,降低了网络训练的难度.第一级的基于模型展开的深度网络根据输入的压缩测量值得到初始的重构图像,第二级的深度残差网络对初始重构图像进行去噪处理,最终有效提高重构质量.具体的将ADMM-Net与ResNet级联实现对磁共振图像(MRI)重构,与ADMM-Net算法相比,本文方法可提高平均峰值信噪比约0.5-0.8dB.将ISTA-Net+与ResNet级联实现对自然图像重构,在较低采样率下与ISTA-Net+算法相比,本文方法可提高平均峰值信噪比约0.6dB.
1 相关工作
当前压缩感知重构方法总体可以分为两类:一是传统的基于优化理论发展的基于模型的方法,另一是近年基于深度学习理论发展的基于网络的方法.基于模型的方法利用图像的先验信息迭代优化求解,可得到较好的重构性能,但是存在计算复杂的缺点;基于网络的方法通过样本训练得到端对端的实现,具有加速计算的优点.本节对此两类方法的典型工作分别作简要介绍.
1.1 基于模型的方法
压缩感知重构旨在由降维的测量值重建原信号根据压缩感知理论:已知测量值y,信号x的压缩感知重构的数学模型可表示为式(1).式(1)表示的逆问题求解,早期提出有凸规划方法[18].由于凸规划方法在处理高维图像信号时计算复杂度极高,因此具有相对低计算成本的各种迭代算法在后来被相继提出,如:匹配追踪(MP)算法[19]、正交匹配追踪(OMP)算法[20]、压缩采样正交匹配追踪(CS-OMP)算法[21]、迭代硬阈值(IHT)算法[22]、迭代软阈值(IST)算法[23]、近似消息传递(AMP)算法[24]、交替方向乘子法(ADMM)[25]等.
迭代(软/硬)阈值算法通过交替进行式(2a)和(2b)表示的残差生成和收缩/阈值过程,多步重复得到收敛的重构结果:
zt=y-Φxt,
(2a)
xt+1=ητ(ΦHzt+xt) ,
(2b)
其中ητ(·)为非线性收缩阈值函数,τ为设置的阈值,xt和zt分别代表第t步迭代生成的原信号x的估计以及残差y-Φxt.上标H和t分别代表共轭转置运算和迭代次数当ητ(y)=(|y|-τ)•sign(y)时,算法称为迭代软阈值(IST)方法.
近似消息传递(AMP)算法修改迭代阈值算法中的残差项为Onsager校正项,重写式(2a)为(2a')
zt=y-Φxt+zt-1η'τ(ΦHzt-1+xt-1)/δ,
(2a')
其中η'τ表示ητ的导数,δ=M/N为测量比率.
交替方向乘子法(ADMM)通过引入辅助变量,将一个复杂的优化目标分解为多个简单的目标交替优化基于ADMM的压缩感知重构首先将式(1)重写为式(3)的优化模型:
(3)
式(3)等价表示为式(4)
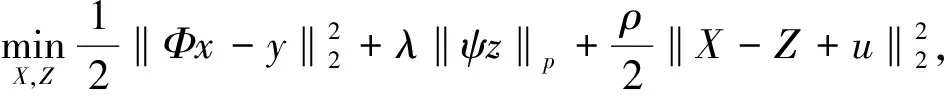
(4)
其中u是拉格朗日乘子,于是,压缩感知重构通过重复交替执行式(5a)-(5c)的计算实现:
(5a)

(5b)
ut+1=ut+Xt+1-Zt+1,
(5c)
其中,式(5a)可通过对v=Zt-ut进行阈值收缩去噪求解(p=1对应软阈值收缩,p=0对应硬阈值收缩);式(5b)表示的是求最小平方差的问题,可求助共轭梯度下降法有效求解.
1.2 基于网络的方法
基于网络的重构方法的提出,受到深度学习在计算机视觉任务成功应用的鼓舞.MOUSAVI等人最早提出了基于堆栈去噪自编码器(SDA)的CS重构网络[11];LIAIDS等人提出了基于全连接神经网络的图像和视频的CS重构网络[12];KULKANI等人进一步提出了基于卷积神经网络的CS重构网络ReconNet[13].基于网络的重构方法利用大量样本训练出一个端对端的非迭代映射,其最大优点是重构时间得到极大减少,能更好地满足实时应用的需要.
MARK等人展开近似消息传递算法,构造了求解稀疏线性逆问题的Learned AMP(LAMP)网络.LAMP网络将基于软阈值收缩的AMP迭代算法展开构成前向神经网络,而其中的最小均方误差(MSE)参数优化采用变形的反向传播(BP)算法学习.YANG等人将公式(5)中的交替方向乘子法(ADMM)的求解过程展开到网络中,提出了磁共振图像压缩感知重构的ADMM-Net网络如图1所示,ADMM-Net首先利用傅里叶逆变换获得初始重构图像x(1),然后利用卷积层c(i)代替稀疏变换矩阵ψ对x(i-1)进行稀疏变换,然后将当前x,u,c输入到非线性变换层z(i)中进行阈值收缩,再将当前x,z输入到联合更新层u(i)中对其进行更新,最后利用已经更新的z,u对重构层x(i)进行更新,如此多次交替求解.其中,每一个阶段的交替更新相当于模型优化方法中的一次迭代,即以m个阶段的网络训练完成对图像的m次迭代优化,当训练误差收敛时保存当前最优权重,作为图像快速重构模型.ADMM-Net通过L-BFGS算法对参数进行端对端的训练,并利用随机梯度下降法对网络进行优化.与ADMM-Net类似,ZHANG等人将公式(2)中迭代软阈值收缩算法(ISTA)展开到卷积神经网络中,通过多层卷积层与非线性变换处理实现对图像的软阈值去噪,提出了自然图像压缩感知重构的ISTA-net网络.

图1 ADMM-Net结构Fig.1 The architecture of ADMM-Net
2 提出的方法
基于深度学习理论,在一定程度上增加网络的深度,其系统的性能能够得到改善.然而,随着网络层数的增加,深度网络的训练也将变得更加困难.本节提出的模型展开与残差学习级联的网络,实现了在限制网络深度的条件下得到了高质量的重构图像.提出的网络结构框图如图2所示.第一级的模型展开网络用于获得较好的初始重构图像,第二级的残差学习网络对初始重构图像进行深度去噪处理,从而最终获得高质量的重构图像.整个网络的训练分步进行,训练过程相对简单且容易实现.

图2 提出的网络结构框图Fig.2 The block diagram of the proposed network
模型展开网络是根据传统优化模型,将原有迭代运算映射为相应网络层面向不同应用,采用不同优化算法可得到不同的展开网络结构.比如,针对核磁共振图像压缩感知,YANG等人[16]提出了基于交替方向乘子法(ADMM)的ADMM-net网络;针对自然图像压缩成像,ZHANG等人[17]提出了基于传统迭代收缩阈值算法(ISTA)的ISTA-net网络.
残差学习网络是根据输入的含噪声图像,利用深度残差网络提取图像包含的噪声.将输入的含噪声图像减除深度残差学习得到的噪声信号,从而重建出干净的图像信号.比起直接学习出干净图像,深度残差学习能够较好地解决深度网络的学习困难,提高网络学习的稳定性和收敛性[26].为了降低系统的复杂度,本文采用较少层的残差网络,网络深度远小于去噪网络DnCNN[27]的深度,更有利于降低网络训练的难度.考虑到压缩感知重构图像中残存的噪声为混合噪声,本文在激活函数的选择上选用LReLU(Leaky Rectified Linear Units)代替ReLU(Rectified Linear Units),增强了网络的非线性处理能力.设计的残差学习网络由一些卷积核尺寸为3×3的卷积层组成,如图3所示.每一层由三种操作的特定组合组成:卷积(Conv,Convolution),非线性变换(LReLU),批量正则化(BN,Batch Normalization)具体来说,第一层为“Conv+LReLU”,中间层为“Conv+BN+LReLU”,最后一层为“Conv”.在每一次卷积操作后,都以零填充的方式保证特征图的尺寸与原图像尺寸一致.初始重构图像(含噪图像)经残差网络处理后,可以学习其所包含的噪声图像,即残差图.用初始重构图像减除残差图,从而得到去噪后的最终重构图像.
系统的性能和复杂度主要受残差网络中间层的多少影响.鉴于自然图像种类丰富,结构相对复杂,导致其噪声去除更加困难,因此,在处理磁共振图像时设计残差网络的中间层数量比起处理自然图像时可选择更少.后面的实验表明,前者在选取中间层数量n=7,后者在选取n=11能得到较好的效果.实验也验证了,在LReLU的斜率取0.5左右时也更有利于得到好的重构结果.

图3 本文残差学习网络结构Fig.3 The architecture of proposedresidual learning network
3 网络训练
3.1 训练数据生成
对于核磁共振图像压缩感知重构,本文训练集是从脑肿瘤分子数据库(The Repository of Molecular Brain Neoplasia Data,REMBRANDT)中随机选取的110幅尺寸为256×256的脑部MRI,主要包含正面、侧面和背面三种类型的人脑MRI;对于自然图像压缩感知重构,本文所用的训练集是从ImageNet12数据集中随机选取的400张尺寸为256×256的自然图像,主要包含人物、动物、植物、风景和建筑等几种类型.首先将训练集数据输入到模型展开网络中进行训练,获得初始重构图像;然后将原图与初始重构图像进行重叠分块处理,分块尺寸为32×32,步进值为16;最后将所有图像块分为多个批次作为残差学习网络的输入数据集,每个批次包含128幅随机抽取的图像块.
3.2 训练策略
由于本文网络是包含模型展开网络和残差学习网络的一个深度网络,若对其进行整体训练,将会增加网络训练难度,无法快速获得较好的训练结果.因此,本文采取两级结构独立训练的方法,降低了网络训练的难度.先对模型展开网络进行训练,获得初始重构图像;然后将初始重构图像作为输入,对残差学习网络进行训练,获得去噪后的图像.这种分步训练的方法,每次只需对一个较浅的网络进行训练,极大的降低了系统复杂度.
3.3 损失函数
本文将真实图像x与下采样数据y成对输入,并选择最小均方误差(NMSE)作为网络训练的损失函数,通过反向传播算法修正E(θ)中各层参数θ=(W,B),得到最佳映射模型其公式如下.
(6)
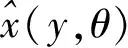
4 实验结果
实验平台为Matlab2017a,硬件条件为Intel(R)Xeon(R)CPU E5-2683,频率为2.0GHz,内存为128GB,NVIDIA TITAN X显卡,显存12GB,操作系统为Windows 10,深度学习框架为MatConvNet1.0-beta24.
对于核磁共振图像压缩感知重构,本文所用的测试集为55幅脑部MRI,在不同采样率下与傅里叶变换(FT)、全变差(TV)算法[28]、基于BM3D去噪的D-AMP[29]、和ADMM-Net[16]等算法进行对比.每个算法包含大量参数设置与自适应调整过程.在测试过程中所使用的算法参数都是原作者在相应论文中给出的最佳参数设置.从表1可知,采样率从0.05到0.5,本文算法与ADMM-Net相比平均PSNR分别提高0.87dB,0.85dB,0.67dB,0.47dB,0.51dB,0.61dB,特别是当采样率低于0.2时,本文算法的重构效果提升更加明显 .

表1 不同采样率下磁共振图像重构的平均PSNR对比(dB)Tab.1 Mean PSNR comparison of MRI reconstruction under different sampling rates
为了比较不同重构算法的主观视觉效果,本文给出了0.05采样率下脑部图像的重构图像局部两倍放大对比图,如图4和图5所示.根据结果可知,本文算法重构图像的结构纹理更加清晰.

图4 0.05采样率下Brain1重构Fig.4 Reconstructed Brain1 using 0.05 samples

图5 0.05采样率下Brain2重构Fig.5 Reconstructed Brain2 using 0.05 samples
对于自然图像压缩感知重构,本文所用测试集为自然图像压缩感知中常用的测试图像(其中leaves、monarch、lena的尺寸为256×256,peppers、fingerprint、milkdrop的尺寸为512×512).在不同采样率下将本文算法与小波变换(DCT)[5]、多假设(MH)[30]、全变差(TV)算法[28]、和ISTA-Net+[17]等算法进行对比.从表2中可知,采样率从0.04到0.20本文算法与ISTA-Net+分别提升约0.62dB、0.36dB、0.25dB和0.21dB,且在较低采样率下本文算法性能更加突出.
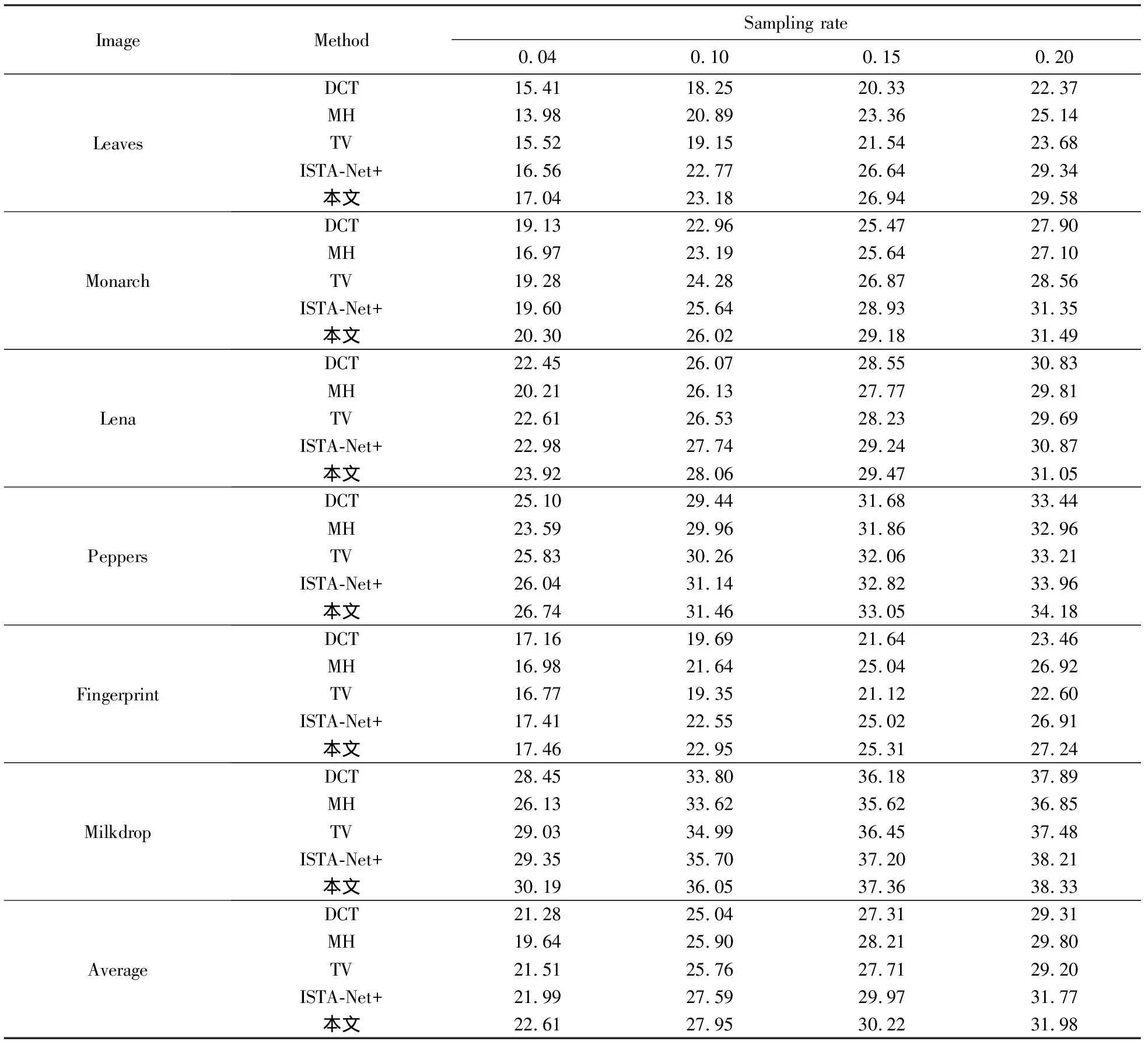
表2 不同采样率下自然图像重构PSNR对比(dB)Tab.2 PSNR comparison of natural image reconstruction under different sampling rates
为了比较不同重构算法的主观视觉效果,本文给出了leaves和lena图像在采样率为0.1下的重构图像局部两倍放大对比图,如图6和图7所示.根据结果可知,本文算法的重构图像的细节保留的更加完整.
为说明本文算法重构性能和运算效率上都具有一定优势,图8给出了55幅磁共振图像在0.05采样率下不同算法的平均重构性能和重构时间对比.由图8可以,基于稀疏变换的方法(DWT,FT)虽然可以快速获得重构图像,但是,其重构质量较差;基于模型优化的方法(MH、DAMP、和TV)的图像重构质量较好,同时其运算时间也较长;本文算法可以使用较短的运行时间,获得更好的重构效果,即其综合性能更好.

图6 0.1采样率下Leaves重构Fig.6 Reconstructed Leaves using 0.1 samples

图7 0.1采样率下Lena重构Fig.7 Reconstructed Lena using 0.1 samples
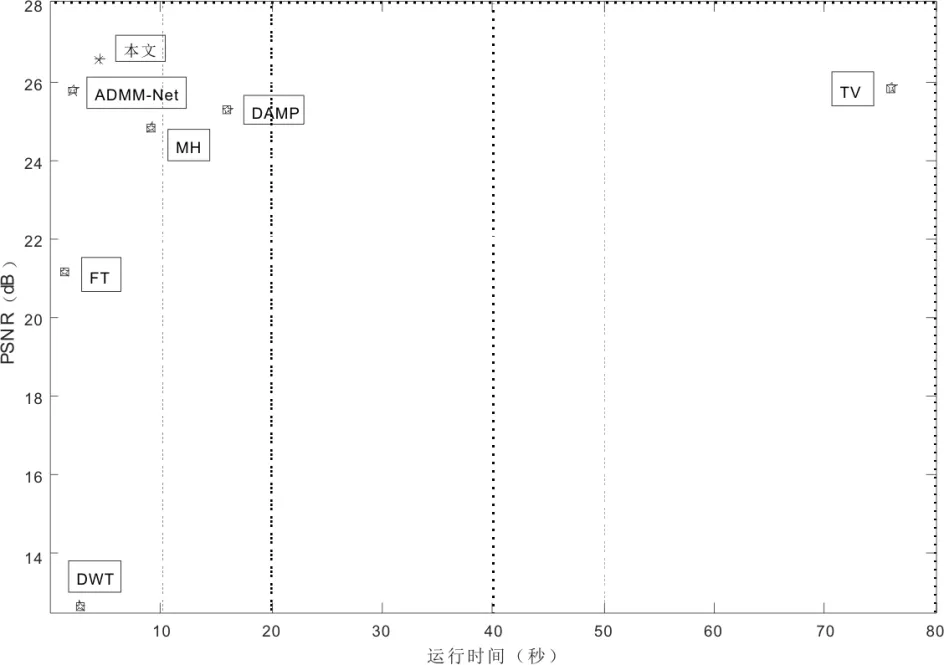
图8 0.05采样率下重构性能对比Fig.8 Reconfiguration performance comparison using 0.05 samples
5 结语
针对图像压缩感知重构问题,提出一种级联模型展开与残差学习的图像压缩感知重构算法.将模型优化方法可解释性强的优点和残差网络自学习去噪的优点相结合,实现对压缩感知图像的高质量高速重构.并通过两级网络独立训练的方法,有效避免网络加深造成的训练困难问题.大量实验结果表明,本文算法可以快速获得更高质量的重构图像,特别是在较低采样率下,重构性能更加突出.下一步工作将从图像非局部相似性先验信息入手,设计一种可解释性更强的CS重构网络.
