W型、N型反应装甲对聚能射流干扰性能研究

吕竹文，吴 越，付建平，任 凯

(1.中北大学 机电工程学院，山西 太原 030051；2.中北大学 地下目标毁伤技术国防重点学科实验室，山西 太原 030051)

聚能射流的侵彻能力很强[1]，是目前对主战坦克最具威胁性的侵彻体。因此，多年来装甲设计者希望找到能够使射流侵彻能力降低的防护手段。目前，在装甲防护中采用较多的防护手段是在装甲表面增加其他结构(如反应装甲和复合装甲等)，即所谓的附加装甲[1]。这些附加装甲能够使射流减速、侵蚀、破碎和偏转等[2]，从而降低射流侵彻能力。

最典型的附加装甲有主动反应装甲、被动反应装甲和复合装甲等。主动反应装甲通过驱动金属板与射流直接碰撞(爆炸反应装甲)或在距离装甲车辆一定距离处碰撞(主动装甲或电磁驱动装甲)，来降低射流侵彻能力，达到防护的目的。被动反应装甲和复合装甲主要采用高强度材料和特殊的几何设计来对付聚能射流侵彻。

爆炸反应装甲由两层相对较薄的钢板和一层夹层炸药组成(称作“三明治”结构)[3]。通常情况下，在主战坦克装甲上布置不止一层反应装甲盒，但是如果在一个反应装甲盒内，有3层“三明治”单元，就可以提高单个反应装甲盒抗击射流的能力。当聚能射流的入射角度分别为45°、90°时，使用ANSYS/LS-DYNA前处理建立聚能射流侵彻W型、N型3层爆炸反应装甲模型，通过数值模拟，对比分析两种布置方式对聚能射流的干扰能力，为多层爆炸反应装甲组合优化提供一定的参考。

1 构建数值模拟模型

在双层爆炸反应装甲中，通常有两种布置方式，即平行反应装甲和楔形反应装甲。文献[4]得出结论：双层平行反应装甲干扰射流效率高于楔形反应装甲，但是在实际应用过程中，双层平行反应装甲存在一个致命的缺陷，就是当聚能射流与反应装甲垂直作用时，反应装甲的干扰能力会急剧下降，而双层楔形反应装甲则不存在这一问题。在此基础上，设计了W型、N型3层爆炸反应装甲组合。文献[4]指出对于双层爆炸反应装甲，其干扰能力还与上下两层爆炸反应装甲的夹角有关，并通过数值模拟得出结论：在夹角<14°时，随着夹角的增大，射流的侵彻能力呈下降趋势，但在两组件夹角>19°后，反应装甲夹角变化对残余射流的侵彻深度影响并不敏感。因此，在文中的数值模拟模型中，3层反应装甲的组件之间的夹角为15°；在W型、N型3层爆炸反应装甲的组合中，基本组件采用2/4/2结构[5]。W型爆炸反应装甲布置方式如图1所示。

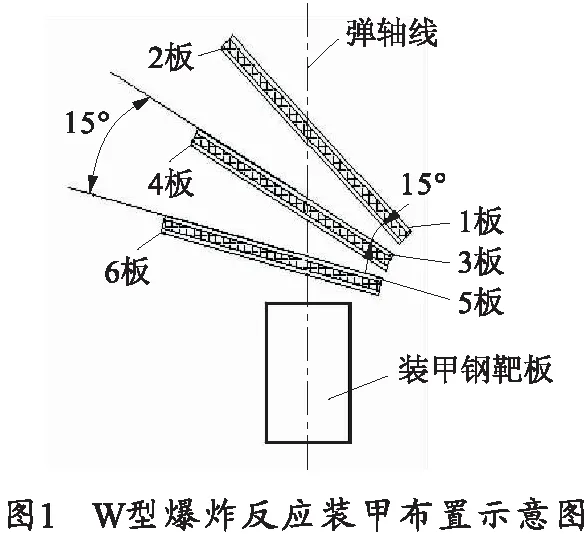
1.1 基本假设

聚能射流与爆炸反应装甲作用的过程十分复杂[6]，涉及到射流引爆夹层炸药、炸药爆轰、炸药的爆轰波干扰射流以及飞板的碰撞运动[7]，而笔者主要是对W型、N型3层爆炸反应装甲对射流的干扰性能进行研究，做如下假设：

1)聚能射流瞬时引爆夹层炸药。

2)由于炸药爆轰后产生的压力远远大于飞板所受的重力和空气阻力，所以只考虑爆轰压力。

3)爆炸反应装甲被引爆后，上层反应装甲的背板和下层反应装甲的面板发生完全塑性碰撞，且碰撞瞬时完成，共同飞离弹轴线。

1.2 构建有限元模型

该数值模型为轴对称结构，为方便计算，建立二分之一模型。利用ANSYS/LS-DYNA进行三维建模，数值模型采用g-mm-μs单位制。数值模型由主装药、药型罩、空气、爆炸反应装甲、装甲钢靶板等部分组成，其中空气、主装药以及药型罩3个单元使用欧拉网格进行建模[8]；爆炸反应装甲以及装甲钢靶板单元使用拉格朗日网格进行建模，并且在靶板单元与空气单元、主装药单元、药型罩单元之间采用ALE算法[9]。通过在ANSYS/LS-DYNA的K文件中使用*CONSTRAINED_LA-GRANGE_IN_SOLID关键字实现固体与流体间的耦合。

在数值模拟中，采用直径为56 mm、高为50 mm标准聚能装药，其中，药型罩的壁厚为1 mm，药型罩锥角为60°，起爆方式为炸药顶端起爆[10]。爆炸反应装甲的面板、背板厚2 mm，炸药层厚4 mm.为了能够更好地观察W型、N型爆炸反应装甲对聚能射流的干扰能力，在下层反应装甲下方40 mm处布置长为40 mm、宽为20 mm、高为60 mm的装甲钢靶板。图2为聚能射流与W型、N型爆炸反应装甲作用的有限元模型。

1.3 本构模型和状态方程

主装药类型为8701炸药[8]，材料模型为高能炸药爆轰模型，状态方程为JWL状态方程，其基本形式为

p=Fpeos(V,E)，

(1)

(2)

式中：p为任意时刻炸药单元释放的压力；peos为JWL状态方程的炸药爆轰产物压力；F为炸药燃烧质量分数；V为相对体积；E为单位体积的内能密度；A、B、R1、R2和w为输入参数。

表1为8701炸药的本构模型参数。药型罩材料为紫铜，采用Steinberg材料模型和Gruneisen状态方程来描述，材料参数如表2、3所示。整个数值模拟过程，限定在一个空气域内，空气域的参数如表4所示。

表1 8701炸药本构模型参数[1]

表2 紫铜药型罩Steinberg材料模型参数[1]

表3 紫铜药型罩Gruneisen状态方程[1]

表4 空气域材料参数[1]

2 数值模拟结果及分析

2.1 入射角不同，聚能射流侵彻不同布置的反应装甲

当入射角为45°时，聚能射流与W型、N型爆炸反应装甲作用过程如图3、4所示。

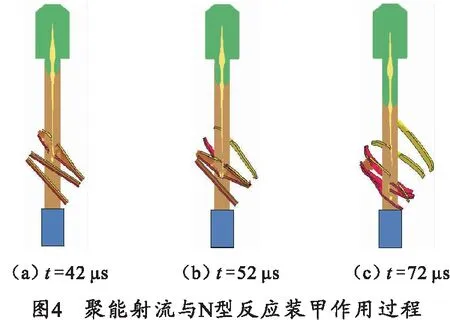
图3、4中，在t= 0 μs时设置炸药起爆，炸药爆轰后开始压垮药型罩形成射流，射流逐渐拉伸，射流头部到达上层反应装甲后开始侵彻，引爆夹层炸药，在t=42 μs时与上层反应装甲作用完毕，如图3、4中(a)所示，射流在与上层反应装甲作用后，射流的头部变粗，且出现断裂；在t=52 μs时，射流与中间层反应装甲作用完毕，射流头部分裂成两部分，且射流因接连与两层反应装甲作用，射流已经出现拉长、断裂的现象；从图4(c)中可以看出，在与第3层反应装甲作用后，射流头部已经断裂为3部分，而且射流已经开始偏离弹轴线。聚能射流以这种不连续的状态侵彻装甲钢靶板，侵彻能力自然会下降。

当入射角为90°时，聚能射流垂直侵彻W型、N型爆炸反应装甲作用过程如图5、6所示。

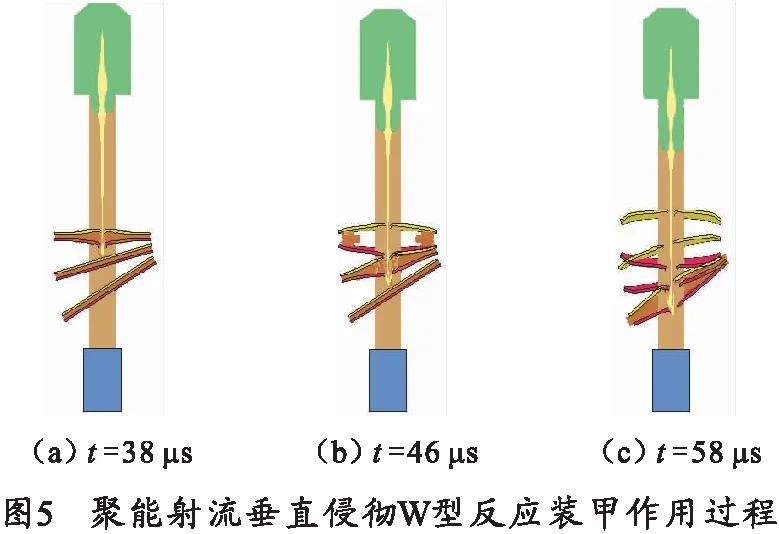
如图5(a)、图6(a)中所示，当聚能射流在垂直侵彻W型、N型反应装甲的第1层后，射流头部出现断裂；在t=46 μs时出现不同，射流在与中间层反应装甲作用后，在图5(b)中，射流头部还是处于断裂状态，但在图6(b)中，后续射流已经增补上；在t=58 μs时，射流头部穿过第3层反应装甲，且未出现射流断裂、偏离弹轴线的情况。

2.2 射流速度对比分析

聚能射流在与上层爆炸反应装甲作用后，它的侵彻速度开始降低，紧接着与中间层、下层反应装甲作用，以这种低速状态，很容易出现射流断裂，当遇到装甲钢靶板时，会再次出现速度衰减，这样聚能射流的侵彻能力便会大幅度下降。射流的入射角度分别为45°、90°时，与W型、N型反应装甲作用的速度曲线如图7所示。

从图7中可以看出，入射角度为45°时，聚能射流与W型反应装甲作用后的剩余速度是4条曲线中最低的；聚能射流与N型反应装甲作用后，在t=120 μs时，出现速度急剧降低，但是经过大约20 μs后，后续射流增补上后，速度逐渐回升，继续侵彻过程；当聚能射流垂直侵彻W型、N型反应装甲时，射流速度下降的值小于入射角度为45°时，且射流仍具有较高的侵彻能力，继续侵彻装甲钢靶板。

2.3 射流侵彻靶板对比分析

入射角度为45°和90°时，聚能射流与W型、N型反应装甲作用后，侵彻装甲钢靶板后效图如图8所示，其侵彻孔径与侵彻深度数值如表5所示。

表5 射流侵彻靶板的相关参数

参数入射角度为45°W型N型入射角度为90°W型N型侵彻孔径/mm31302322侵彻深度/mm1963360

由图8和表5可以得出，当入射角度为45°时，聚能射流在与W型、N型反应装甲作用后，射流开始偏离弹轴线，因此在侵彻装甲钢靶板时，侵彻孔径较大，但此时射流的侵彻能力已经较低，因此开孔能力较差；与N型反应装甲作用后的聚能射流的侵彻能力明显低于与W型反应装甲作用后的，这是因为N型反应装甲的上、下层反应装甲呈平行布置，当非垂直侵彻双层反应装甲时，双层平行反应装甲干扰射流效率高于楔形反应装甲，这与文献[4]中得出的结论是相同的；当聚能射流垂直侵彻W型、N型反应装甲后，聚能射流并未出现偏离弹轴线的情况，因此孔径的直径较小，但是射流仍具有较高的侵彻能力，侵彻深度大大提高，尤其是与N型反应装甲作用后，聚能射流贯穿装甲钢靶板。在实际应用过程中，双层平行反应装甲存在一个致命的缺陷，就是当射流与反应装甲垂直作用时，反应装甲的干扰能力会急剧下降，这与文献[4]中得出的结论是一致的。

3 结论

在数值模拟仿真中，当入射角度为45°、90°时，聚能射流分别与W型、N型反应装甲作用后，得出以下结论：

1)当入射角度为45°时，N型反应装甲具有最好的干预射流的能力，与W型反应装甲相比，干预射流开坑深度能力提高了3.17倍。

2)当垂直侵彻时，W型反应装甲干预射流的能力明显高于N型反应装甲，干预射流开坑深度能力提高了1.81倍。

在实际应用中，大多采用双层楔形反应装甲，由于可能出现任意角度的侵彻，对于双层平行反应装甲干预射流的良好能力不应放弃。W型反应装甲的缺点是会增加反应装甲盒的体积，但是当射流垂直侵彻时，仍具有较好的干预射流的能力；N型反应装甲不会使反应装甲盒的体积增加较大，但是N型反应装甲在面对垂直侵彻时，它的干预能力会大幅度下降，根据文中的数值模拟仿真结果，给出的建议是：把平行反应装甲盒与楔形反应装甲盒组合起来使用，同时协调体积与质量问题，避免给坦克增加不必要的负载，这样反应装甲盒可以面对多角度的聚能射流。