电磁轨道发射器数值模拟与速度测量

贺景瑞，李小将，万 敏

(航天工程大学 宇航科学与技术系，北京 101416)

电磁轨道发射器是一种利用电能取代传统化学能的新型发射器，在导弹防御、舰载火炮和导弹弹射等方面具有应用潜力[1-4]。当前，美国海军的电磁轨道发射技术正逐渐从实验室走向军事化应用[5]，其测试的电磁轨道发射器能推动炮弹以2 km/s以上的速度射出，并且击穿160 km以外的混凝土。美国海军将在此基础上推进发射速率为10发/min的长寿命发射器的研制工作。我国对电磁轨道发射器的研究仍处于关键技术验证阶段[6]。

为准确模拟电磁轨道发射器的电磁过程并预测其性能，研究人员在数值模拟方面进行了大量研究。文献[7-9]采用矢量磁位和标量电位描述的电磁场扩散方程建立了三维瞬态电磁场计算模型，利用有限元/边界元耦合方法进行求解，计算了电枢运动过程、电磁场和温度。文献[10]基于磁扩散方程、安倍定律和实验数据，通过有限元计算求得考察点磁场和电场特性。文献[11-16]以磁通密度Bz为自变量，建立了轨道和电枢内的二维磁扩散模型。文献[17-19]基于触发策略自动计算方法，建立了电磁轨道发射器电路模型，能够求解电枢的运动过程。

笔者考虑摩擦力、空气阻力的影响，基于磁扩散方程、热传导方程和运动学方程建立电磁轨道发射器的计算模型。针对矩形电枢普通发射器、C形电枢普通发射器和增强型发射器进行数值模拟，分析其电磁场、温度场和运动学特性。结合电磁发射试验中的测量数据，对计算模型进行了验证。

1 电磁轨道发射器控制方程

1.1 电磁场控制方程

根据麦克斯韦方程结合欧姆定律及本构方程，得磁场扩散方程[20]:

(1)

式中：B为磁通密度；μ为材料磁导率；σ为电导率；v为电枢相对轨道的运动速度；t为时间。

为简化计算，采用固定电枢，轨道相对电枢运动的方式进行等效替换，轨道速度为负值。将式(1)简化为二维磁扩散方程，推得轨道中的磁扩散方程为

(2)

电枢中的磁扩散方程为

(3)

电磁轨道发射器的二维求解模型如图1所示。

电磁场边界条件设置如下。

1.1.1 第1种边界条件

电枢后端边界S5，轨道内侧边界S4、S7设为Dirichlet边界条件，具体表达式根据发射器结构不同而不同，确定边界条件如下。

1.1.1.1 矩形电枢普通发射器

根据磁场叠加原理对轨道进行分析，轨道内侧磁通密度由轨道内电流产生的磁通密度和另一轨道在其表面激发的磁通密度两部分组成。因此，轨道内表面的磁通密度BPR可表示为

(4)

式中：I为电流；h为轨道高度；r为轨道间距；w为轨道宽度。

根据安培环路定律，通过电枢的电流产生的磁通密度为

(5)

式中，la为矩形电枢长度。

根据毕奥-萨伐尔定律，轨道在电枢上激发的磁通密度为

(6)

因此，普通型电磁轨道发射器电枢后部磁通密度为

BPA=BPA00+BPAR0.

(7)

1.1.1.2 C形电枢普通发射器

C形电枢头部后侧磁通密度由流过电枢和流过轨道的电流共同产生。C形电枢头部后表面的磁通密度可表示为

(8)

式中：ha为电枢高度；ra为电枢头部半径。

1.1.1.3 C形电枢增强型发射器

增强型电磁轨道发射器采用在主轨道外侧串联一对副轨道的方式来增强磁场，其结构如图2所示。

增强型电磁轨道发射器轨道内表面的磁通密度由流过轨道电流产生的磁通密度和其他轨道产生的磁通密度叠加而成，表示为

(9)

电枢头部后侧表面的磁通密度由电枢电流产生的磁通密度和轨道产生的磁通密度叠加而成，表示为

(10)

1.1.2 第2种边界条件

电枢前端边界S6，轨道前端边界S3、S9、S11、S12和轨道外侧边界S2、S10设为Dirichlet边界条件B=0.

1.1.3 第3种边界条件

根据磁扩散方程得到发射器内每一点的磁通密度后，可由安培定律推得发射器内电流密度表达式：

(11)

1.2 温度场控制方程

发射过程中发射器产生的焦耳热可表示为

(12)

根据热传导方程结合式(12)，得发射器二维热传导方程：

(13)

式中：T为温度；ρ为材料密度；cp为材料比热容；k为材料热导率。

温度场中求解域的边界条件为：

2)初始时刻T(x,y)|t=0=300 K.

1.3 电枢运动方程

电枢在轨道内运动时，在轴向受到电磁推力F作用向前运动，电枢向前运动的同时压缩前方空气，受到滑动摩擦力fd和空气阻力fk.

电枢受到的电磁推力由洛伦兹力公式计算：

(14)

式中：S为积分面积；dτ为微小面积元素。

电枢受到的空气阻力为

fk=1.1ρaAv2,

(15)

式中：ρa为电枢前空气的初始密度；A为电枢的横截面积；v为电枢运动速度。

电枢与轨道的摩擦力为

fd=μdFN，

(16)

式中：μd为摩擦系数；FN为电枢与轨道的接触压力。

枢轨接触面的的磨损会使电枢过盈压力下降，但是电枢温升带来的膨胀，抵消了磨损造成的尺寸变化。可近似认为电枢运动过程中过盈压力保持不变，并且忽略温度影响。因此，接触压力可由两部分表示：一是装入电枢时产生的过盈压力；另一部分是作用在电枢的电磁力带来的电枢形变与轨道间产生的压力。接触压力近似表示为

FN=F0+Fm，

(17)

式中：F0为电枢过盈压力；Fm为作用在电枢上的电磁力引起的形变带来的纵向压力。

根据实验室测量，电枢过盈压力F0取值100 N。Fm采用COMSOL Multiphysics中的固体力学模块求解。

发射器设为线弹性材料，位移场和速度场初始值设为0。在电枢两侧尾翼分别施加体载荷条件，体载荷大小为电磁场控制方程求解出的电枢电磁力垂直运动方向分力在该时刻的数值。轨道外表面设为固定约束，其他表面设为自由条件。

由牛顿第二定律得电枢加速度、速度和位移方程：

(18)

式中：a为电枢加速度；x为电枢位置。

2 电磁轨道发射器数值模拟

2.1 仿真计算模型

2.1.1 脉冲电源模型

脉冲电源模型采用Simulink中的Simscape模块建立，如图3所示。

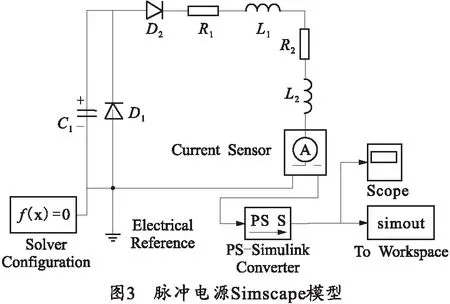
图3中，C1为储能电容，D1为续流二极管，D2为反向截止二极管，R1为除轨道外的电路总电阻，L1为除轨道外的电路总电感，R2为轨道电阻，L2为轨道电感。为便于计算，固定轨道电阻和电感，不随电枢运动改变。储能电容设为8 mF，输出电流曲线如图4所示。

2.1.2 电磁场和温度场有限元模型

在COMSOL Multiphysics中分别建立矩形电枢普通发射器、C形电枢普通发射器和C形电枢增强发射器的几何模型,如图5所示。

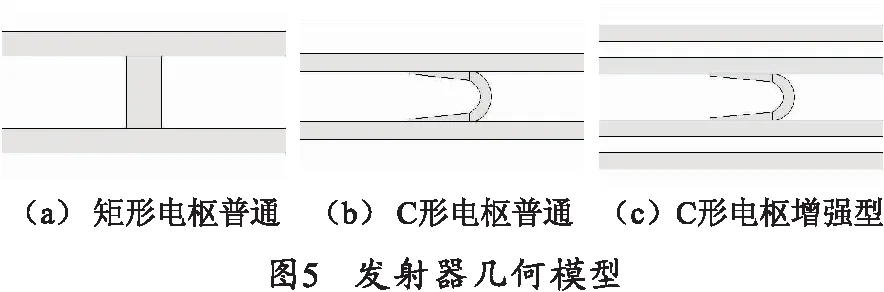
轨道长度为1 000 mm，宽度为7 mm，高度为20 mm，轨道材料采用铜。矩形电枢长度为110 mm，宽度为20 mm，高度为20 mm。C形电枢结构参数如图6所示，图中单位为毫米。所有电枢材料均采用铝。

采用COMSOL Multiphysics中的偏微分方程模块求解电磁场和温度场控制方程。按照电磁轨道发射器控制方程一节中给出的域方程和边界条件设置偏微分方程求解模块。网格划分采用自由剖分三角形网格。

2.1.3 模型求解流程

仿真计算模型使用MATLAB作为脚本编写工具设置和求解COMSOL Multiphysics有限元程序，将电磁轨道发射中的电路模型、运动学模型、电磁场模型、传热学模型集成起来，分析轨道炮发射过程中的场分布与电枢运动规律。仿真模型求解思路如图7所示。

仿真过程中，设置各项参数如表1所示。

表1 仿真计算参数

2.2 仿真计算

将轨道内侧的磁通密度和电枢后部磁通密度作为边界条件,输入电磁轨道发射器控制方程并进行求解，得到发射器的电磁场、温度场和电枢速度计算结果。

2.2.1 电磁场计算

图8为1 ms时刻矩形电枢普通发射器、C形电枢普通发射器和增强型发射器的电磁场分布图。

从图8中可以看出，在发射过程中，发射器内产生速度趋肤效应，即速度引起了磁通密度和电流在电枢和轨道接触面后部集中的现象。在使用相同脉冲电源的条件下，1 ms时刻，矩形电枢上的最大磁通密度为2.56 T，C形电枢上的最大磁通密度为3.51 T.采用C形电枢后发射器的磁通密度提升了37%.在采用C形电枢的条件下，增强型轨道发射器的最大磁通密度为4.08 T，相比普通型发射器磁通密度提升了16%.

图9为1 ms时刻矩形电枢普通发射器、C形电枢普通发射器和增强型发射器的电流密度分布图。图9中，矩形电枢普通发射器的最大电流密度为1.81×109A/m2，C形电枢普通发射器的最大电流密度为1.46×109A/m2.采用C形电枢能够明显降低发射器的最大电流密度。增强型发射器的最大电流密度为2.52×109A/m2，高于普通型发射器。这是因为在1 ms时，增强型发射器的速度为177.52 m/s，速度趋肤效应强于普通型发射器。

2.2.2 温度场计算

在电磁发射过程中，发射器会产生大量的热能，导致发射器温度瞬间升高。过高的温度会引发发射器损伤，进而影响发射效能。因此，有必要对不同类型发射器的温度变化进行分析。

图10为矩形电枢普通发射器、C形电枢普通发射器和C形电枢增强型发射器电枢出口时刻的温度分布图。矩形电枢普通发射器的高温区域出现在枢轨接触面尾部及其附近区域，最高温度为335.7 K;C形电枢普通发射器的高温区域为枢轨接触面附近和电枢喉部，最高温度为333.4 K;增强型发射器的高温区域为枢轨接触面后方、电枢尾翼和电枢喉部，最高温度出现在枢轨接触面后方，为346.9 K.

2.2.3 电枢速度计算

图11为矩形电枢普通发射器、C形电枢普通发射器和C形电枢增强型发射器电枢速度曲线。矩形电枢普通发射器的出口速度为216.9 m/s；C形电枢普通发射器的出口速度为310.7 m/s；C形电枢增强型发射器的出口速度为444.9 m/s.

电磁轨道发射器系统效率可表示为：

(19)

式中：Ek为电枢出口动能；E0为系统初始储能。

系统初始储能为

(20)

式中：C为电容值；U为电容器初始电压。

通过计算得到矩形电枢普通发射器、C形电枢普通发射器和C形电枢增强型发射器的系统效率分别为5%、11%和24%.

3 电磁轨道发射器发射试验

采用增强型电磁轨道发射器进行发射试验。发射器管身口径为20 mm×20 mm.轨道材料采用H62黄铜，轨道尺寸为1 000 mm×40 mm×7 mm.发射电流由电容储能型脉冲电源产生，发射试验参数如表2所示。

表2 发射试验参数

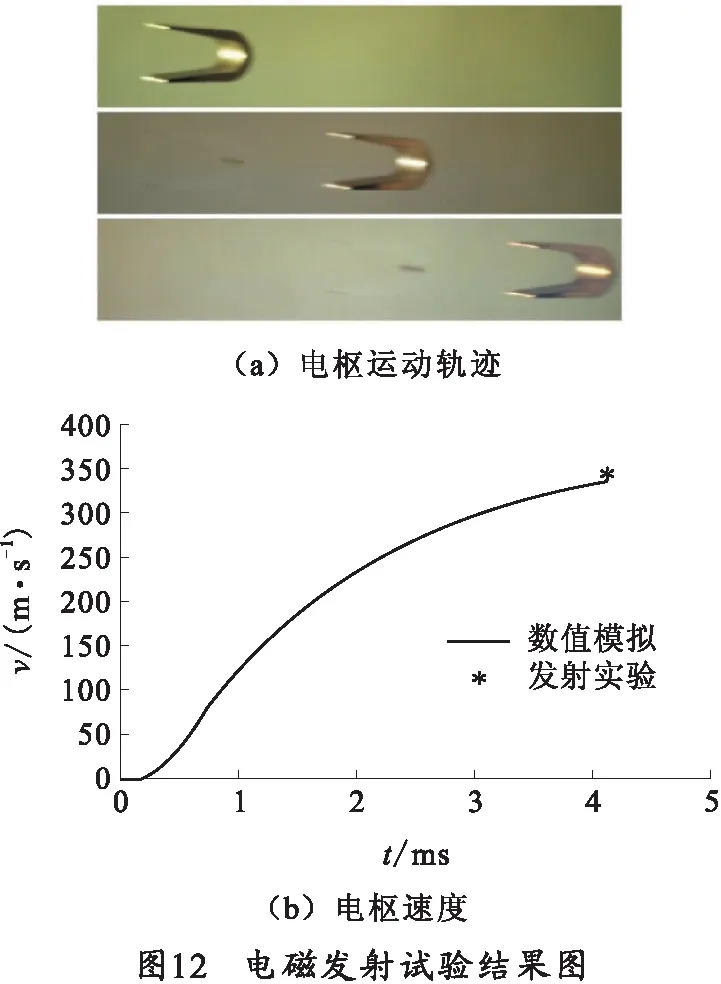
选择利用高速相机对电枢的出口速度进行测量，结果如图12所示。图12(a)为电枢运动轨迹图，测得电枢出口速度为343.23 m/s；图12(b)为电枢速度的数值模拟结果。电枢出口速度数值模拟结果为335.3 m/s，与试验结果的偏差为2.3%.数值模拟结果与试验测量结果相近，验证了本文所建模型的准确性。

4 结束语

笔者建立了基于磁扩散方程、热传导方程和运动学方程的电磁轨道发射器计算模型。根据安培环路定律和毕奥-萨伐尔定律确定了矩形电枢普通发射器、C形电枢普通发射器和增强型发射器的控制方程边界条件B，并对矩形电枢普通发射器、C形电枢普通发射器和增强型发射器进行数值模拟，得到磁场分布、电流密度分布、温度分布和电枢速度曲线。计算结果表明，C形电枢相比矩形电枢能够提升磁通密度和出口速度，并降低电流密度和温度。增强型发射器相比普通发射器能够提升磁通密度和出口速度，但其电流密度和温度因速度趋肤效应影响而上升。

在电磁发射试验中，采用增强型电磁轨道发射器进行了发射试验。利用高速相机测得电枢出口速度，数值模拟和发射试验结果基本吻合，偏差为2.3%，验证了本文计算模型的准确性。