嵌岩抗滑桩地基水平抗力系数K值取值的数值模拟研究
2019-06-24焦世杰
焦世杰
(中铁四院集团西南勘察设计有限公司,云南 昆明 650200)
抗滑桩设计中,桩身内力计算是决定设计成败的关键因素。目前,抗滑桩内力的计算有很多方法,如悬臂桩法、地基系数法、矩阵分析法、双参法、p-y曲线法、有限单元法等[1-10]。悬臂桩法出现早,计算简单,在实际工作中应用最多,该方法视滑动面以下为弹性地基梁,根据滑动面以下岩、土的地基水平抗力系数K值计算锚固段的桩壁应力以及桩身各截面的内力和位移。悬臂桩法视地基水平抗力系数K值的不同假定,分为“K”法、“m”法和“C”法[1]。其中,以弹性地基梁“K”法为基础的解析法因其具有计算模式明确、计算过程简单的优点,被广泛应用于嵌岩抗滑桩结构设计。“K”法假定抗滑桩嵌固段岩体地基水平抗力系数K值为常数,主要适用于较完整的硬质岩层、未扰动的黏土岩或性质相近的半岩质地层[11]。
“K”法中,不同K值对抗滑桩内力计算的影响较大,如果K值取值较抗滑桩嵌固段岩体的实际值大,则可能会出现抗滑桩倾覆的危险;若K值取值较嵌固段岩体的实际值小,则会增加工程造价。可见,抗滑桩嵌固段岩体地基水平抗力系数K值取值的准确与否直接影响抗滑桩工程的安全性、适用性、耐久性和经济性。在工程实践中,“K”法中抗滑桩嵌固段岩体的地基水平抗力系数K值大多是参考铁道部第二勘测设计院编写的《抗滑桩设计与计算》,根据岩石的饱和单轴抗压强度,通过查表并在一定范围值内凭经验取值,基本未考虑岩体上裂隙的发育程度与变形性质,带有较大的随意性。众所周知,抗滑桩嵌固段岩体地基水平抗力系数K值是岩体的一个变形参数,而不是岩块的强度参数,其值大小与岩体的变形参数与强度密切相关。如何根据岩体的变形特性与强度获得较准确的抗滑桩嵌固段岩体的地基水平抗力系数K值是工程领域与学术界讨论的热点与难点问题。为此,本文对嵌岩抗滑桩地基水平抗力系数K值的取值问题进行了数值模拟研究。
1 嵌岩抗滑桩的数值模拟
1.1 模型受力的假定
拟建立的数值模型的计算范围为:x方向的长度为60 m,y方向的长度为30 m,抗滑桩桩长20 m,嵌固段长10 m,桩宽1 m,如图1所示。为了使计算模型在反映真实地质条件的同时也能使计算过程更为简便,故做如下假设:由于本文主要研究抗滑桩嵌固段桩身内力和位移,为了使分析更为简单明了,仅建立滑动面以下部分模型,即将滑动面以上的滑体重量简化为作用在滑床上的均布荷载,其大小为200 kN,滑坡推力为600 kN/m,而对于滑体则不再建立有限元模型。
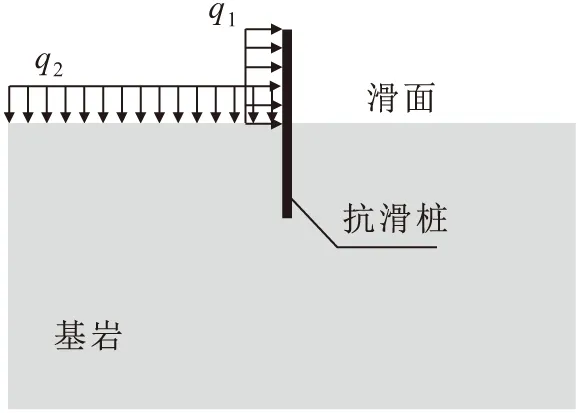
图1 抗滑桩简化模型Fig.1 Simplified model for anti-slide pile
1.2 模型计算参数
本文采用大型有限元软件ANSYS对抗滑桩嵌固段桩身内力和位移进行数值模拟,研究抗滑桩嵌固段岩体变形参数中弹性模量E和泊松比υ对抗滑桩嵌固段岩体地基水平抗力系数K值的影响。抗滑桩嵌固段岩体的力学计算参数为:内摩擦角φ为40°,容重γ为24 kN/m3,黏聚力c为200 kPa。抗滑桩采用C30混凝土,其力学计算参数为:弹性模量E为3×1010Pa,泊松比υ为0.2,容重γ为27 kN/m3。
1.3 数值模拟方案
本次数值模拟通过改变抗滑桩嵌固段岩体的变形参数来研究嵌固段岩体变形参数的变化对抗滑桩桩身内力和位移的影响,并求得抗滑桩嵌固段岩体地基水平抗力系数K值与岩体弹性模量和泊松比的函数关系,具体数值模拟方案见表1。

表1 数值模拟方案
2 有限元模拟结果与分析
针对表1中方案依次进行数值模拟,并根据数值模拟得出的抗滑桩嵌固段岩体的桩壁应力和位移,计算出各种方案的地基水平抗力系数K值。由于不同方案之间嵌固段岩体弹性模量的数量级相差较大,因此本文将嵌固段岩体弹性模量数量级分别为1×108、1×109、1×1010的方案分为第一组、第二组、第三组,模拟得到每组方案嵌固段岩体的桩壁应力和位移,见图2至图7。
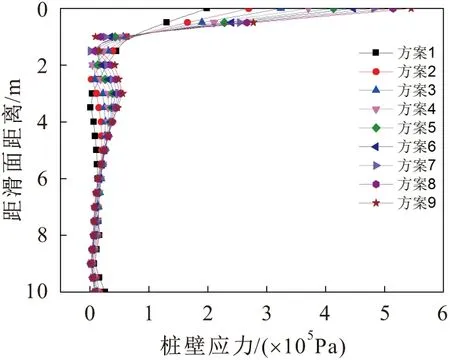
图2 第一组方案嵌固段岩体的桩壁应力图Fig.2 Stress diagram of the pile wall of rock mass embedded under the first set condition
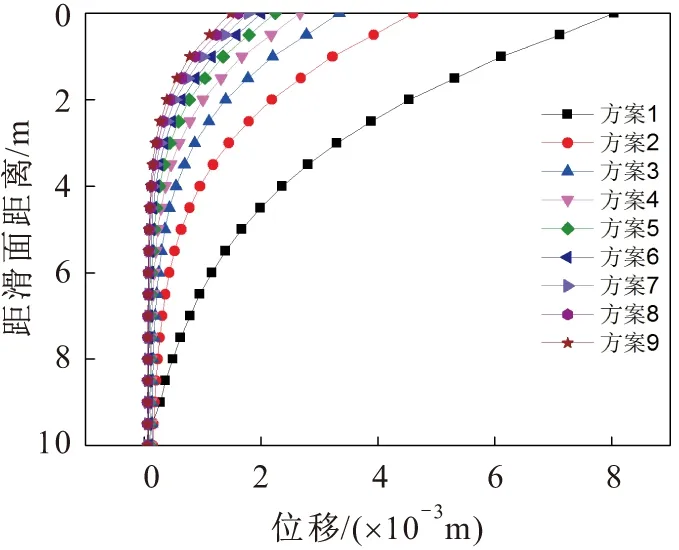
图3 第一组方案嵌固段岩体位移图Fig.3 Displacement diagram of rock mass embedded under the first set condition
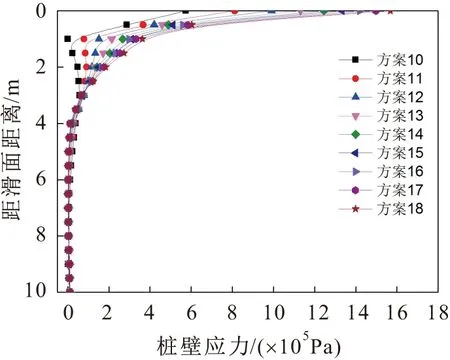
图4 第二组方案嵌固段岩体的桩壁应力图Fig.4 Stress diagram of the pile wall of rock mass embedded under the second set condition
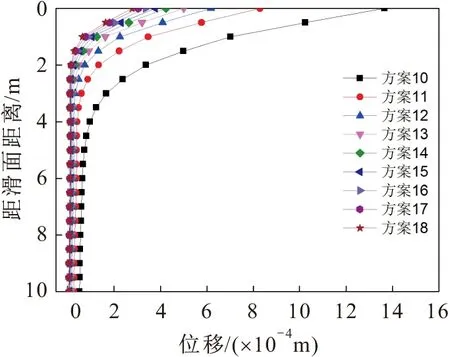
图5 第二组方案嵌固段岩体位移图Fig.5 Displacement diagram of rock mass embedded under the second set condition
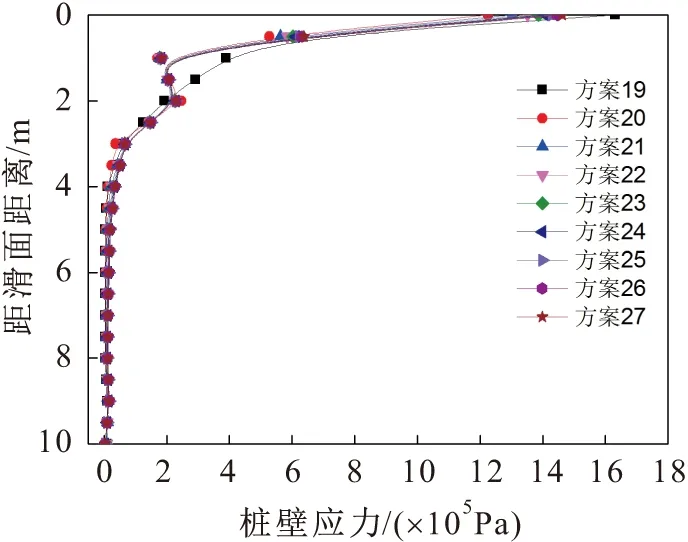
图6 第三组方案嵌固段岩体的桩壁应力图Fig.6 Stress diagram of the pile wall of rock mass embedded under the third set condition
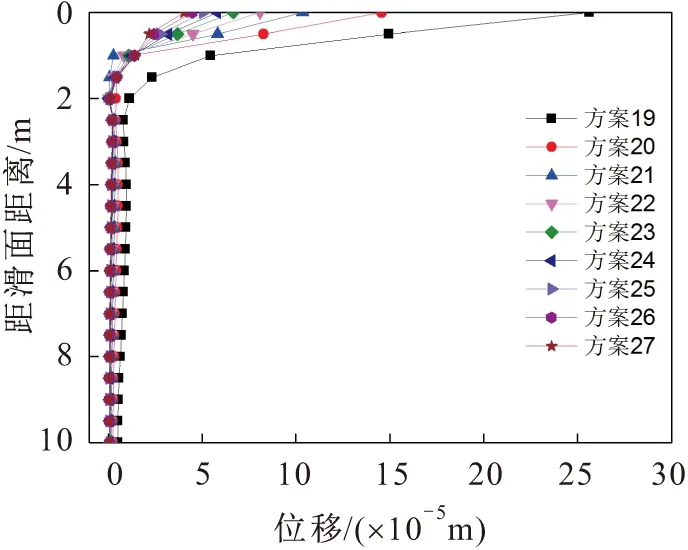
图7 第三组方案嵌固段岩体位移图Fig.7 Displacement diagram of rock mass embedded under the third set condition
由图2、图4和图6可见,嵌固段岩体的桩壁应力在滑面处最大,并且随着深度的增加逐渐减小;在同一深度内,嵌固段岩体的桩壁应力随着岩体弹性模量的增加逐渐增大,随着岩体泊松比的增加逐渐减小。
由图3、图5和图7可见,嵌固段岩体的位移在滑面处最大,并且随着深度的增加逐渐越小;在同一深度内,嵌固段岩体的位移随着岩体弹性模量的增加逐渐减小,随着岩体泊松比的减小也逐渐减小。
根据已有规范可知,抗滑桩嵌固段岩体地基水平抗力系数可以取某一深度范围内的平均值。由图2至图7可见,滑面附近一定范围内的嵌固段岩体的桩壁应力变化较大,由于滑面附近应力集中现象较明显,同时由于抗滑桩嵌固段岩体在滑面附近存在塑性变形区,因此在深度4 m以下表现不明显;另外,同时由于桩底应力集中现象较明显,经试算本文将滑面以下4~8 m深度内嵌固段岩体地基水平抗力系数的平均值作为该组嵌固段岩体地基水平抗力系数,其与该组数值模拟得到的嵌固段岩体桩壁应力和位移的结果最为接近。由于嵌固段岩体地基水平抗力系数K值为桩壁应力与位移的比值,因此可得到各种方案的嵌固段岩体地基水平抗力系数K值的取值见表2。
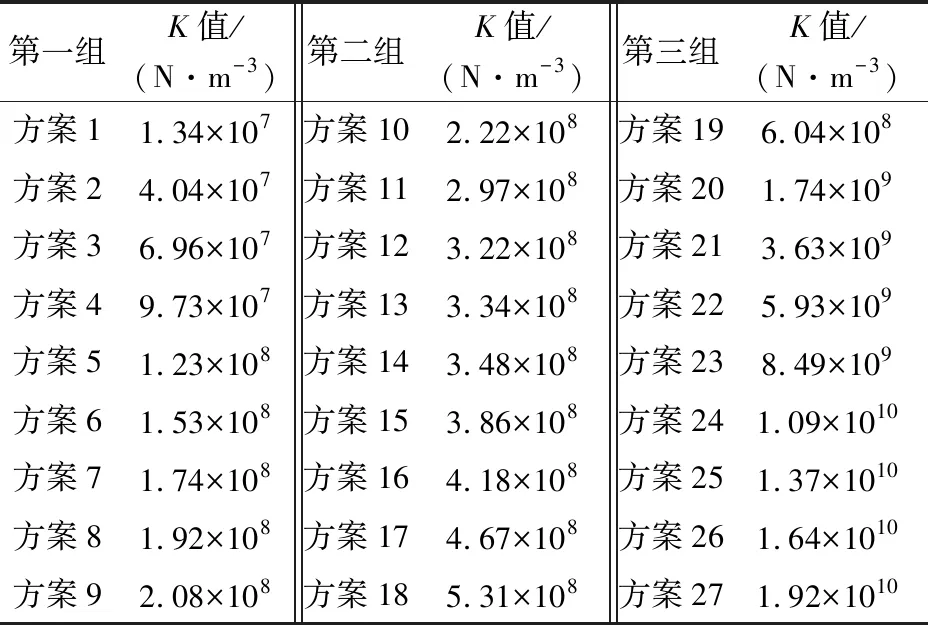
表2 各组方案嵌固段岩体地基水平抗力系数K值的取值
由表1和表2可知,嵌固段岩体地基水平抗力系数K值与岩体的弹性模量成正比,即随着岩体弹性模量E的增加K值逐渐增大;而嵌固段岩体地基水平抗力系数K值与岩体的泊松比成反比,即随着岩体泊松比υ的增加K值逐渐减小。因此,假定它们三者之间关系式为
则由Origin软件通过多元统计分析,分别拟合嵌固段岩体地基水平抗力系数K值与三组方案岩体变形参数的关系,其函数关系式如下:
(1×108≤E<1×109),R2=0.987 95;
(1×109≤E<1×1010),R2=0.927 06;
(1×1010≤E<1×1011),R2=0.995 67
式中:E为岩体的弹性模量(MPa);υ为岩体的泊松比。
由上述函数关系式可知,其能够很好地反映嵌固段岩体地基水平抗力系数与岩体弹性模量和泊松比的关系,且决定系数(R2)都较高,表明具有很好的拟合度。
3 实例应用与分析
本文以秭归县谭家湾滑坡抗滑桩优化设计为工程实例,将《秭归县谭家湾滑坡治理工程施工图设计》中所取的嵌固段岩体地基水平抗力系数K值与本文根据嵌固段岩体地基水平抗力系数与嵌固段岩体变形参数的函数关系式计算得到的嵌固段岩体地基水平抗力系数K值进行了对比分析,以验证本研究嵌固段岩体地基水平抗力系数K值取值的可靠性。
3.1 滑坡治理工程概况
谭家湾滑坡地处湖北省秭归县西北部水田坝乡上坝村二组,袁水河右岸,与集镇相距约2 km,地理坐标为东经110°40′~110°41′、北纬31°05′~30°06′,其西邻泄滩乡,东北至兴山县,南接归州镇。该滑坡的地质条件如下。
(1) 滑坡结构特征:谭家湾滑坡位于袁水河右岸斜坡地带,斜坡倾北东,地貌上微凹。区内出露的基岩为侏罗系上统蓬莱镇组(J3p)长石石英砂岩,基岩上部第四系(Q)覆盖层主要有滑坡堆积(Qdel)、洪积(Qpl)、残坡积(Qedl)和崩坡积(Qcol+dl)物质,主要成分为碎块石土夹黏性土,厚度不等。滑坡在平面上呈不规则长方形,纵向长为350~370 m;滑坡前缘、中部及后缘宽度差异不大,在215~240 m之间;滑坡后缘高程为311~320 m,前缘与袁水河漫滩相接,高程在164~167 m之间。
(2) 地质构造:研究区域处在扬子准地台上扬子台褶带台缘秭归盆地南部,位于牛口断裂和水田坝断裂之间相对稳定的地块上。勘察区处在老鹰沟向斜西翼,岩层产状为NE∠20~25°,岩体裂隙按展布方向分为3组:第一组,倾向为70°∠73°,裂面平直;第二组,倾向为345~350°∠60~80°;第三组,倾向为130~140°∠65°。新构造运动以来表现为对老构造格架的从属和继承,以大面积间歇性断块隆升为主,层状地貌发育。
(3) 岩石物理力学参数:对区内出露的基岩长石石英砂岩进行了单轴和三轴压缩试验,通过对获得的大量数据进行整理分析,得到长石石英砂岩的物理力学性质参数,见表3。
秭归县谭家湾滑坡治理工程剖面图,见图8。

表3 长石石英砂岩的物理力学性质参数
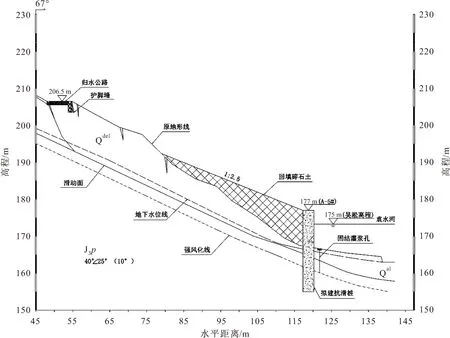
图8 秭归县谭家湾滑坡治理工程剖面图Fig.8 Section of Tanjiawan landslide project in Zigui County
3.2 抗滑桩设计计算结果的比较
在《秭归县谭家湾滑坡治理工程施工图设计》中,结合嵌固段基岩的情况以及当地滑坡治理工程的经验,在抗滑桩设计时将嵌固段岩体的地基水平抗力系数K值取为200 MN/m3,由试验确定该滑坡治理工程抗滑桩嵌固段岩体的地基水平抗力系数K值为419 MN/m3;另外。根据铁二院的《抗滑桩设计与计算》,查得长石石英砂岩的地基水平抗力系数K值为800~1 200 MN/m3,本文取为1 000 MN/m3。本文分三种情况讨论K值对抗滑桩嵌固段桩身内力和位移的影响程度,分别如下:①施工图设计中根据滑坡治理工程经验所取的K值;②依据铁二院的《抗滑桩设计与计算》中经验参数所取的K值;③依据本文所给的计算公式计算得到的K值。
通过计算可获得三种情况下抗滑桩嵌固段桩身内力和位移的对比图(见图9、图10和图11),并以情况②的计算结果为基准,分析情况①和③计算结果占情况②的百分比(见图12、图13和图14)。
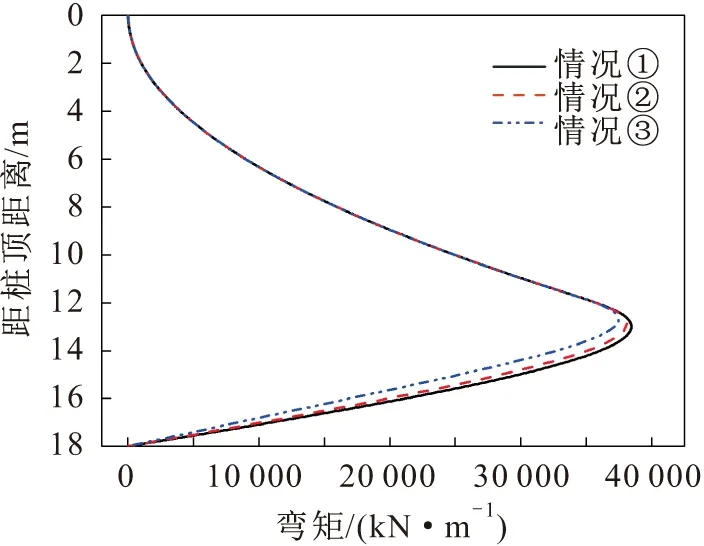
图9 抗滑桩桩身弯矩对比图Fig.9 Bending moment diagram
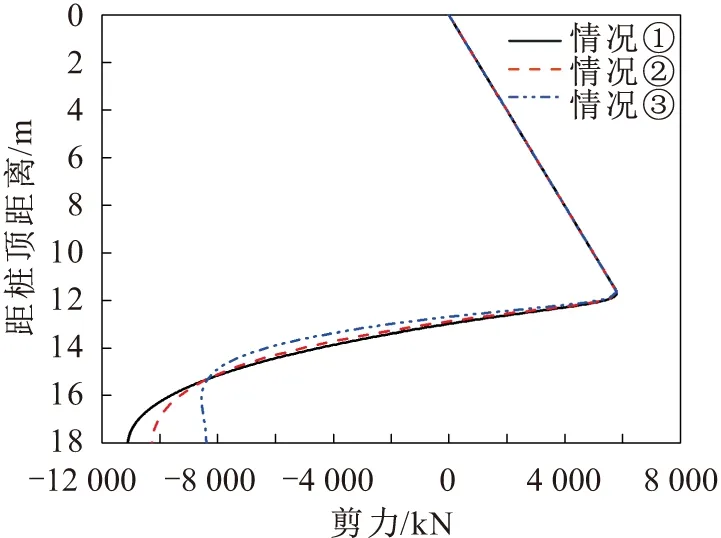
图10 抗滑桩桩身剪力对比图Fig.10 Shear diagram
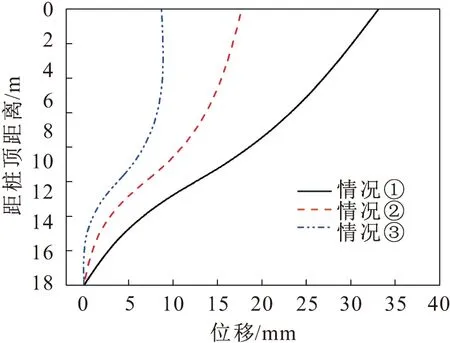
图11 抗滑桩桩身位移对比图Fig.11 Displacement diagram
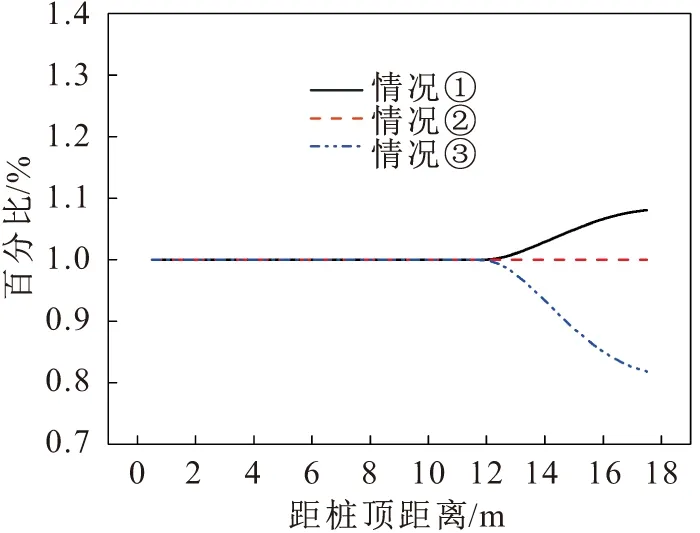
图12 抗滑桩桩身弯矩百分比对比图Fig.12 Percentage diagram of bending moment
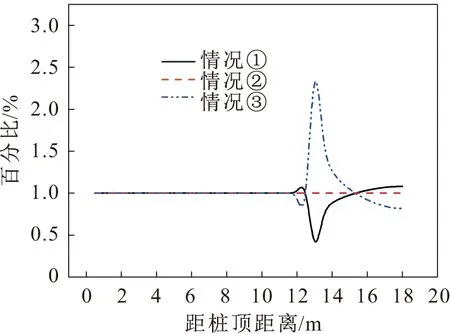
图13 抗滑桩桩身剪力百分比对比图Fig.13 Percentage diagram of shear
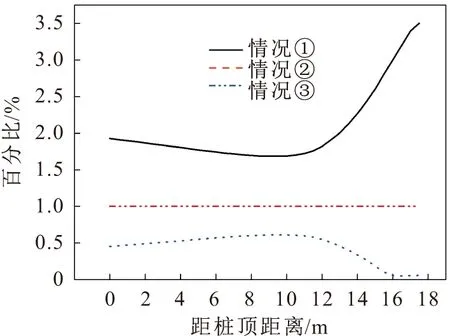
图14 抗滑桩桩身位移百分比对比图Fig.14 Percentage diagram of diaplacement
通过对比情况①、情况②和情况③的计算结果,并相较于情况②(见图9至图14),可以看出:
(1) 情况①中,弯矩和剪力在对应于情况②的受荷段部分大小相同,在对应于情况②的嵌固段部分弯矩的计算结果偏大,并且随着深度的增加弯矩的偏差量增大,弯矩最大的偏大量约8%;在对应于情况②的嵌固段部分的剪力计算结果,除在嵌固段顶部附近局部剪力偏小外,其他部分的剪力都是偏大的,在滑面附近剪力偏大量最大,约为18%;而相较于情况②的位移,整个桩身位移的计算结果偏大,且位移偏大量随着深度的增加先减小后增大,嵌固段桩身位移的偏大量普遍大于受荷段,在桩底附近位移计算结果的偏大量达到最大,约为250%。
(2) 情况③中,弯矩和剪力在对应于情况②的受荷段部分大小相同,在对应于情况②的嵌固段部分弯矩的计算结果偏小,并且随着深度的增加弯矩的偏差量增大,弯矩最大的偏小量约18%;在对应于情况②的嵌固段部分的剪力计算结果,除在嵌固段顶部附近局部剪力偏大外,其他部分的剪力都是偏小的,在滑面附近剪力偏大量最大,约为195%;而相较于情况②的位移,整个桩身位移的计算结果偏小,且位移偏小量随着深度的增加先减小后增大,嵌固段桩身位移的偏小量普遍大于受荷段,在桩底附近位移计算结果的偏小量达到最大,约为95%。
出现上述情况的原因主要是由于在抗滑桩桩身内力计算中嵌固段岩体的地基水平抗力系数K值的取值不同。相较于情况②,情况①所取的K值偏小,取值较为保守,虽然对滑坡治理工程有利,但是在配筋设计时,抗滑桩所需的抗剪箍筋最多,同时所需要的抗弯纵筋也最多,会造成材料的浪费,增加工程造价;相较于情况②,情况③所取的K值偏大,与铁二院的经验参数存在一定的误差,同时所给的K值范围过大,无法准确地确定K值。由此可见,按照本文所给出的计算公式计算得到的K值对嵌固段岩体的地基水平抗力系数K值进行优化,对抗滑桩治理工程设计具有重要的意义。
4 结 论
本文通过对嵌岩抗滑桩进行数值模拟及统计分析,基于目前“K”法中嵌固段岩体地基水平抗力系数K值的取值问题,结合工程实例进行研究,得到以下结论:
(1) 获得了具有较高拟合度的嵌固段岩体地基水平抗力系数K值与岩体弹性模量和泊松比的函数关系式,通过嵌固段岩体弹性模量和泊松比可以较准确地确定嵌固段岩体地基水平抗力系数K值。
(2) 通过数值模拟探讨了嵌固段岩体的地基水平抗力系数K值与岩体弹性模量之间的关系,结果表明:随着岩体弹性模量的增加,K值逐渐增大,嵌固段岩体的桩壁应力逐渐降低。
(3) 结合具体工程实例,对比分析了嵌固段岩体的地基水平抗力系数K值对抗滑桩桩身内力和位移的影响,并进行了抗滑桩优化设计,减少了抗滑桩钢筋用量,降低了工程造价,表明本文的方法有效地提高了嵌固段岩体地基水平抗力系数K值取值的可靠性,可为滑坡治理工程抗滑桩设计提供借鉴和参考。
