创立和剖析数学重心——思维中断点

☉浙江省温岭中学 陈 艳

突出数学的本质，加强数学内容重心的讲解是我们教师的职责所在.章建跃曾说：数学教育要着重于“三个理解”，即理解数学、理解学生、理解教育.对数学概念的理解是对数学理解的基础；对数学任务的理解是对学生理解的前提；对数学及学生的理解是对教育理解的根本.创立和剖析数学的内容重心是对这“三个理解”的最好诠释.

在数学的知识网中，那些组成数学关键的结合点，例如定理、公式及概念，我们需要重点把握.有些结合点之间会有中断，这就是我们数学学习中的思维中断点，也是我们教学中的难点，学生的易错点，所以这些中断点就是我们教学中的关键点.本文将三角函数、函数、随机变量等数学知识的中心内容结合实践来创立并剖析数学的重心——思维中断点.

一、思维中断点的创立和剖析——函数

在学习函数时，主要有这两个中断点：一个是函数有无解析式；一个是对f（x）的理解.初中是利用运动的观点，从变量的角度给出函数的概念，这样学生都只碰到类似于等这样有具体解析式的函数.但并不是所有的函数都有对应关系，也不是所有的解析式都有两个变量，这就是我们函数学习中的一个思维中断点.

（1）下表是9名同学的考试成绩，这是函数吗？

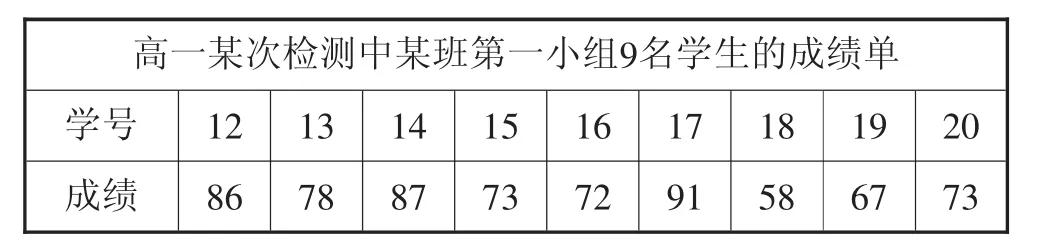
高一某次检测中某班第一小组9名学生的成绩单学号 12 13 14 15 16 17 18 19 20成绩 86 78 87 73 72 91 58 67 73

（2）图1是股票的分时图，这是函数吗？

对于这两道题而言，大部分高一的学生会觉得无从下手，因为这不符合他们初中所学的函数知识.因此，我们在教学过程中，要让学生了解到并不是每一个函数都有它的解析式，也并不是每一个函数都能用图像来表示.

图1

学习函数时的另外一个思维中断点是对f（x）的理解，这是因为f（x）可以是任何一个函数，而且学生也很难搞清楚何为f.其实f就是function的首字母，也就是功能，是将集合A中的x转变成集合B中的f（x），也就是说f（x）是集合B与集合A中x相对应的那个数.从而让学生了解到当x确定了，f（x）也就确定了.

二、思维中断点的创立和剖析——三角函数

在初中的课程中，学生学习了锐角三角函数，而从锐角三角函数到任意角的三角函数的过程中就出现了一个中断点，这也是我们在学习任意角的三角函数时的一个思维中断点，同时也是教学中的重难点.所以，让学生对锐角三角函数有一个新的认识，是我们在讲授这一内容时的重中之重.

在学习任意角的三角函数时还存在一个思维中断点，就是将终边上的任一点放于单位圆和终边相交的位置，这样的点在学生眼中并不是任一点.所以，对于这样的问题，要引导学生从相似三角形的角度来看待这个问题，让他们理解一点：一个角的终边的变化并不会改变这个角，而确定的角的三角函数也是唯一的.课堂上，可以通过坐标、终边及化简这三个方面来讲解任意三角函数的思维中断点.我们在之前的学习中已经学过了函数，我们知道函数认知的关键点在于它的三要素，那么对于三角函数而言也是一样的，可具体的三角函数的三要素是什么还需要老师慢慢的引导.

三、思维中断点的创立和剖析——直线和平面垂直的判定

在直线和平面垂直的判定的学习过程中也有这样几个思维中断点：①直线和平面垂直的定义.②用个别直线来取代平面内的任意直线.在教学中，由于平面中的直线很难直观看到，所以学生也就很难理解“直线与平面内的所有直线垂直”，更何况平面内的直线是无穷无尽的，无法通过几条特殊直线来以偏概全.因此，课堂上可以通过图2这种“立竿见影”的题目，让学生加深理解.

这种题目通常会问这样几个问题：①图2中AB与其地面上的影子BC形成了多少度的角？②随着太阳的移动，AB在地面上的影子BC也会相应的改变，那么改变后的影子还与AB垂直吗？③AB与其地面上的影子BC始终垂直，那地面上不经过B点的直线还与AB垂直吗？

图2

为了让学生更好地理解这两个思维中断点，我们可以通过设置这样一些问题来引导他们.

（1）直线和平面垂直可以只通过直线垂直平面内的一条直线来判定吗？

（2）直线和平面垂直可以通过直线垂直平面内的两条直线来判定吗？

（3）直线和平面垂直可以通过直线垂直平面内的无数条直线来判断吗？

（4）直线和平面垂直至少要直线与平面内的几条直线垂直？

（5）直线和平面垂直要满足直线与平面内的什么直线垂直？

四、思维中断点的创立和剖析——随机变量

学生通过学习早已将随机变量印在自己的脑海以及意识中，并且在遇到一些问题时能够随机运用，只是可能学生自己心里还没有一个清晰的认知，没有意识到自己已经将随机变量运用到自己的生活中了.因此虽然学生已经在不知不觉中运用了随机变量，但是要让他们自己想出来，并将所有的试验结果都数字化还是有一定难度的.这是因为要将所有的试验结果数字化是需要学生对数学的本质有一个很好的认知，因此，学生在学习随机变量时就出现了这样的一个思维中断点，将随机变量的无意识运用转变为有意而为之这样的一个过程.在平时的教学过程中，应该不断地通过一些具体的实例来促进学生对数量化意识的塑造，以及随机变量意识的塑造.比如这样一个简单的试验：抛掷一枚一元硬币，抛掷硬币的结果只会出现一正一反这两种结果，可是这一正一反的结果并不具备数量的本质，那要让学生怎么顺其自然地想要通过一些方法进行下一步的研究并且用很简便的数字来体现一正一反的结果呢？在教学中，不断抛出以下这样的问题来让学生自己思考何为随机变量，以及它的定义是什么.

第一个问题：如果我们抛掷一枚骰子，那么可能会出现哪些结果，而又有哪些数字可以用来表示这些结果呢？

第二个问题：如果我们选择一个英文字母来体现这些数字，就像我们选择x来代表这些数字，那么x可以取哪些数值呢？

第三个问题：英文字母x具备哪些特点，而这些特点我们又可以怎样理解呢？

以上的三个问题都可以构造随机变量概念上的形式.当然，要对随机变量进行更加深刻的理解，仅仅依靠这样几个问题是远远不够的，我们还应当结合函数的知识点，同时还要探究离散型随机变量的分布列等.

要结合函数的知识点来加深对随机变量的理解，这又给学生在学习随机变量上带来了另一个思维中断点.这是因为，函数代表的是变量之间确定的关系，但随机变量代表的是变量之间并没有确定的关系，随机变量只是用来表示随机现象所展现的规律，并不是想通过随机变量来预料可能会出现的结果.有一点特别重要，我们通过随机变量了解到结果的可能性或者说是结果的规定，但这并不意味着我们就能改变结果的随机性.想通过一节课的时间就让学生理解到概率统计中的不确定性是不可能的，这只能在漫长的学习生活中慢慢渗透.

我们在学习中的思维中断点不可能只存在于这几个地方，还有可能存在于一些衔接的知识点上.在教学中，我们应该多多关注知识的思维中断点，更好地衔接前后知识，加强学生对数学的兴趣，让他们更有动力地去学好数学.讲解这些思维中断点是为了更好地理解数学、理解学生、理解教学，而思维中断点的讲解离不开综合把握.这也就要求我们要在教育中，更多地关注学生的综合发展，选择与他们认知规律一致的教学内容和活动，让他们的身心与学问共同发展.对老师而言，在教学中多多关注思维中断点也能够使其在教学中更加自然流畅；对学生而言，老师多多讲解他们的思维中断点，也能加强他们理解的效率，使课堂与教材衔接得更加自然.