大道至简 悟在天成——数学教学的坚守与创新

☉江苏省南通中学 季 铮

随着高中数学新课标的实施，新一轮的教育教学改革又如火如荼地在各地展开.“学导式”、“翻转课堂”等课堂教学模式大行其道，高中数学的课堂教学颇有百花齐放的味道.每每遇到一些公开课、比赛课，任课教师无不使尽浑身解数，力求课堂教学方式的创新以吸引眼球.而笔者认为，数学课堂教学的目标：学生数学核心素养的提升，无非就是让学生亲身经历知识的发生、发展过程，在上述过程中提升发现问题、分析问题和解决问题的能力而已.

然而就这样一个看似简单的目标，很多时候却无法在课堂教学中得以实现.就比如等差、等比数列的求和，甚至在一些小学课堂上，老师就已经开始教授学生“倒序相加法”和“错位相减法”，然而这些方法的习得，只是老师简单的讲授与告知，丝毫没有学生自主的思考与感悟，学习这些方法、技巧的目的就是为多解几道题而已.在这样的教学模式下，一些学生的确会在一些考试甚至竞赛中表现出超出同龄学生的优势，然而这样的教育会培养出类似高斯的大数学家吗？然而恰恰是这样的教学方式扼杀了多少小高斯.

因此，数学课堂教学的实质就是再现数学家发现问题、提出问题、分析问题、解决问题的情景，让学生亲身经历上述过程，在过程中掌握知识、发展能力、提升素养.教学方式方法的选择、现代教育技术手段的运用都应服从于这一目标.接下来，笔者就结合几个教学案例来说明笔者的一些实践与思考.

案例一：函数的单调性

苏教版函数的简单性质一节，函数的单调性是由气温变化图引出的，通过指出气温在哪些时段逐渐升高或下降，旨在通过生活实例感受单调性的意义，并在此基础上提出问题：如何用数学语言刻画上述时段内，随着时间的增加气温逐渐升高的这一特征？上述情境的设置很好地体现了数学源于对现实世界的抽象，可是数学的味道似乎少了一些.

在上节课学习了函数的表示方法的基础上，笔者在本节课首先要求学生画出函数f（x）=|x2-4|的图像（如图1），在此基础上，请学生结合图像指出y随着x的变化而发生了怎样的变化，从而引导学生从图像的变化趋势出发，用自然语言定性地描述y随着x的变化而变化的过程.在图形语言及文字语言描述上述变化过程的基础上提出问题.

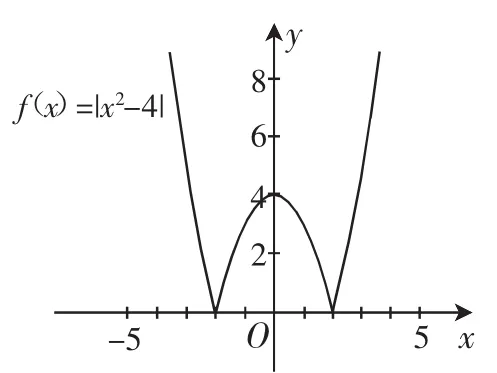
图1

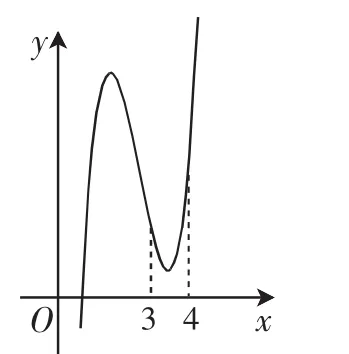
图2

师：如何从数的角度验证函数f（x）=|x2-4|在区间（2，+∞）上y随着x的增大而增大？

生1：可以在（2，+∞）的区间内取两个数，例如f（3），f（4），通过比较两者的大小来说明.

分析：学生的这个想法源于特殊化的认识，如果明确了函数在该区间上是恒单调的，这个方法对于判断函数在该区间上是单调递增亦或是单调递减是有效的，而且还非常方便.但是，如果函数在该区间上不是恒单调的，则会存在问题.作为老师，不应急于评价，应把该生的想法抛给其他同学进行讨论辨析.事实上，学生在讨论以后，给出了意见并画出了反例.

生2：图2是就是一个反例，所以仅由f（3）＜f（4），不一定能说明在（2，+∞）上y随着x的增大而增大.

分析：学生有针对性地画出反例来驳斥上述错误观点是本节课的亮点，说明学生对函数单调性的理解形成了一定的认识.

师：既然两个点不能说明，那么三个点、四个点可以吗？

生3：必须验证该区间上的无数个点，这就有些麻烦.

生4：无数个点也不可以，因为在刚才所画的函数图像上，虽然也有无数个点满足当x1＜x2＜…＜xn时，f（x1）＜f（x2）＜…＜f（xn），但是仍然不能得到在（2，+∞）上y随着x的增大而增大.

师：那么必须满足什么条件才能说明f（x）在（2，+∞）上y随着x的增大而增大.

生5：必须要f（x）图像上的所有点都满足当x1＜x2＜…＜xn时，f（x1）＜f（x2）＜…＜f（xn），才能说明f（x）在（2，+∞）上y随着x的增大而增大.

分析：学生的思考又上升了一个台阶，从函数图像上取两个特殊点到从函数图像上取无数个点，看似实现了从有限到无限的转变，但没有触及函数单调性定义的本质.这时，学生结合前面所画的反例在此基础上提出验证图像上的所有点，这就说明学生已经深刻理解了“无数”与“所有”的区别.

师：那怎么说明f（x）图像上的所有点都满足上述要求呢？

生6：所有点都满足即区间（2，+∞）内的任意两点都满足，因此可以在（2，+∞）内任取两点x1，x2，说明当x1＜x2时，均有f（x1）＜f（x2）.

分析：定义的探求最后还是回到了两个点的比较上，但从两个特殊点到任意两点的螺旋上升的探求过程是学生深刻理解定义的不可多得的重要经历和体验.

至此，函数单调性的定义就呼之欲出了，回顾学生的探究过程，经历了从特殊到一般的过程，同时举反例、交流讨论等学习方式也加深了学生对概念本质的理解，以及“所有”与“无数”的区别.

案例二：圆锥曲线的统一定义

苏教版圆锥曲线的统一定义一节，教材则指出“平面内到一个定点F的距离和到一条定直线l（F不在l上）的距离的比等于1的动点P的轨迹是抛物线”，然后提出问题“当这个比值是一个不等于1的常数时，动点P的轨迹又是什么曲线呢？”对比上一节抛物线的定义：“抛物线是平面内到一个定点F和一条定直线l（F不在l上）距离相等的点的轨迹，点F叫做焦点，l叫做准线”.教材则直接将“距离相等”改为“距离的比等于1”，从而得到圆锥曲线统一定义的雏形.这种处理弱化了学生探究圆锥曲线共性特征的思维过程.

教学过程中，笔者首先请同学们回顾了三种圆锥曲线都是由平面截圆锥面形成的，因此，这三种圆锥曲线应该具有一定的共性，从而为本节课的学习提供了依据.接下来，再请学生回顾这三种圆锥曲线的定义，对比定义，明确两种研究方向，方案一：将椭圆和双曲线的定义朝着抛物线定义的方向转化；方案二：将抛物线的定义朝着椭圆和双曲线的定义方向转化.学生注意到抛物线只有一个焦点，无法将定义写成类似椭圆或双曲线的形式，从而明确了转化的方向.

师：抛物线是平面内到一个定点F和一条定直线l（F不在l上）距离相等的点的轨迹.那么椭圆、双曲线可能是满足什么条件的点的轨迹呢？

生1：椭圆和双曲线是平面内到一个定点F和一条定直线l距离不相等的点的轨迹.

生2：距离不相等太笼统，PF≠d包含了PF＜d、PF＞d这两种情形，而这两种情形可能刚好对应了椭圆和双曲线两种圆锥曲线.

分析：从抛物线的定义出发，学生首先形成上述认识是非常自然的.

师：如何刻画PF＜d、PF＞d这两种不等关系？

生3：可以作差比较，即PF-d＜0、PF-d＞0，也可以作商比较，即0

生4：因为椭圆和双曲线方程刻画的是等量关系，因此应该把PF-d＜0这样的不等关系转化成等量关系，所以可以令PF-d是小于零的定值，比如：PF-d=-a（a＞0），则PF=d-a. 设P（x，y）、F（c，0），直线l：x=m，则|x-m|-a，两边平方得y2=（2c-2m）x-2a|x-m|+a2+m2-c2，从方程的结构看该曲线如果存在，一定不是椭圆或双曲线.

分析：通过作差和作商的方式来刻画这两种不等关系源于学生已有的学习经验，但考虑到曲线方程刻画的是等量关系，所以有必要将上述不等关系转化成等量关系，但具体是用作差还是作商来刻画，对于学生而言没有明确的指向，通过实验探究、合情推理的方式来进行探索，这样的过程妙不可言.

通过对上述案例的分析，笔者认为课堂教学方式应该随着教育技术、教育理念的发展进行创新，充分发挥互联网的功能，提供给学生多渠道获取知识的途径，帮助学生多角度的认知、建构知识体系.但是，课堂教学不应只为了创新而创新，华而不实的课堂无益于学生的发展及思维品质的提升，反而会对学生知识、方法的习得产生一定的干扰.应给予学生充分思考、探究的空间与时间，让学生亲身经历知识的发生、发展过程，并在此过程中形成分析问题、解决问题的能力，才是我们的课堂教学应该坚守的底线.