变厚齿轮连续展成磨削数值模拟研究

操 兵，庞 源，付 扬

（重庆大学机械传动国家重点实验室，重庆400044）

0 引言

变厚齿轮是一种更普通的渐开线齿轮。其主要几何特点是：沿齿轮轴线方向，变位系数及齿厚呈线性变化。变厚齿轮副可以实现平行轴、相交轴以及交错轴传动；通过调整齿轮副相对轴向位置实现无侧隙的精密传动。变厚齿轮传动还具有传动精度高、噪声小、可实现小倾角传动等优点。因此，被广泛应用在精密传动机构、无侧隙机器人RV减速器、船舶齿轮箱以及汽车传动系统等方面。

目前，国内外学者对变厚齿轮的加工进行大量研究。日本学者Mitome[1-2]根据变厚齿轮的几何特性，提出了往复式磨削、基座倾斜式滚齿法以及基座滑移式滚齿法，通过实际加工实验证明，基座倾斜式滚齿法是最实用的方法。毛建忠等人[3-4]提出了使用插齿机加工变厚齿轮的方法，探讨了刀具的插齿角度对变厚齿轮齿厚的影响，并提出得到了最优的插齿角度优化方法。温建民等[5]提出了使用大平面砂轮磨齿机加工非渐开线变厚齿轮的方法，通过实验验证了所提方法的可行性。2018年，李国龙等[6]根据变厚齿轮的成形特点，提出了使用锥形蜗杆砂轮连续展成磨削变厚齿轮的方面，通过加工仿真实验验证了所提磨削方法的正确性，实现了变厚齿轮的高效、精密磨削。

随着传动系统对传动精度以及传动噪声等要求的提高，变厚齿轮的高精、高效制造以及复杂修形变厚齿轮的制造是变厚齿轮的加工趋势。加工仿真是验证加工方法和加工精度的重要手段。目前常用三维和建模软件以及一些专用软件存在设置复杂、仿真精度低等问题。本文针对变厚齿轮的连续展成磨削方法，建立了锥形蜗杆的数学模型和锥形蜗杆磨削变厚齿轮的数学模型。

1 锥形蜗杆参数设计

图1是锥形蜗杆加工变厚齿轮的示意图。为简单起见，用锥台示意锥形蜗杆。图中：平面Q为过锥形蜗杆轴线的平面；平面P为产型齿条的中性面；直线L为平面P、Q的交线；γ是锥形蜗杆的锥角；βI是锥形蜗杆的安装角。根据文献1，为实现无干涉的连续展成磨削变厚齿轮，以上几何元素需满足以下条件：①锥形蜗杆轴线与面YOZ平行；②平面P与平面Q垂直。

图1 锥形蜗杆加工变厚齿轮示意图

为方便计算，建立了如图2所示的坐标系。图中：δ是变厚齿轮的轴向后角，P1是平面Q与产型齿条中性面交线与轴Z的交点，P2是平面Q与面YOZ的交线和轴Y的交点，P3是平面Q与产型齿条中性面交线与面XOY的交点。令点的X、Y、Z轴的坐标分量为 x1、y1、z1，根据前述的几何条件，可得点 P3的坐标分量 x3、y3、z3。

图2 锥形蜗杆参数计算坐标系

式中：β为变厚齿轮螺旋角；λ为锥形蜗杆的平均导程角。

因为平面Q与平面P垂直，可得点P2的坐标分量

由此计算锥形蜗杆的锥角γ及安装角βI：

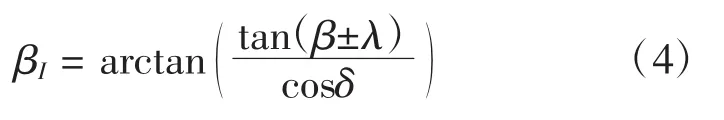
锥形蜗杆的左右齿形角 αl、αr：

式中：αn为产型齿条的法向压力角。

2 锥形蜗杆磨削变厚齿轮模型

2.1 锥形蜗杆模型

锥形蜗杆的左右齿面可以看成是由蜗杆左右轴截面廓形沿锥形螺旋线扫略生成。图3是锥形蜗杆齿面示意图。图中：坐标系Sc为参考坐标系，坐标系Sm为可动坐标系；锥形蜗杆左右齿面轴截面廓线与坐标系Sm固连；在锥形蜗杆的大端，坐标系Sc与Sm原点的距离为RB（锥形蜗杆大端分度圆半径）。

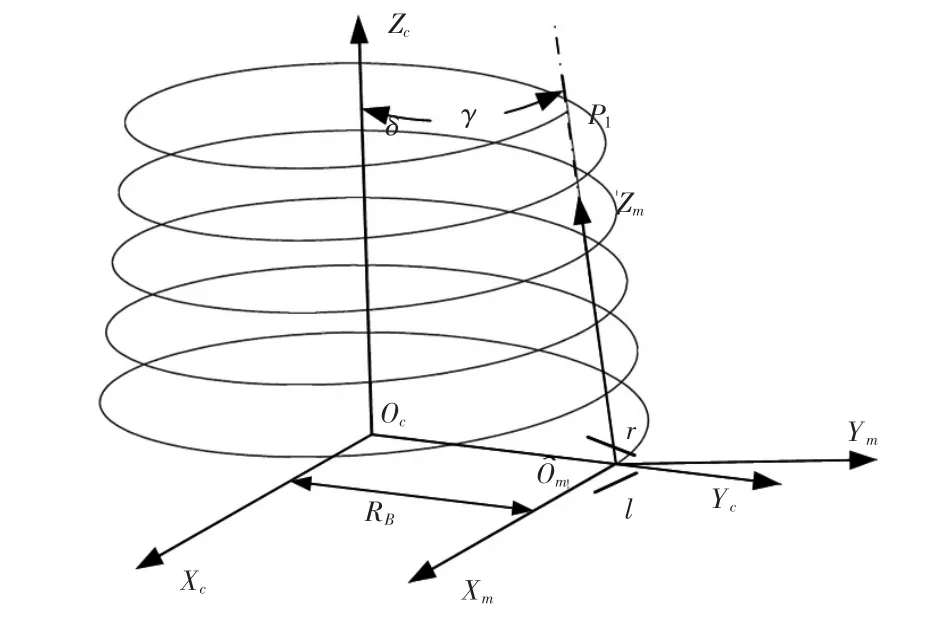
图3 锥形蜗杆示意图

在坐标系Sm中，锥形蜗杆左右齿面轴截面廓线的方程如下：

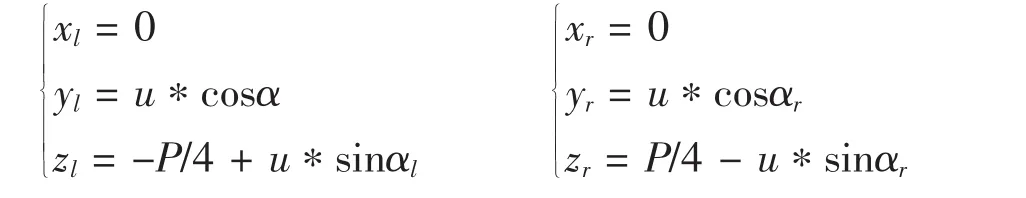
式中：u为自由变量；P为锥形蜗杆的平均导程。坐标系Sc与坐标系Sm间的转换矩阵Mcm为：

综上，可得到锥形蜗杆左右齿面的方程：

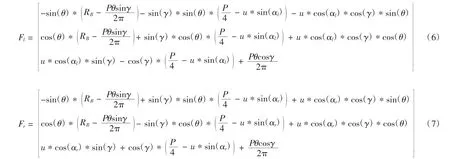
2.2 锥形蜗杆磨削变厚齿轮建模

与普通圆柱渐开线齿轮连续展成磨削一样，锥形蜗杆磨削变厚齿轮过程中，锥形蜗杆与变厚齿轮的齿面是点接触。每一瞬时的接触点就是锥形蜗杆与变厚齿轮的啮合点，通过计算锥形蜗杆每一时刻与齿面的啮合点，可以算出完整的变厚齿轮的齿面。

图4是锥形蜗杆磨削变厚齿轮的坐标系示意图。图中：坐标系Sf与坐标系S1为固定坐标系，其中轴Zf与变厚齿轮的轴线共线，轴Z1与锥形蜗杆的轴线平行，当锥形蜗杆在初始位置时锥形蜗杆的轴线与轴Z1重合；坐标系Sg与变厚齿轮固连，随变厚齿轮绕轴线做旋转运动；坐标系Sc与锥形蜗杆固连，随锥形蜗杆做自身轴线的转动和平动；θg是齿轮绕自身轴线旋转角度；θc是锥形蜗杆绕自身轴线旋转的角度。各坐标系间的转换矩阵如下：

图4 锥形蜗杆磨削变厚齿轮的坐标系示意图

在锥形蜗杆磨削变厚齿轮过程中，锥形蜗杆主要完成绕自身轴线的运动与沿齿轮轴线直线运动，这两个运动是相互独立；变厚齿轮仅做绕自身轴线的转动。所以，锥形蜗杆磨削变厚齿轮是一个双自由度的啮合运动。根据文献[7]，锥形蜗杆与变厚齿轮的啮合点满足啮合方程：

啮合方程在任意坐标系中均是成立的。为计算方便，将锥形蜗杆磨削变厚齿轮啮合方程的求解统一到坐标系S1中。在坐标系S1中锥形蜗杆左右齿面的方程为：

在坐标系S1中，锥形蜗杆左右齿面上任一点处的法向量为：

令锥形蜗杆绕自身轴线的旋转角速度为ωc，沿齿轮轴线斜向下的移动速度为Vc。对于锥形蜗杆左右齿面上任意一点，在坐标系S1中的速度可以表示为：

齿轮的转动角速度ωg不仅受锥形蜗杆的转动速度ωc的影响，还受锥形蜗杆的移动速度Vc的影响。ωg的计算公式如下：

式中：zc、zg分别是锥形蜗杆的头数和变厚齿轮齿数；r为变厚齿轮分度圆半径。

在坐标系S1中，变厚齿轮齿面上任意点处速度为：

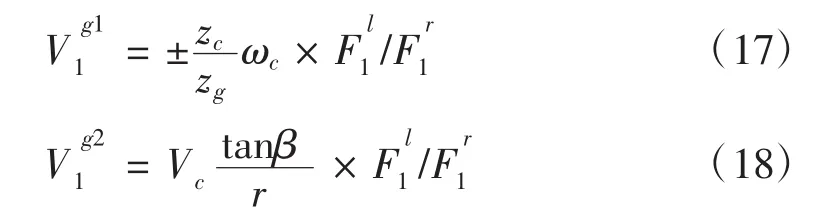
所以，变厚齿轮左右齿面与变厚齿轮齿面任意点处的相对速度为：

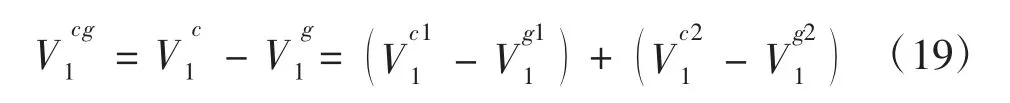
由此，可以得到锥形蜗杆磨削变厚齿轮的啮合方程：

其是一个含有3个未知量u、θ、θc非线性方程。

由于 ωc、Vc独立，上式可以分成 f1、f2两个独立方程：

在求解时，通过给定从锥形蜗杆齿根（齿顶）变化的u的值，通过上式可求解θ、θc。假设啮合点在锥形蜗杆齿根处（u=u0）的 θ、θc值分别是 θ0、θc0；锥形蜗杆齿面任一点为啮合点时的 u、θ、θc为 ui、θi、θci。将啮合点的坐标转换到齿轮坐标系Sg中即可得到变厚齿轮齿面。可得到变厚齿轮左齿面表达式：

转换矩阵Mgf中齿轮转动角度θg的计算如下：

3 数字实例

针对表1的变厚齿轮数据，设计了锥形蜗杆参数（表2），并利用所建立的锥形蜗杆磨削变厚齿轮齿轮的数字模型计算变厚齿轮仿真模型。并将仿真模型与理论变厚齿轮进行了对比。

表1 变厚齿轮基本参数

表2 锥形蜗杆参数

图5是锥形蜗杆磨削变厚齿轮数字仿真得到的变厚齿轮左右齿面。将由数字模型算得的齿面与理论变厚齿轮的齿廓对比，得到数字模型与理论齿廓间的全齿面误差（如图5所示）。

图5 变厚齿轮仿真齿面

由图6可知，有数字仿真算得的变厚齿轮磨削齿面与理论的齿面间误差极小，最大误差仅0.15 μm。并且，误差具有在齿廓方向呈抛物线状的特点。

图6 数字仿真模型与理论廓形全齿面误差

4 结论

本文针对锥形蜗杆磨削变厚齿轮的数字仿真进行了研究。对展成磨削变厚齿轮的锥形蜗杆的设计方法进行了推导，建立了锥形蜗杆的数学模型。分析了变厚齿轮连续展成磨削的运动过程，建立锥形蜗杆磨削的变厚齿轮的数学模型。最后，以某一变厚齿轮为例，将由锥形蜗杆磨削变厚齿轮仿真模型得到的数字齿面与理论变厚齿轮的齿面进行了全齿面的误差分析，结果显示误差极小，验证了建立模型的正确。