变式教学在初中数学教学中的作用

汪斌

变式教学是数学教学的优良传统，而一题多变是应用教学中常用的一种教学手段，它正是在掌握例题典型性的基础上，充分发挥例题的可变性，通过条件的变化或者是问题、图形的变化，使知识延伸.如果在教学中我们能灵活运用，将能起到以下作用.

一、有利于学生掌握基础的定理法则

教师充分利用特例、实验等手段，设计一系列问题变式，利用问题变式来明确定理、公式和法则的条件、结论、适用范围等关键之处，进而培养学生逻辑推理论证能力和正确的演算能力.引发学生联想，培养学生数学思维的灵活性和思考问题的深刻性.当然教师将问题转化成一名学生比较熟悉的变式从而得到另一个相关的问题，再从相关的问题的解答过程或结论中，通过归纳或者类比等方法迁移得到原问题的结论或者某种解题的启示.这样的变式，有利于学生掌握知识的本质.

例如，“求证顺次连接四边形各边中点所得的四边形是平行四边形.”学生解决这个问题很容易的，教师还可以顺题深入提出以下问题.

变式1：顺次连接平行四边形各边中点所得的四边形是什么图形？

变式2：顺次连接矩形各边中点所得的四边形是什么图形？

变式3：顺次连接菱形各邊中点所得的四边形是什么图形？

变式4：顺次连接正方形各边中点所得的四边形是什么图形？

变式5：顺次连接什么四边形各边中点可以得到平行四边形？

变式6：顺次连接什么四边形各边中点可以得到矩形？

变式7：顺次连接什么四边形各边中点可以得到菱形？

变式8：顺次连接什么四边形各边中点可以得到正方形

学生通过画出图像，证明可知：中点四边形的边与原四边形的对角线有密切关系，这是一个动态图形的系列问题：无论原来的四边形的形状怎样改变，顺次连接它各边的中点所得的四边形最起码是平行四边形.而且平行四边形又包含了矩形、菱形、正方形，这时，原四边形又怎样的变化呢？使学生对中点四边形与原四边形的形状的变化规律有一个系统的认识.

由特殊的四边形对角线的特征和特殊的四边形的判定方法，变式的问题就能迎刃而解.通过这样一系列变式，使学生充分掌握了四边形、平行四边形与特殊的平行四边形的性质，以及四边形、平行四边形与特殊的平行四边形对角线的区别，为进行数学问题演变奠定了坚实的知识基础.

变式教学应该能够体现数学的层递性.对题目进行了大胆的拓广，由易到难.不仅锻炼了学生用类比的方法去思考和学习，而且促进学生对解决问题的思路理解得更为透彻.

二、举一反三、由浅入深有利于问题的解决

数学教学离不开解题，解题的目的是通过解题深化学生对知识的理解，提升学生的思维水平，从而积累解题经验、发展能力.通过对解题方法分析与比较，揭示其中的思想方法以及各自的特点、适用范围等，拓展学生的解题思路.

例如，求一元二次方程：x2-2x-8=0的根.学生在解一元二次方程方法很多，有配方法、公式法、因式分解法.学习了二次函数，教师将一元二次方程与二次函数联系起来，可以进行以下变式：

变式1：你能结合二次函数图像求出x2-2x-8>0的x取值范围吗？

变式2：你能结合二次函数图像求出x2-2x-8<0的x取值范围吗？

学生不解不等式而是通过二次函数图像就能将不等式的解求出来.这样通过变式让学生更好地理解二次函数与不等式的联系，学会用二次函数的图像来解题，培养了学生数形结合的思想，开阔了学生的思维，加深了对二次函数图像的理解.

数学中的一题多变应能够体现知识的一定规律和一定的关联，便于学生思考问题时思路的发展.利用一系列的变式培养学生的观察能力，了解数学从简单到复杂，从一般到特殊的探索规律.用不同的思路去分析，不仅使得学生对思考的问题由浅入深，而且锻炼了学生类比推理能力和归纳能力.

三、有利于形成良好的认知结构

通过变式设计的例题，前面的例题的部分题目信息可以直接转移到后面的例题中.因而，可以解决审题时间，提高课堂效率，通过变式设计的例题，可以知道相互之间在联系.正因为这种内在的联系，巧妙地运用变式设计例题，不仅可以提高课堂效率，还有利于学生形成良好的认知结构.

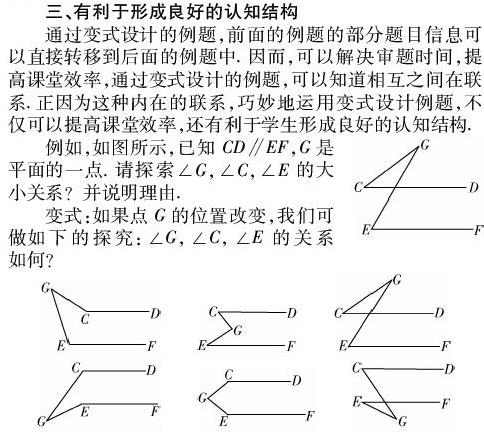
例如，如图所示，已知CD∥EF，G是平面的一点.请探索∠G，∠C，∠E的大小关系？并说明理由.

变式：如果点G的位置改变，我们可做如下的探究：∠G，∠C，∠E的关系如何？

通过题目的变式，帮助学生加深理解平行线的性质、三角形外角的性质，随着点G的不同变化，结论也会不同，但解法却如出一辙，都是过折点G作平行线构造“三线八角”，也可用三角形的外角性质来解决问题.

以上几种变式题虽然条件发生变化，但解题的思路是不变的.教师可以在讲解其中的某一题时，举一反三，同时讲解其他几种情形，甚至还可以“一题多变”.一题多变，以点串线，联想开拓，对培养学生的发散思维十分有利.教师可以借用某道典型例题，适当变换、拓展，充分拓展原题的解题思路和方法，从而探索问题的本质，达到真正的教学目的.这样在变式练习中培养了学生思维的变通性.

通过恰当的变式教学能起到调动学生主动性、激发学习兴趣.利用学生渴求新知的心理，这样会吸引学生，激发学生强烈的兴趣和求知欲，学生自觉地去解决、去创新.变式教学可以有效地提高学生的思维.运用变式的教学方法，能提高学生的学习兴趣，有效地避免题海战术，巩固数学知识，可培养学生独立思考，举一反三的学习态度.