对问题深入思考 促学生“深度学习”

江苏省泰州市智堡实验学校

李光红 (邮编：225300)

笔者前不久翻看2018年的中考题，其中有两道题引起笔者浓厚的兴趣，进而进行了深入思考，请看这两题：

例1 (2018年无锡中考)如图1，平面直角坐标系中，已知点B的坐标为(6,4).

图1

(1)请用直尺(不带刻度)和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等.(作图不必写作法，但要保留作图痕迹.)

(2)问：(1)中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式.

分析第(1)题考虑到矩形的中心对称性，过B作BA⊥x轴于A点，过B作BC⊥y轴于C点，则△AOC≌△CBA，所以AC符合要求；第(2)题受第(1)题的启发，只要作出直线AC使△ABC与△AOC全等即可，考虑轴对称性，连接OB，作线段OB的垂直平分线分别交x轴和y轴于点A和点C，则△AOC≌△ABC，直线AC符合要求，进而求出直线AC的函数关系式.

如图1所示：

图2

进一步思考：以上共有两种作法，会不会有其他作法呢？

我们知道，若△ABC与△AOC全等，必然能使∠ABC=∠AOC=90°，△ABC与△AOC的面积相等；但是其逆命题正确吗？通过研究发现其逆命题是正确的.下面我们来证明一下：

已知：如图2所示，在平面直角坐标系中，点B的坐标为(6,4)，作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等.

求证：△ABC与△AOC全等.

证明因为∠ABC=∠AOC=90°，

所以AO2+CO2=AC2，

AB2+CB2=AC2，

所以AO2+CO2=AB2+CB2，

①

又因为△ABC与△AOC的面积相等，

所以2AO·CO=2AB·CB，

②

①+②，得：AO2+2AO·CO+CO2=AB2+2AB·CB+CB2，

即：(AO+CO)2=(AB+CB)2，

因为AO+CO>0，AB+CB>0，

所以AO+CO=AB+CB，

③

①-②，得：AO2-2AO·CO+CO2=AB2-2AB·CB+CB2，

即：(AO-CO)2=(AB-CB)2，

所以AO-CO=±(AB-CB)，

④

由③、④联立，可得：AO=AB，CO=CB或AO=CB，CO=AB.

两种情况均能得到△ABC与△AOC全等.

因此，符合条件的作法有且只有两种！

例2 (2018年南京中考)结果如此巧合！

下面是小颖对一道题目的解答.

题目如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积.

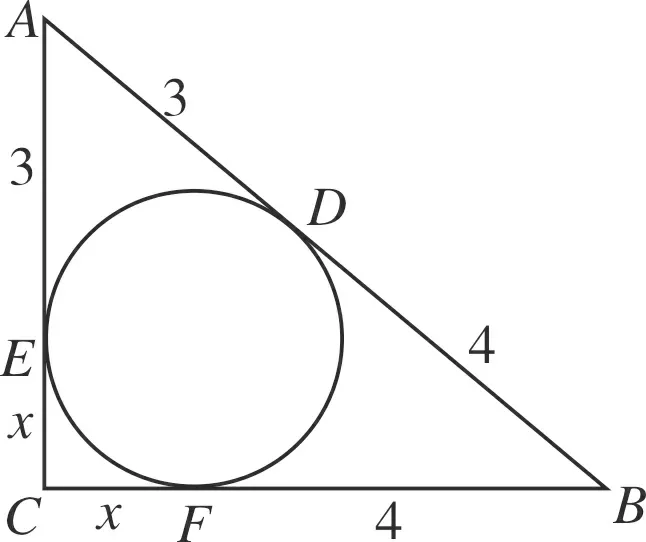
图3

解设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x.

根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x.

根据勾股定理，得(x+3)2+(x+4)2=(3+4)2.

整理，得x2+7x=12.

小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?

请你帮她完成下面的探索.

已知△ABC的内切圆与AB相切于点D，AD=m，BD=n.

可以一般化吗？

(1)若∠C=90°，求证：△ABC的面积等于mn.

倒过来思考呢？

(2)若AC·BC=2mn，求证∠C=90°.

改变一下条件……

(3)若∠C=60°，用m、n表示△ABC的面积.

分析设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x.

根据切线长定理，得AE=AD=m，BF=BD=n，CF=CE=x.第(1)(2)两小题解法省略，第(3)小题过程如下：

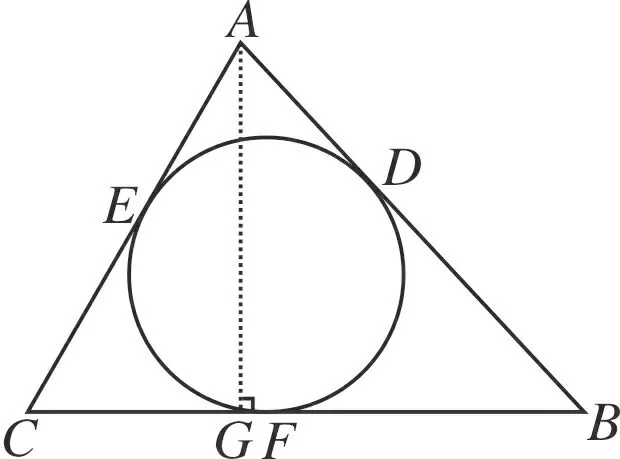
图4

(3)如图4，过点A作AG⊥BC，垂足为G.

在Rt△ABG中，根据勾股定理，得

整理，得x2+(m+n)x=3mn.

这是一道阅读理解+探索应用的题目，第(1)题把原题中AD和BD的长一般化；第(2)题是第(1)题的逆向应用；第(3)题把∠C的度数进行了变化，探索其中有无相似的规律.做完之后，感觉意犹未尽：如把∠C的度数也一般化，△ABC的面积是否也可以用含m、n及∠C的代数式表示呢？下面来研究一下：

如图4，过点A作AG⊥BC，垂足为G.

在Rt△ACG中，

AG=AC·sinC=(x+m)·sinC，

CG=AC·cosC=(x+m)·cosC.

所以BG=BC-CG=(x+n)-(x+m)·cosC.在Rt△ABG中，根据勾股定理，得

[(x+m)·sinC]2+[(x+n)-(x+m)·cosC]2=(m+n)2.

展开，得(x+m)2sin2C+(x+n)2-2(x+n)(x+m)cosC+(x+m)2cos2C=(m+n)2.

即 (x+m)2(sin2C+cos2C)+(x+n)2-2(x+n)(x+m)cosC=(m+n)2.

(x+m)2+(x+n)2-2(x+n)(x+m)cosC=(m+n)2.

x2+2mx+m2+x2+2nx+n2-2cosC·x2-2cosC·(m+n)x-2cosC·mn=m2+2mn+n2.

2(1-cosC)x2+2(1-cosC)(m+n)x=2mn(1+cosC).

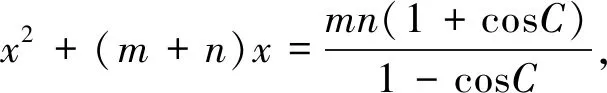
至此，发现△ABC的面积可以用含m、n及∠C的代数式表示，且第(1)、(3)题都可以通过上式得到验证.

郑毓信教授在谈到如何落实核心素养问题时，提出：我们应当努力做到“深度教学”；进而，适当的“问题引领”正是我们实现上述目标最重要的一条途径.我想，每年各地的中考题为我们提供了丰富多彩、鲜活有创意的素材，我们应该做个有心人，对这些好的素材进行深入研究.要引导学生“深度学习”，我们老师首先要对问题有“深入思考”.在“深入思考”的基础上，通过“问题引领”，即通过适当的提问，特别是启发性的问题，将学生的思维引向深入，从而使学生的思考更清晰、更深入、更全面、更合理，更有效地促进学生思维的发展.以上是本人一点浅见，供诸位同仁参考指正.