水下爆炸冲击波作用下屏蔽装药的冲击引爆理论和仿真研究

李元龙, 王金相, 申向军, 周 楠, 黄瑞源， 荣 光

(1.南京理工大学 瞬态物理国家重点实验室，南京 210094； 2.晋西集团753厂，山西 太谷 030800； 3.南京森林警察学院 刑事科学技术系，南京 210023)

目前鱼雷是水面舰艇的主要威胁之一，因此开展有效的反鱼雷技术研究关系到水面舰艇的生存。随着反鱼雷技术的日趋发展，水下爆炸冲击波逐渐成为毁伤鱼雷的最主要形式之一，而鱼雷战斗部装药则是毁伤的主要针对部分[1]。因此，研究水下爆炸冲击波对屏蔽炸药的毁伤对于硬毁伤鱼雷技术具有重要的意义。Cole[2]根据大量水下实验数据提出了经典的水下爆炸经验公式，为水下爆炸载荷的计算提供了简洁实用的方法，Zamyshlyayev[3]则在Cole的基础上，综合运用理论和试验的方法，对经验公式进行了改进。当前，对于破片撞击屏蔽炸药的冲击引爆问题，已开展了大量的研究[4-6]，从理论以及数值模拟方面建立了屏蔽炸药的临界起爆判据[7-9]，很好的描述了屏蔽炸药的起爆特性, 为冲击起爆实验和后续的可靠性研究提供了大量的参考。但这些研究大多应用于空气中屏蔽装药的起爆问题，而涉及水下爆炸冲击波的内容还较少。基于水介质中爆炸冲击波传播特性，充分考虑冲击波强度、壳体材料、厚度以及被发炸药的属性等因素开展爆炸冲击波引爆屏蔽装药条件研究是当前急需开展的研究方向，并将对反鱼雷技术提供一定的指导作用。

本文从理论上建立了水下爆炸冲击波对屏蔽装药的冲击引爆模型，利用AUTODYN仿真软件对水中冲击波的传播过程和屏蔽装药的冲击引爆进行了模拟，验证了理论计算模型的有效性，采用最小二乘法得到了临界起爆判据的参数n、K，分析了主发药质量和挡板厚度对冲击引爆PBX-9404炸药临界距离的影响。

1 水下爆炸冲击波对屏蔽装药的理论分析

1.1 水下爆炸冲击波理论

Cole通过对大量实验数据的整理，总结了水下爆炸冲击波经验公式，Zamyshlyayev在其基础上改进得到峰值压力公式为

(1)

式中：Pm为冲击波峰值压力；W为TNT炸药质量；R为测点到爆心的距离；R0为炸药初始半径。

1.2 冲击起爆判据

炸药对冲击载荷的动态响应分两种情况：一种是强冲击载荷下，炸药冲击转爆轰(SDT)；另一种是长持续脉冲时间发生的反应(LALDS)。

在强冲击波载荷作用下，炸药发生爆轰准则可表述为

p2τ=K

(2)

式中:p为炸药界面冲击波压力;τ为冲击转爆轰的时间;K为与炸药相关的参数。

在炸药界面压力p低于临界起爆压力pc情况下，长时间的低压力冲击波持续作用也会形成炸药的爆轰。在这种情况下，冲击波引发炸药爆轰准则可表述为

pnτ=K

(3)

从冲击起爆判据看，具体装药均存在一组装药临界起爆特性参数，即临界起爆压力pc、能量系数K和经验常数n。临界起爆公式广泛适用于非均质炸药的一维冲击起爆，但当在小面积上进行加载时，将出现侧向稀疏波，此时，一维短脉冲能量判据就不适用了。因此对水下冲击波作用进行合理简化，以便建立理论计算模型。假设水下爆炸冲击波为一维冲击波，壳体径向尺寸远远大于冲击波作用半径，忽略平行于冲击波传播方向的侧壁对装药的冲击作用。

1.3 冲击起爆参数计算

水下爆炸冲击波冲击起爆屏蔽装药的示意图如图1所示。水中冲击波经过一段距离的传播到达屏蔽装药挡板，在挡板与水的接触面上发生反射与透射，由于水的波阻抗小于挡板波阻抗，将在水中反射压缩波，同时，在挡板内透射一压缩波。设未经扰动的介质参数为p0、ρ0、u0=0，到达挡板界面的冲击波参数为p1、ρ1、u1、D1，屏蔽挡板厚度为h，冲击后在水和挡板中产生的冲击波速度分别为Dw和Dt，水的密度、压力和质点速度分别为ρw、pw和uw，挡板的密度、压力和质点速度分别为ρt、pt和ut。冲击波在水与挡板界面发生作用的示意图，如图2所示。

图1 冲击起爆示意图

(a) 水与挡板分界面(1)

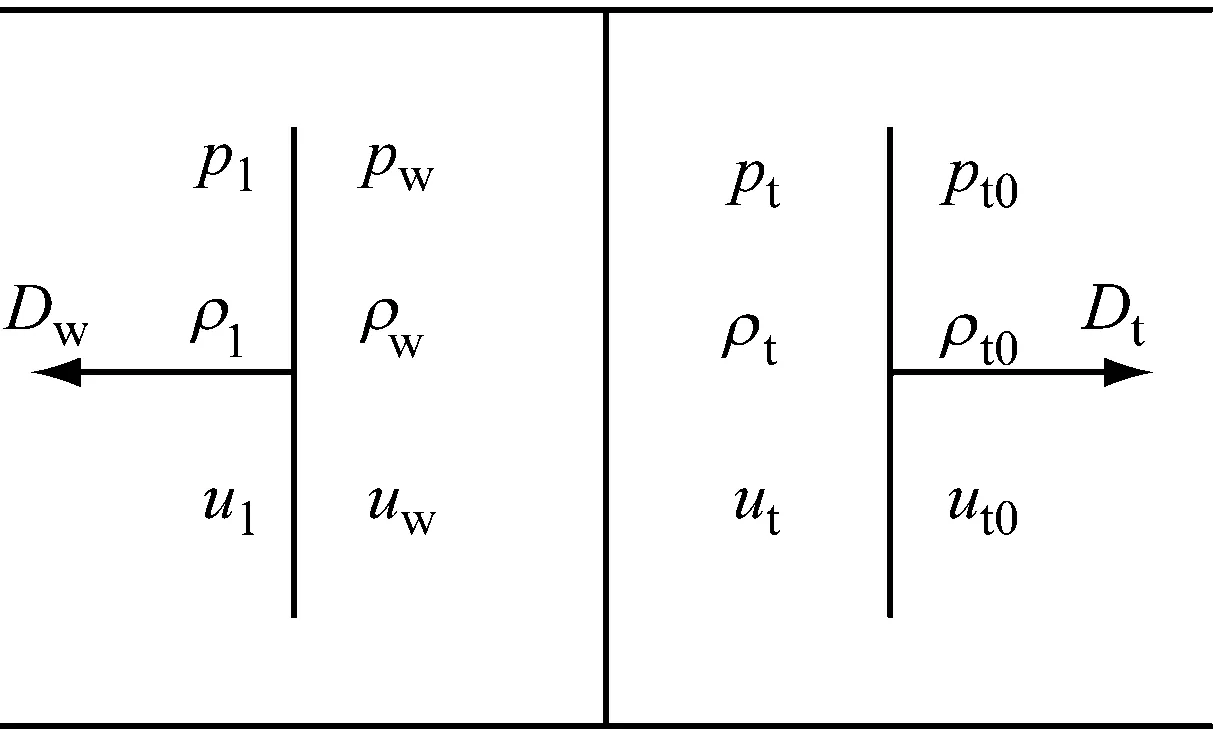
(b) 水与挡板分界面(2)

利用冲击波前后质量守恒和动量守恒，可得到水和挡板中初始冲击波压力表达式

对于水

pw=ρwDwuw

(4)

对于挡板

pt=ρtDtut

(5)

由连续边界条件可知，冲击波传播经过水和挡板的界面时，分界面上的质点运动速度和压力相等，即

2u1=uw+ut

(6)

pw=pt

(7)

利用线性Hugoniot 关系来表示材料中冲击波速度与质点速度之间的关系

Dw=aw+bwuw

(8)

Dt=at+btut

(9)

式中：aw、bw和at、bt为根据Hugoniot关系式得出的水和挡板的冲击压缩经验常数。

联立式(4)～式(9)就可以求出pw、pt、uw、ut。由于挡板材料的波阻抗的作用，冲击波在挡板中传播时将会发生衰减，其衰减规律为[10]

pt=pte-αx

(10)

式中：pi为经过挡板衰减后的冲击波压力；x为传播距离(即挡板厚度h)；α为衰减系数。参考式(4) 即可求得相应的质点速度ui。

当挡板中的冲击波传播到挡板与炸药的分界面处，由于炸药的波阻抗远小于挡板的波阻抗，在挡板和炸药的分界面处冲击波将会产生卸载反射，向挡板反射稀疏波，而向炸药透射冲击波。根据炸药与挡板界面上的动量守恒和连续条件，透射进入炸药的冲击波压力pe及质点速度ue通过下式求得

ρe(ae+beue)ue=ρt[at+bt(2ui-

ue)](2ui-ue)

(11)

pe=ρe(ae+beue)ue

(12)

式中:ae、be为炸药的Hugoniot参数，理论计算所需参数列于表1[11-12]，其中铝合金的衰减系数为α=0.029 3 mm-1[13]。

浙江省纪委督导调研组近日在暗访时发现，有些机关单位的工作微信群和政务办公群，已经成为形式主义的温床。因为“干得好不如晒得好”，所以有些基层干部，便把手机当作展示政绩的“秀场”。一天到晚，用指尖刷数字、刷进度、刷形象。据说有人为了刷下乡走访的里程，还专门到院子里或大街上溜圈。

通过式(10) ～ 式(12) 就可以求出透射到炸药中的冲击波压力。由于透射入炸药的冲击波压力远远达不到炸药的临界起爆压力，因此采用考虑长持续脉冲时间的冲击起爆准则。

表1 材料参数

2 数值模拟模型

2.1 有限元模型

利用AUTODYN软件进行数值模拟计算，由于各部分关于球形装药中心和屏蔽装药之间的垂线轴对称，故采用二维轴对称计算模型。如图3所示，主发药采用TNT球形药包，半径为15.7 cm，质量6.6 kg；挡板厚度为h，材料为铝合金；被发装药为PBX-9404炸药，主发药处于水介质中。网格采用Euler计算方法，单元尺寸为2 mm，共550 000个单元，炸药与挡板共节点。为减小爆炸过程中的边界反射效应，在水、挡板和被发药的相关位置定义流出边界条件。

图3 仿真计算模型

2.2 材料模型与状态方程

挡板的材料采用Shock状态方程，材料模型为Johnson-Cook模型，材料参数取自AUTODYN标准数据库[14]。水的状态方程采用线性多项式方程[15]，当水压缩时(μ>0)，其状态方程为

P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e

(13)

当水膨胀时(μ<0),其状态方程为

P=T1μ+T2μ2+B0ρ0e

(14)

当水既不压缩也不膨胀时(μ=0)，式(14)和式(15)可以简化为同一形式

P=B0ρ0e

(15)

式中：P为水中压力；μ为压缩比，μ=ρ/ρ0-1；e为水的内能；ρ0为水密度，取ρ0=1.00 g/cm3。A1=2.20 GPa，A2=9.54 GPa，A3=14.57 GPa，B0=0.28，B1=0.28，T1=2.20 GPa，T2=0。

主发药采用JWL状态方程，JWL状态方程定义压力为相对体积V和单位初始构形体积内能E的函数

(16)

式中：p为压力；V为相对体积；E为内能；ω、C1、C2、R1、R2为表征炸药特性的常数。取ρ0=1.63 g/cm3，C1=37.12 GPa，C2=3.231 GPa，R1=4.15，R2=0.95，ω=0.30。

PBX-9404炸药的状态方程采用Lee-Tarver点火增长模型，其相关参数见表2，此方程可较好模拟非均质炸药的冲击起爆特性[16]

G1(1-F)cFdPy+G2(1-F)eFgPz

(17)

表2 PBX-9404材料参数

式中，F为炸药燃烧质量分数，它在模拟爆轰过程中控制着炸药化学能的释放；I、b、a、x、G1、c、d、y、G2、e、g、z为参数；炸药反应物与未反应物均采用JWL状态方程。

3 分析与讨论

3.1 理论方法与数值仿真一致性分析

理论计算模型如示意图1所示。主发药TNT质量为6.6 kg,半径R0=9.9 mm，挡板厚度为h，主发药包与挡板的距离为R。理论计算结果与数值计算结果见表3。通过调整药包与挡板距离R和挡板厚度h，分析10种不同工况下对屏蔽炸药起爆的影响。将数值模拟中到达挡板压力p1、透射入炸药压力pe与理论计算结果进行对比，其中到达挡板压力仿真值与理论值最大误差为11.52%，透射入炸药压力仿真值与理论值最大误差6.75%，吻合较好，说明所建立的理论计算模型和数值仿真是一致的。

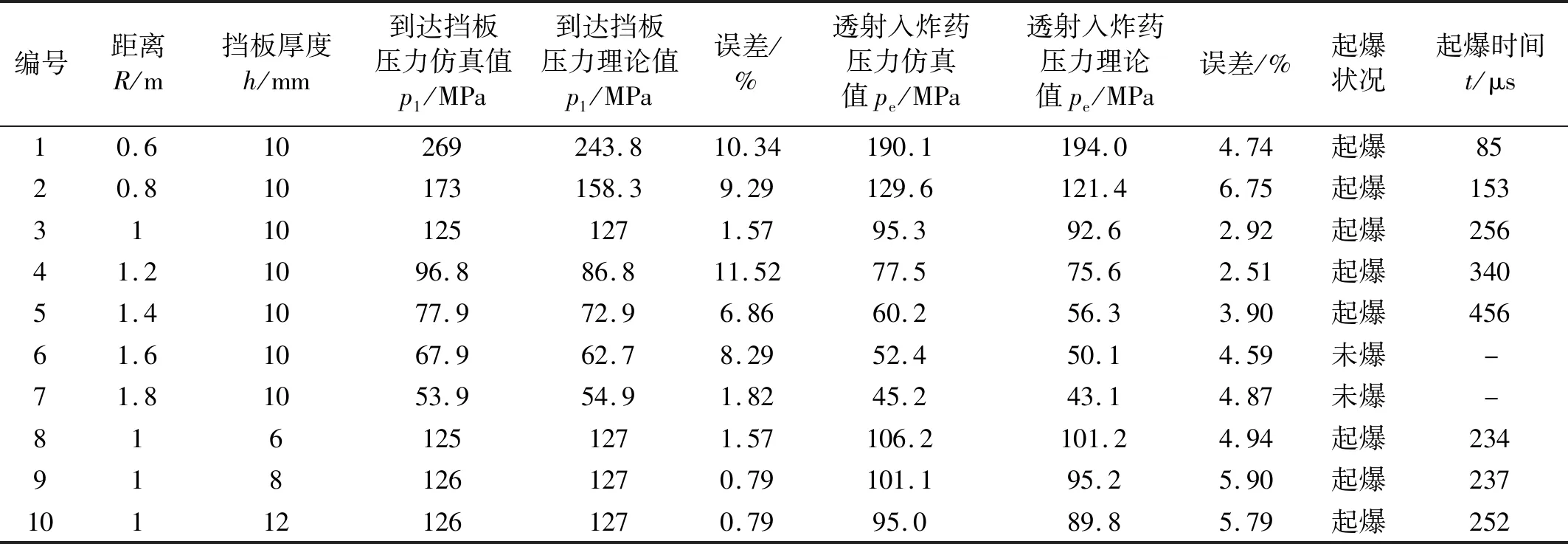
表3 数值模拟结果与理论计算结果对比表

3.2 冲击起爆过程描述

图4给出了距离主发药包1 m处，冲击引爆被发炸药的典型爆炸压力云图，模型挡板厚度为10 mm。被发炸药爆炸与否利用炸药中的压力及被发炸药的反应状态来进行判定。初始主发药被引爆，形成的爆炸冲击波在t=460 μs时到达屏蔽挡板，此时冲击波压力峰值为125 MPa，经过挡板的透射以及衰减作用传入被发炸药，冲击波在被发炸药中经过256 μs的时间后，到达被发药的临界起爆能量值并将被发炸药引爆，形成一个强压力的波阵面迅速向炸药层内传播。

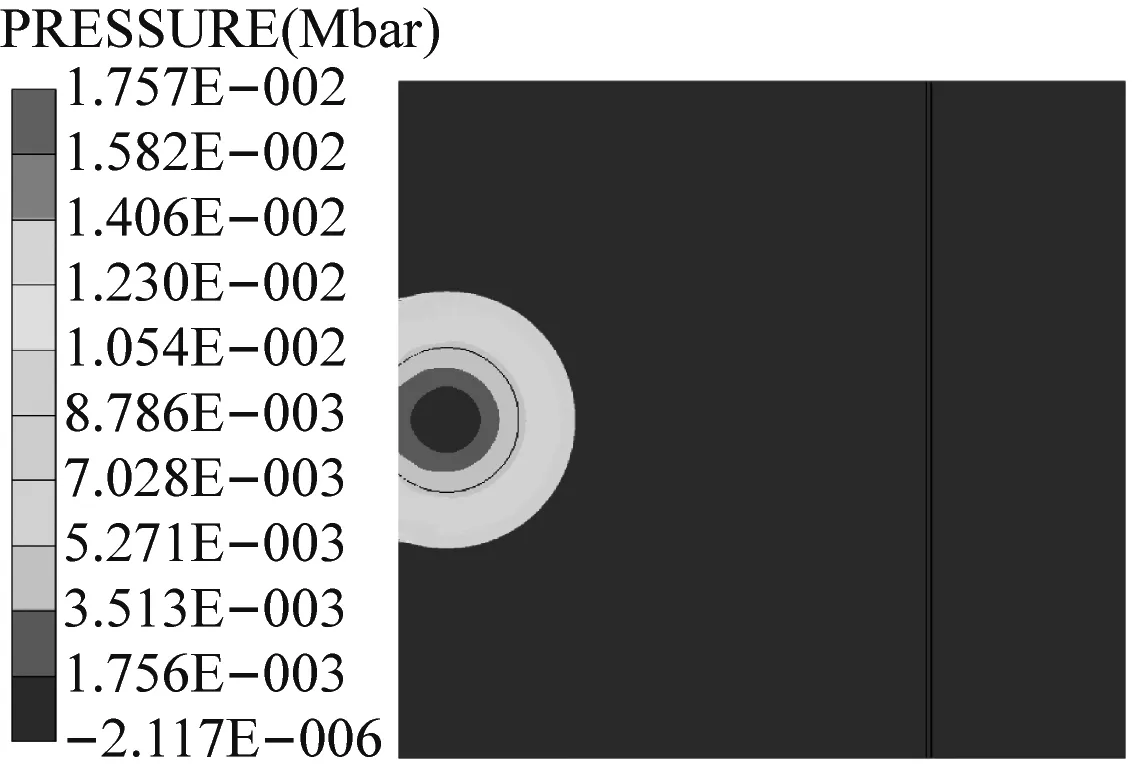
(a) t=70 μs

(b) t=200 μs

(c) t=460 μs

(d) t=580 μs

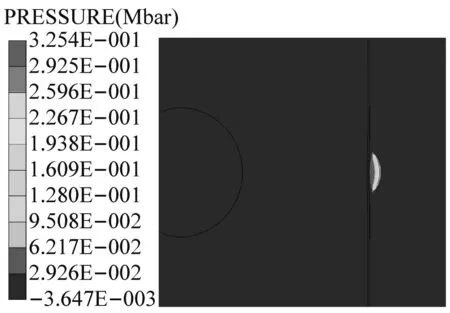
(e) t=720 μs

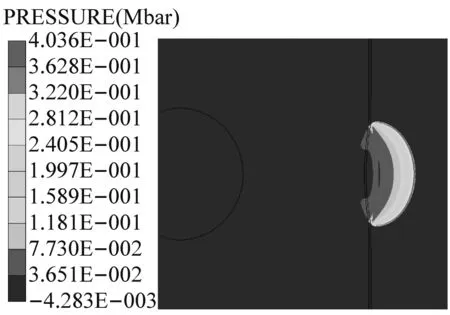
(f) t=740 μs

图4 不同时刻冲击波压力云图

Fig.4 Different time pressure shock wave cloud

图5为挡板附近不同位置的压力时程曲线，以水与挡板接触面为z=0，从图5可知，当冲击波传至挡板时，透射入挡板的压力有所提升，然后在挡板中传播又产生了一定的衰减，再次经过挡板与炸药分界面，透射入炸药的压力减小为95 MPa，与理论计算值相差2.92%，经过一段时间的作用，压力值有了明显的升高，说明此时炸药被引爆。

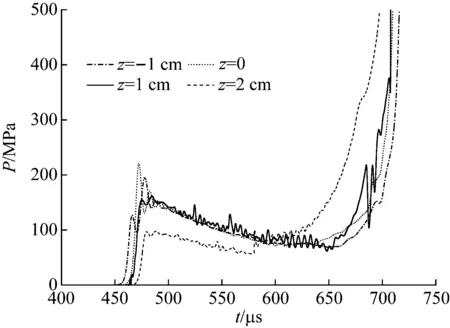
图5 挡板附近不同位置的压力时程曲线

3.3 屏蔽装药冲击引爆影响因素分析

随着主发药包与挡板之间距离的增加，到达挡板的冲击波强度逐渐减弱。采用“升—降法”调整此距离可知，在6.6 kg TNT药量下，主发药包在距挡板1.6 m处产生的冲击波不足以起爆被发药，冲击波在被发药中逐渐衰减，在持续时间内达不到临界引爆乘积要求。

在相同条件下调整挡板厚度，从仿真结果可知，随着挡板厚度的增加，透射入炸药的冲击波强度有所减弱，起爆时间逐渐延长，但引爆乘积变化不大。通过理论判据可以计算出不同屏蔽挡板厚度下，PBX-9404装药的临界起爆距离，图6给出了临界起爆距离随挡板厚度的变化曲线，从图中可以看出，随着挡板厚度的增加，由于透射入炸药的压力减小，炸药的临界起爆距离随之减小。通过理论计算模型可知，在挡板厚度一定的情况下，不同主发药量所能引爆屏蔽装药的临界距离不同，图7给出了临界起爆距离随主发药量的变化曲线。从图7可知，随着主发药量的增加，临界起爆距离逐渐增加。

由于透射入炸药的压力并不能达到临界起爆压力，炸药在低压力冲击波作用下经过相对较长的时间才起爆，因此采用第二种形式的冲击引爆判据pnτ=K，通过参数n、K来描述装药的起爆特性。利用表3中的数据，通过最小二乘方法拟合得到n=1.37，K=2.33×107(国际单位制)，与文献[9]中PBX-9404炸药的冲击引爆判据进行比较如图8，两者符合较好，在180～390 MPa内误差不超过15%。因此，利用理论简化模型以及拟合得到的冲击起爆判据公式，可以在一定范围内很好的描述屏蔽炸药在水下爆炸冲击波作用下的起爆特性。

图6 临界起爆距离随挡板厚度变化曲线

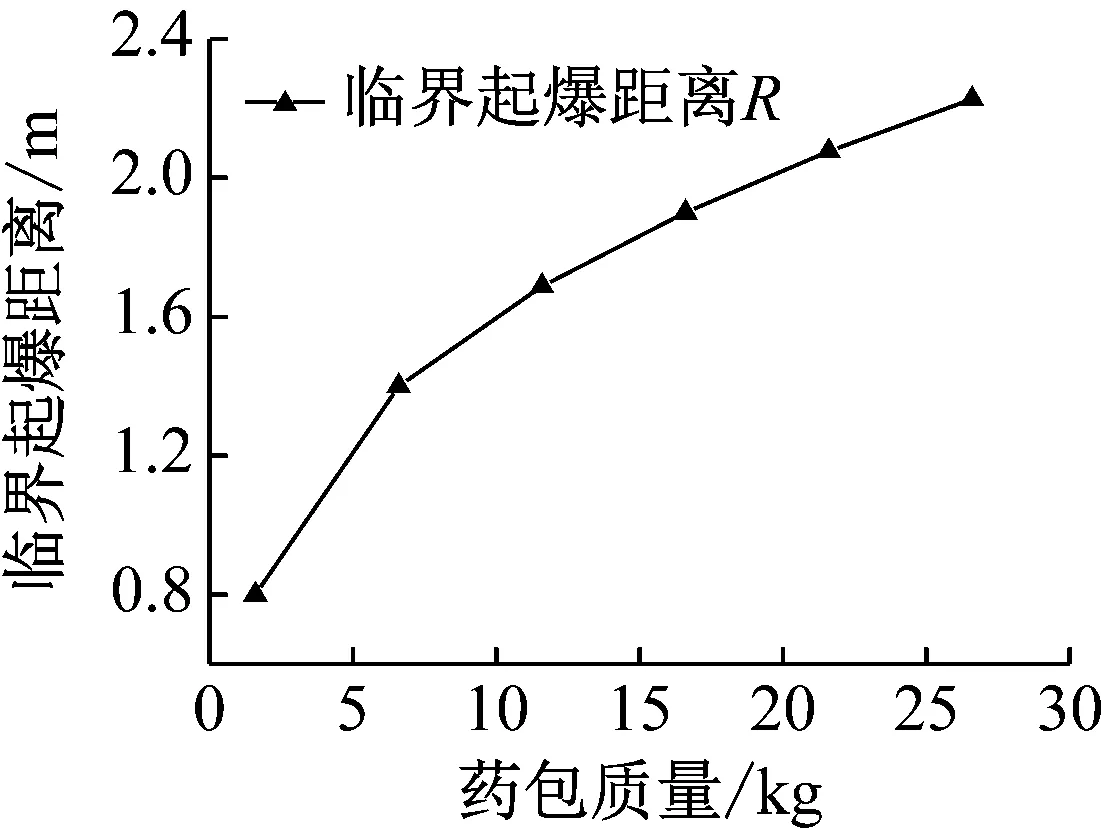
图7 临界起爆距离随主发药量变化曲线

图8 拟合曲线与经验曲线对比图

4 结 论

本文建立了水下爆炸冲击波对屏蔽装药的冲击压力计算方法，并利用AUTODYN软件对所建立的理论计算模型进行了验证。对不同爆距、不同挡板厚度的爆炸冲击波冲击引爆屏蔽装药的过程进行了数值模拟，并与理论结果进行对比，得出以下结论：

(1)数值模拟结果与理论计算结果最大误差为6.75%，吻合较好，说明建立的理论计算模型是有效的。

(2)相同条件下，随着爆距的增加，透射入炸药的冲击波压力逐渐减小，引爆装药的作用时间逐渐增长；在6.6 kg TNT装药量下，临界起爆距离约为1.6 m；随着屏蔽挡板厚度的增加，透射入装药的冲击波压力逐渐减小，炸药的临界起爆距离随之减小；随着主发药量的增加，临界起爆距离逐渐增加。

(3)通过最小二乘法得到了简化理论模型计算临界起爆判据的参数n、K，使得理论模型可以更好地描述屏蔽炸药在水下爆炸冲击波作用下的起爆特性，为冲击起爆实验研究和后续的可靠性研究提供一定的理论参考。