多人Bounce荷载下结构动力响应折减系数研究

陈 隽， 任静雅， 王 磊

(1. 同济大学 建筑工程系，上海 200092；2. 同济大学 土木工程防灾国家重点实验室，上海 200092)

伴随新型城镇化的国家发展战略，近年来体育场馆、展览馆、综合文化中心等文体公共建筑大量兴建，这些建筑物的共性特点是拥有大跨度、开敞式的楼盖/看台等结构，由于其频率低、阻尼小，在人群(观众)的走动、跳跃以及Bounce等荷载作用下会产生振动，此类振动称为人致结构振动[1-2]。

Bounce指人双脚不离开支撑面的身体上下往复运动，常见于体育比赛或演唱会中观众的庆祝动作，其对支撑面的作用称为Bounce荷载[3]。由于Bounce运动常见于群体性场合，且往往伴随有外部音乐、口号等因素的引导，极容易形成人群的协同性运动，当运动频率接近支撑结构频率时，共振效应会引起结构的显著振动，幅值过大则可能导致振动舒适度问题，严重时甚至会因人群的恐慌而诱发群体公共安全事故[4-5]。由于实验技术上的困难，此前对Bounce荷载特性与建模的研究主要集中于单人情况[6-8]，在此基础上通过引入假定研究人群荷载特性。例如，Parkhouse等在单人Bounce荷载实验的基础上，通过对齐节拍器时刻后叠加单人荷载的方式研究了人群Bounce荷载的特性，并提出了人数为特定值(5、10、20、50、100、200人)时的人群Bounce的动力因子值[9]。单人和人群荷载的本质差别在于协同性，即人群中各单人保持动作一致性的程度。上述将单人荷载强制对齐的处理方式，本质上忽略了人群中各单人间的相互影响这一关键要素。因此，利用同步实验研究人群Bounce荷载下的结构动力响应的分析方法有重要的实用价值和意义。

本研究将考虑和不考虑Bounce人群协同性所计算得到的结构响应比值定义为折减系数，将其与单人Bounce荷载下结构动力响应的反应谱计算方法相结合，以实现人群Bounce荷载下结构响应的快速计算。首先利用英国谢菲尔德大学15人同步Bounce实验数据，研究了各种要素对折减系数的影响，并建立了响应折减系数的经验公式。

1 多人同步Bounce荷载实验

多人同步Bounce实验是荷载特性及对结构响应影响研究的必要前提和重要的数据基础。由于实验设备与人数之间的矛盾，人群同步Bounce实测数据非常少，有学者使用三维动作捕捉技术[10]和计算机视觉识别技术[11]间接进行研究。本研究中的多人同步Bounce时程实测数据由谢菲尔德大学Racic博士提供，该实验通过一个模拟体育看台的装置进行[12](如图1)。

图1 模拟体育看台

该模拟看台有3排，每排有5个座位，看台坡度为21°，座椅间距为前后1.0 m、左右0.5 m，严格按照实际体育看台布置。模拟看台使用轻质刚性材料，以使自振频率远大于人群可达到的同步Bounce频率，保证测试过程中不激发模拟看台的内部振动模态。每个座位前安装了测力板，采样频率为1 000 Hz，用来同时收集15位测试者各自的足底反力。

实验共采集了1.5、2.0、2.5以及3.0 Hz四种频率下的15人(平均体重720.4 N)同步Bounce荷载时程，每个工况测试持续40 s左右，采样频率为1 000 Hz。各频率下的名义荷载(实测荷载/体重)时程曲线及相应的傅里叶幅值谱如图 2所示，其中细线为每位测试者的名义荷载时程，粗线为15人的平均名义荷载时程。

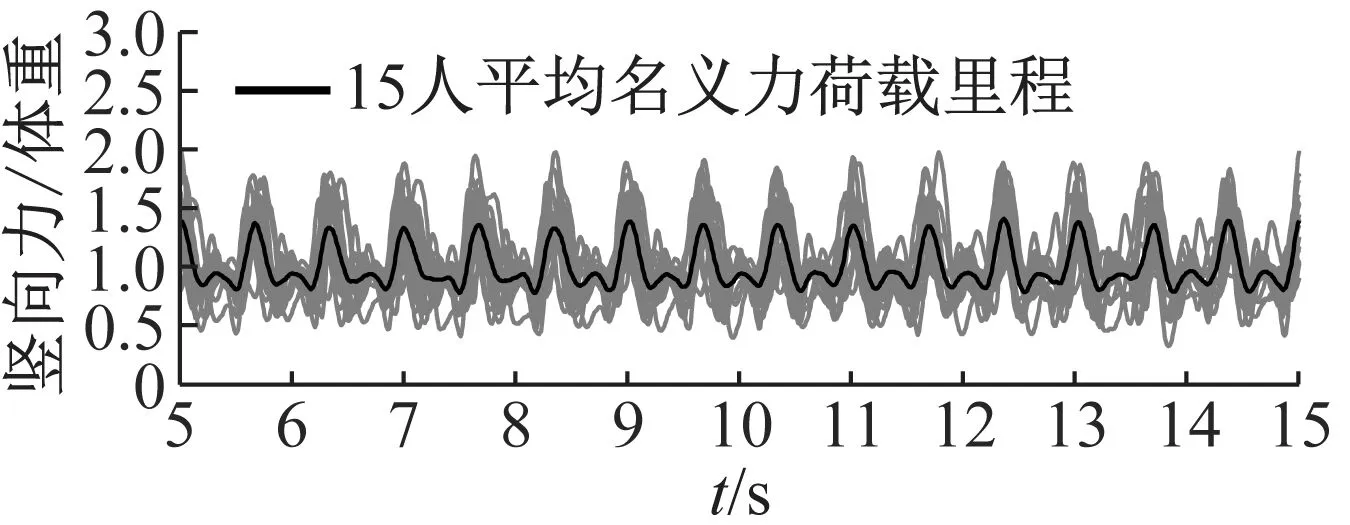
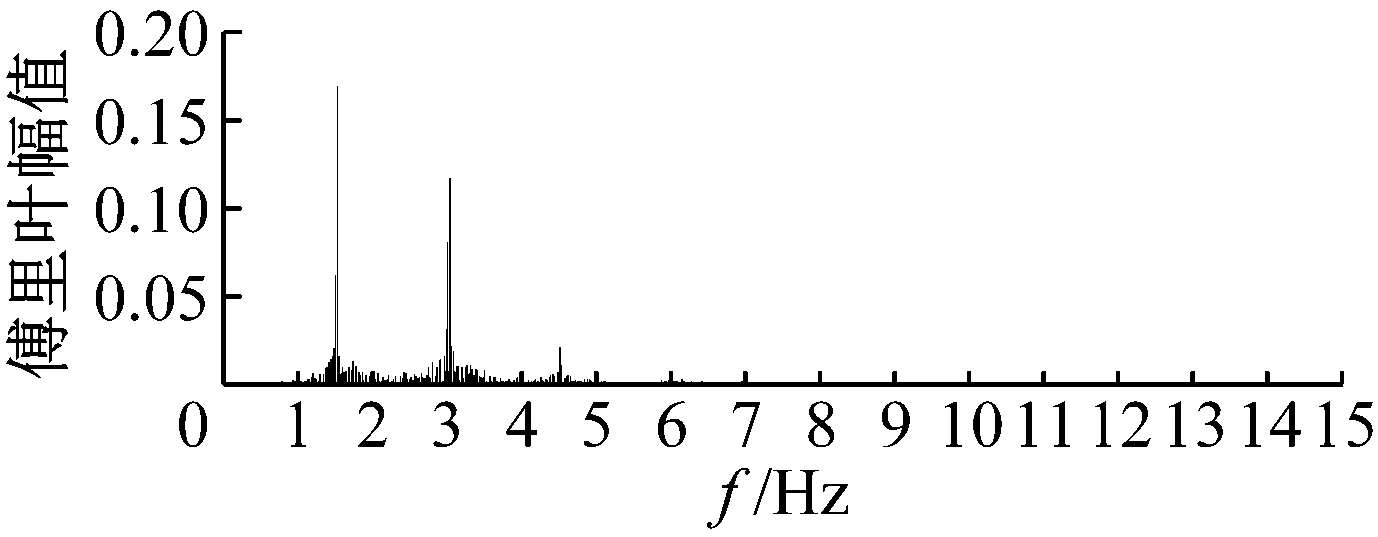
(a) 1.5 Hz Bounce荷载时程及其幅值谱

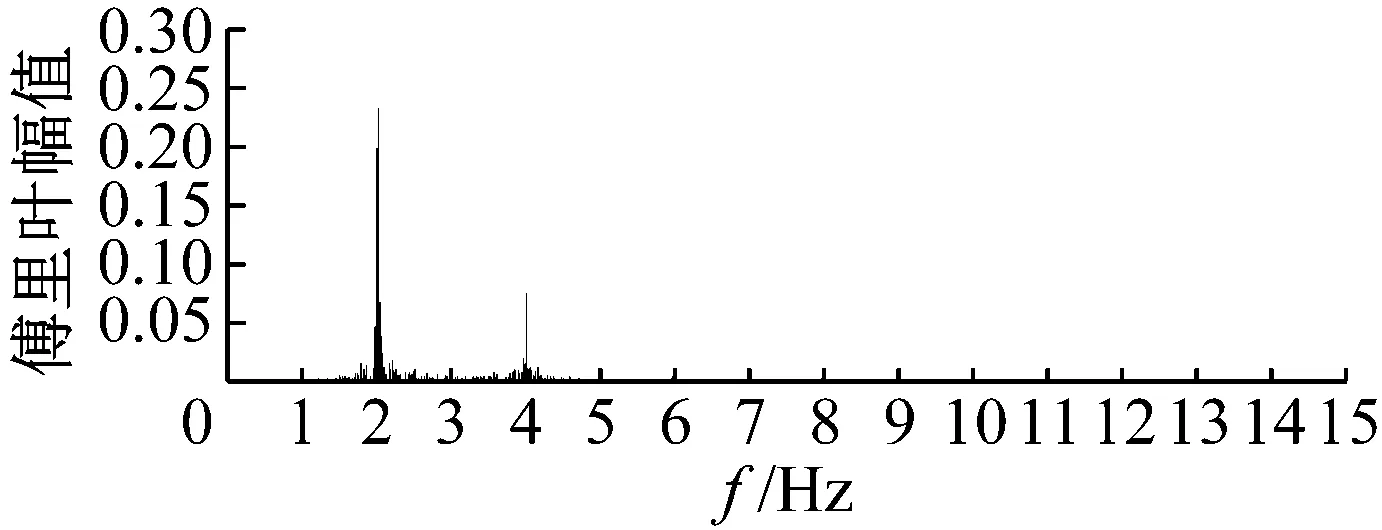
(b) 2.0 Hz Bounce荷载时程及其幅值谱

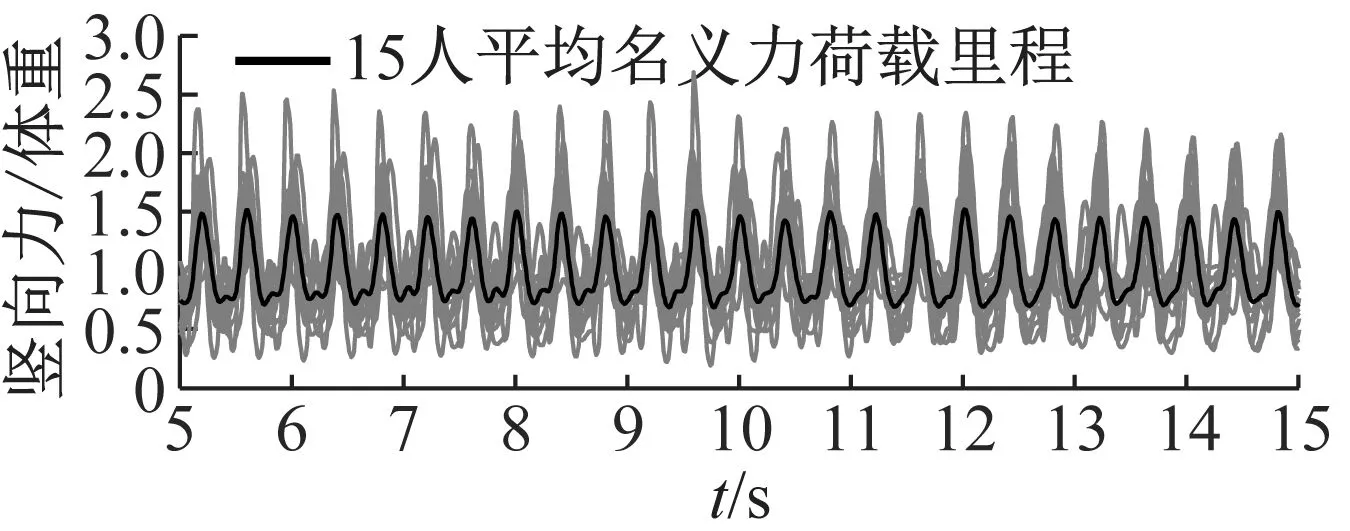
(c) 2.5 Hz Bounce荷载时程及其幅值谱

(d) 3.0 Hz Bounce荷载时程及其幅值谱

2 多人Bounce结构动力响应折减系数

2.1 动力响应折减系数的定义

从工程应用的角度，单人Bounce荷载及对应的结构响应计算已有相对成熟的模型和方法[13]。由于人群中各单人的协同性差异，所引起的结构响应小于单人响应与人数的乘积。通过引入多人Bounce下结构动力响应折减系数，可实现由单人到人群的结构响应快速计算。由于Bounce荷载的窄带特性[14](图 2)，结构响应通常由单一模态控制，参考图 3可定义如下的响应折减系数

(1)

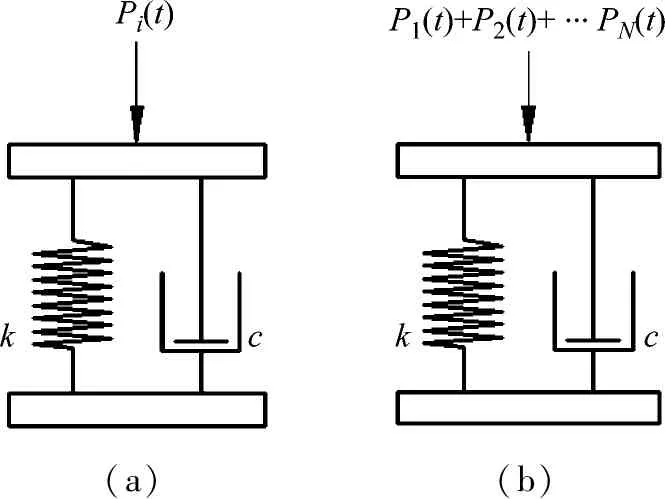
(a)(b)

图3 单自由度结构的荷载输入模拟

Fig.3 Load input simulation of single degree of freedom structure

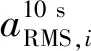
2.2 响应折减系数谱

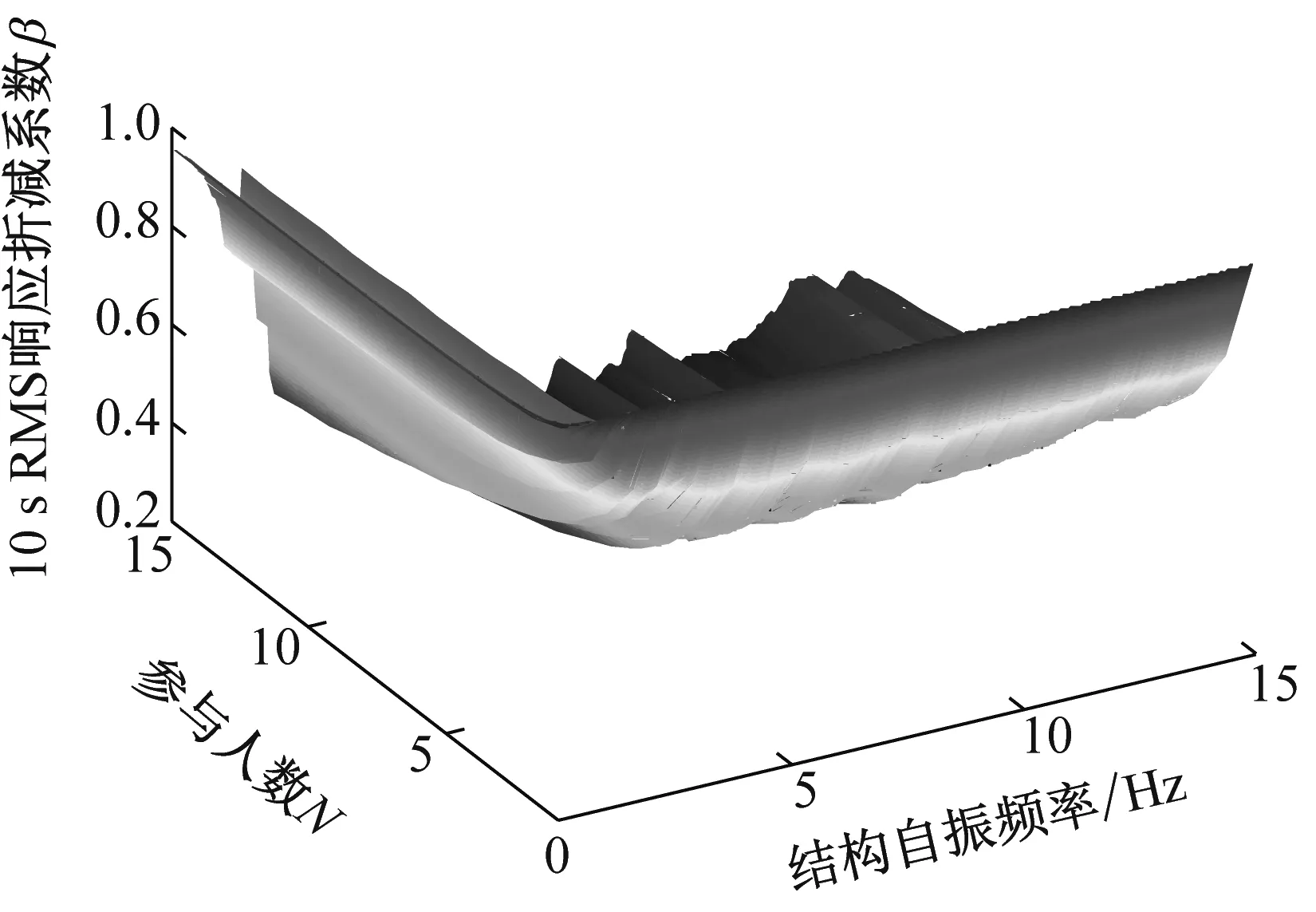
(a) 1.5 Hz Bounce

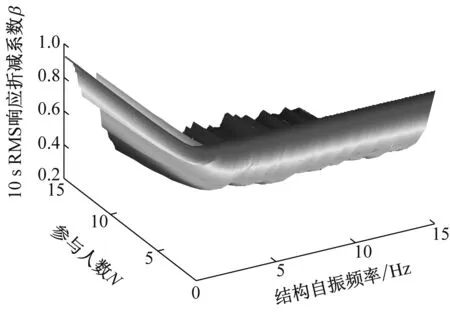
(b) 2.0 Hz Bounce

(c) 2.5 Hz Bounce

(d) 3.0 Hz Bounce

图4 响应折减系数与人数和结构频率的关系(阻尼比：2%)

Fig.4 Relationship between response reduction factor and crowd size and structure’s natural frequency (damping ratio 0.02)

从图4可以看出，给定结构频率时，随着人数N的增加，折减系数呈降低趋势并逐步稳定，因此可偏保守地用15人的结果代表人群。图5给出了四种Bounce频率下N=15时折减系数β随结构频率变化曲线。从图中可以看出，不同Bounce频率下β的变化趋势大致相同，数值差别不大，从方便使用的角度，取四种频率的均值曲线作为阻尼比为2%时的代表曲线，即图5中粗线。

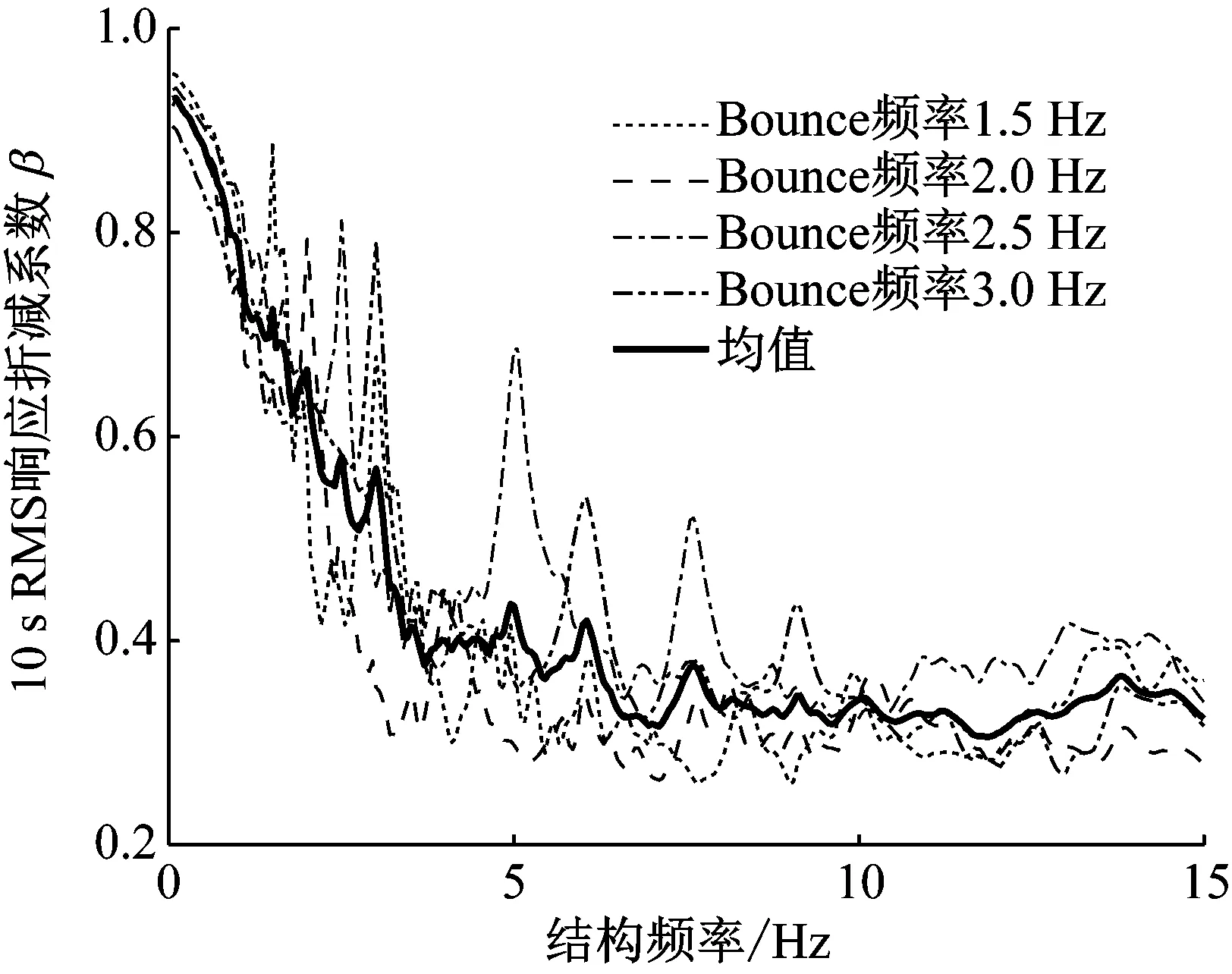
图5 15人Bounce时响应折减系数曲线(阻尼比：2%)

按照相同步骤，计算了其它阻尼比下折减系数代表曲线，结果见图6。从图中可见，结构阻尼对人群Bounce时的响应折减系数曲线整体趋势的影响不大。但对曲线形状有一定影响，由于阻尼比越大时，结构响应衰减越快，结构自振频率对响应折减系数的影响越小，因此阻尼比越大，曲线的形状越光滑。

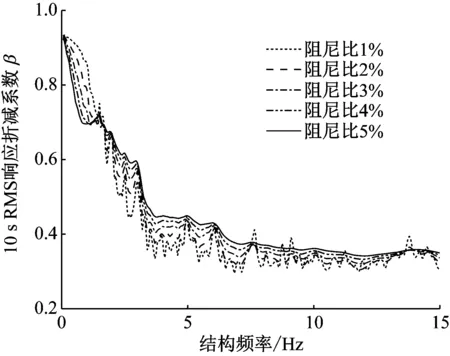
图6 不同阻尼比下的响应折减系数均值曲线

以上5条曲线求均值，得到10 s均方根加速度折减系数曲线的代表曲线，将其与全长均方根、峰值加速度折减系数代表曲线对比，如图7。可发现三条曲线的形状、趋势及数值大小并无太大区别，为方便使用，确定响应折减系数曲线时，可忽略不同计算指标的差异。

对三种指标响应折减系数曲线的均值进行最小二乘拟合，可得响应折减系数设计曲线和设计表达式，见图8和式(2)。

β=0.325+0.602e-0.381f

(2)

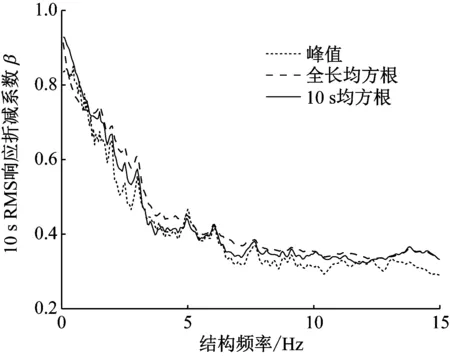
图7 三种指标下的响应折减系数代表曲线

图8 响应折减系数的设计曲线

3 折减系数曲线的应用

3.1 单人Bounce荷载下结构响应的反应谱法

基于大量的单人Bounce荷载实测值，作者在文献[13]中提出了单人Bounce荷载下结构响应的反应谱计算方法。该方法采用图9所示设计反应谱曲线，对应公式见式(3)。设计曲线使用类比于地震反应谱的方法，可获得单人Bounce荷载下结构的最大加速度反应，具体步骤见文献[13]。

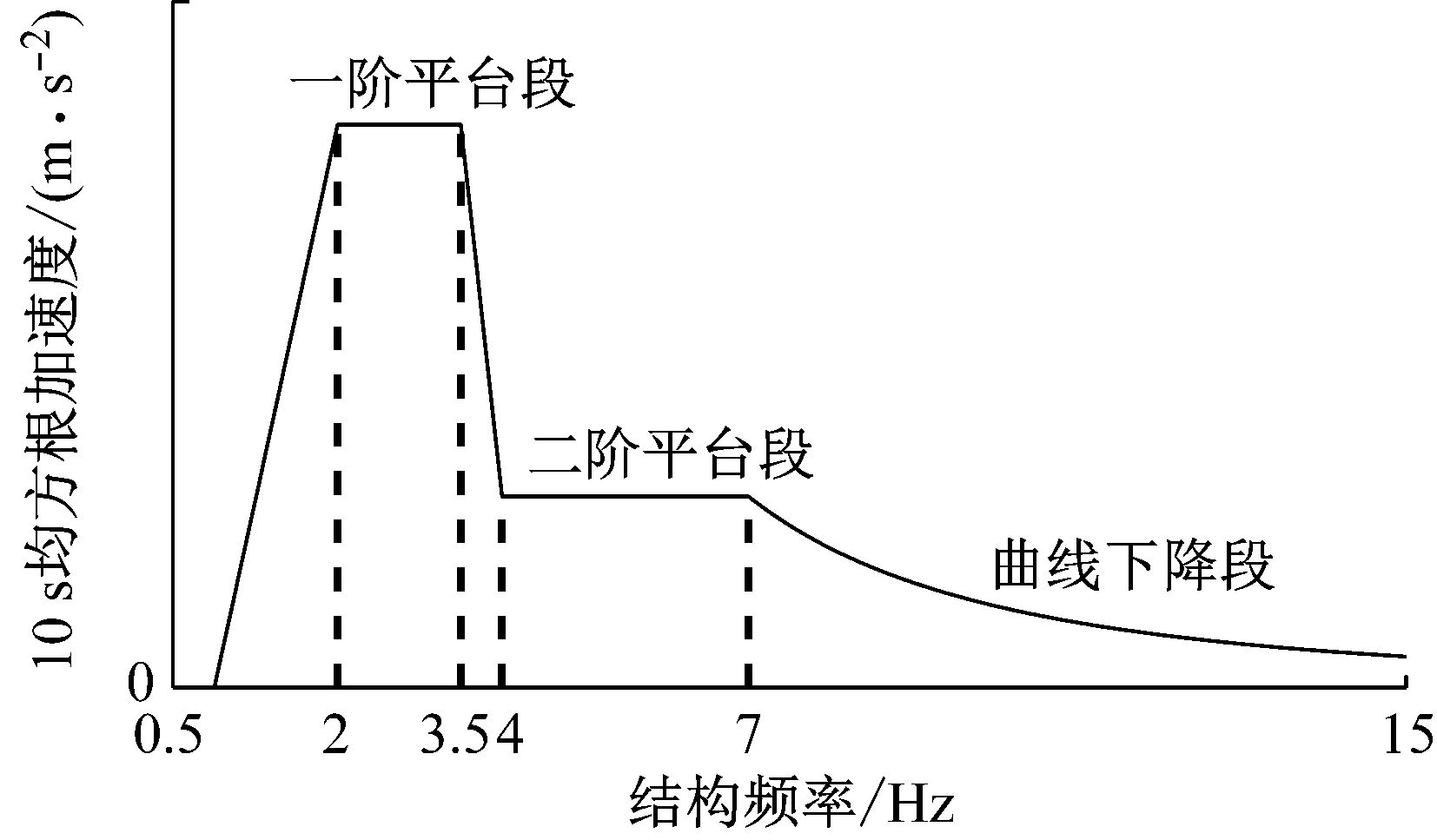
图9 单人Bounce荷载下设计反应谱曲线

a(f,ζ,P)=

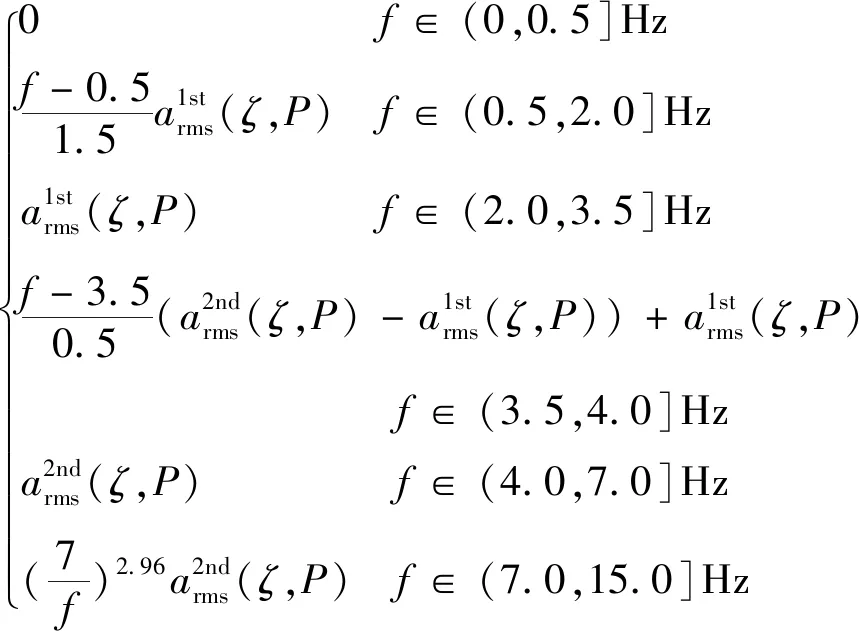
(3)

3.2 基于折减系数的多人Bounce下结构响应分析

以楼板结构为例，图10(a)是多人Bounce作用的示意图，对于人群荷载以离散点(总人数N已知)或分布形式(单位面积上人数已知)两种方式施加于结构时，结合反应谱法和动力折减系数的结构响应计算公式为

(4)

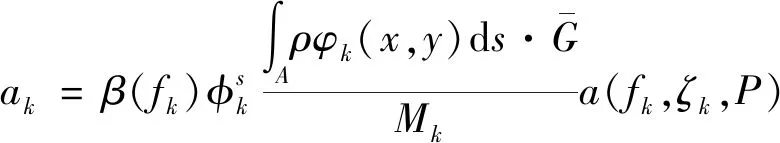
(5)

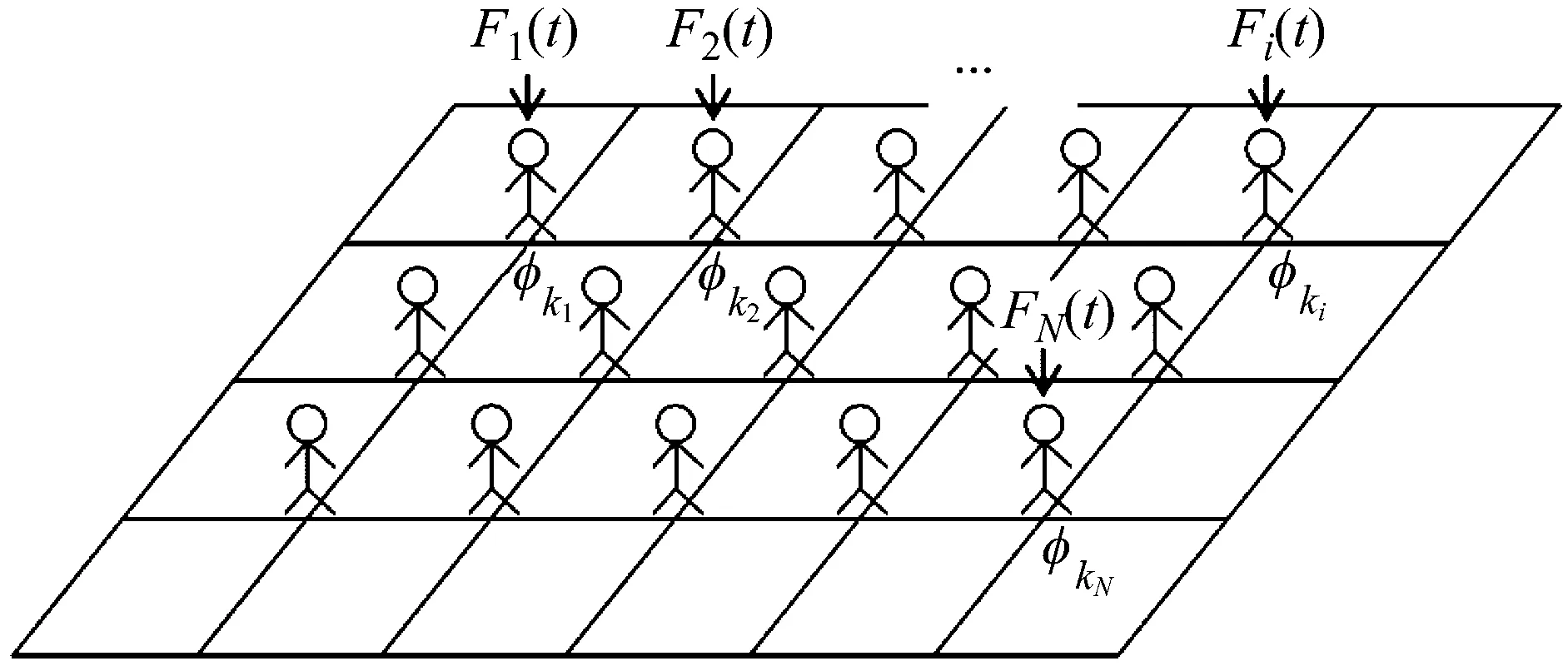
图10 多人Bounce的荷载施加

至此，多人Bounce下楼盖的动力响应分析可按如下三个步骤进行：

步骤1 运用有限元方法或实测获得楼盖各阶振型的频率、阻尼比、振型以及模态质量。由于高阶振型对响应影响较小，可仅考虑振型频率小于15 Hz的各阶模态。对于人数较多的情况，可取较大的结构阻尼值以考虑人-结相互作用的影响。

步骤2 确定所选取的分位数P(如0.95，0.75等)，然后按式(4)或式(5)计算第k阶振型对应的多人Bounce下楼盖结构10 s均方根加速度响应：

步骤3 对步骤2中的各阶加速度响应求其最大值，并以其作为楼盖的加速度响应预测值。

4 算例分析

建立图11所示四边简支混凝土方板模型，将实测的2.5 Hz人群Bounce荷载施加于模型上，考虑到人群有增大结构阻尼的作用[15]，取各阶阻尼比5%，由时程分析可得到板中心的加速度响应(图12)，最大10 s均方根加速度为2.48 m/s2。

此外，按照上节所述步骤对板中心响应进行计算，具体计算参数和步骤见表2。取P=0.75时，计算值为2.84 m/s2，略大于有限元分析结果。对其它荷载工况也进行了计算对比，结果显示采用P=0.75时，折减系数法获得的结果与有限元法接近，可用于人群Bounce下楼板响应的快速预测。

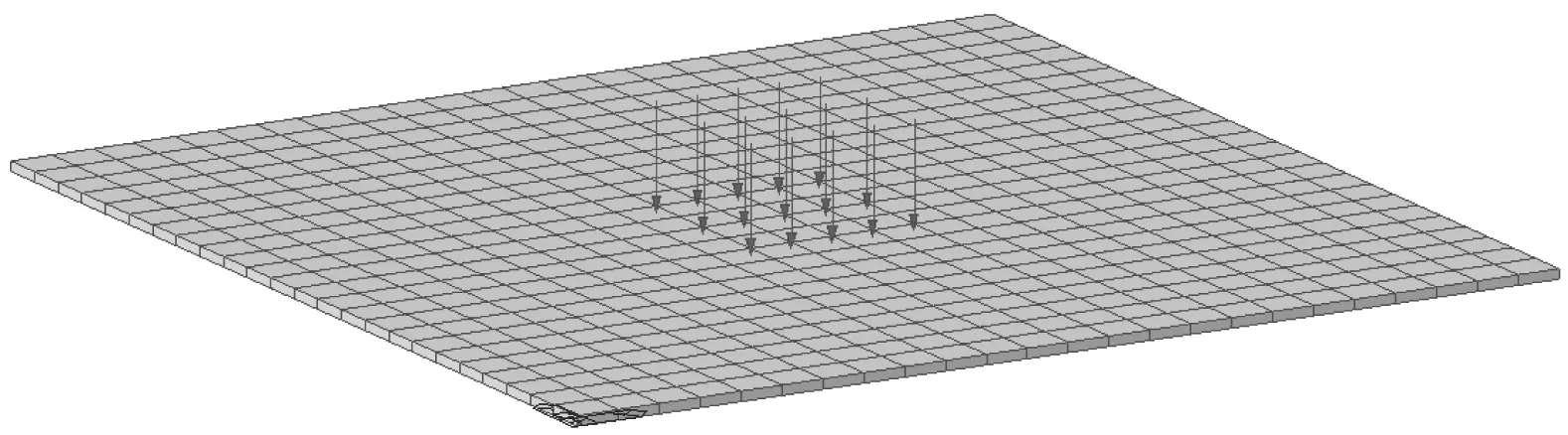
(a) 多人Bounce荷载在有限元模型中的施加

(b) 荷载施加点的布置

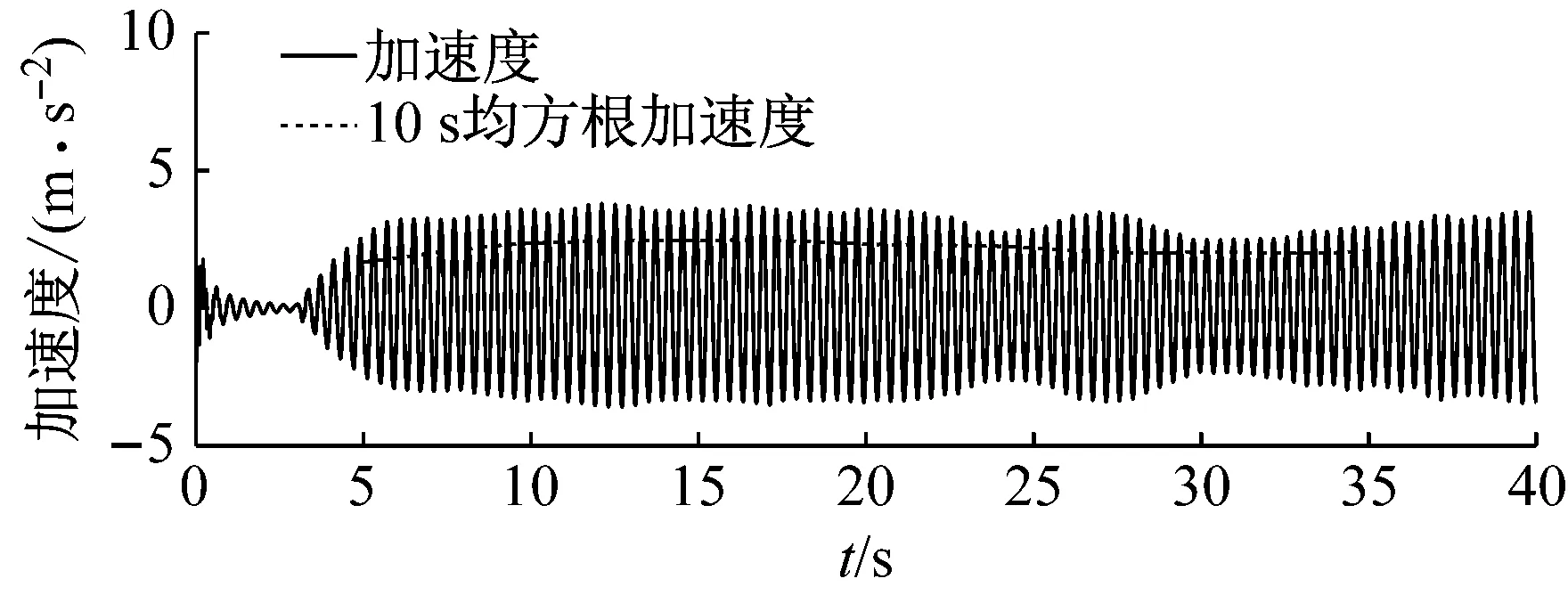
图12 算例板中心加速度响应时程

表2 多人Bounce下加速度响应计算步骤

5 结 论

本文以多人同时Bounce实验数据为基础，提出了多人Bounce下的响应折减系数，并研究分析了人数、结构频率、结构阻尼比以及Bounce工况频率对折减系数的影响。通过对各典型阻尼比折减系数代表曲线拟合得到了响应折减系数设计曲线，与单人Bounce下结构响应的反应谱方法相结合，可以实现对楼板等结构在人群Bounce荷载作用下响应的快速预测，算例分析表明了所建议的折减系数和计算方法的可行性。

由于实验人数与频率的限制，文中所提出的折减系数只适用于人群人数大于15人且Bounce频率在1.5～3.0 Hz之间的情形。同时折减系数推导时未考虑人结相互作用的效应。由上述两个因素使得对于人数较多的场合，采用折减系数法可能高估结构的响应。因此建议对于N>50的情况，可适当调高结构阻尼比以综合反映人结相互作用及N>15对减少结构响应的有利影响。