自适应TQWT滤波器算法及其在冲击特征提取中的应用

孔 运， 王天杨， 褚福磊

(清华大学 机械工程系，北京 100084)

机械故障特征提取与信号处理，是机电设备状态监测与故障诊断的核心技术，是保障重大高端设备高效可靠安全服役的关键。实现强背景噪声干扰下的微弱故障冲击特征提取，对于核心部件的早期故障诊断至关重要。

小波分析，作为数十年来信号处理技术在机械故障诊断领域的研究热点之一[1]，被广泛应用于早期微弱故障特征提取。小波变换本质上是基于内积变换原理的特征波形基函数与故障特征相似性匹配，与故障特征波形局部最相似或最相关的小波基函数能够最佳地表征多源噪声干扰下的早期故障特征信息[2-3]。

有效地构造并优化与故障特征波形相匹配的小波基函数，使得小波分析在微弱故障特征提取与降噪方面取得了长足进步。在连续小波变换方面，Lin等[4]通过最小化小波熵对Morlet小波基函数的波形参数进行优化，实现了早期微弱故障的特征提取。Jiang等[5]进一步同时优化Morlet小波的带宽与中心频率参数，并选择合适的小波尺度实现与冲击故障特征的自适应匹配。Wang等[6]通过对瞬态特征建模，并利用相关滤波识别瞬态信号模型参数，实现微弱故障瞬态特征提取。

相比于上述直接从时域上构造并优化小波基函数的经典方法，从频域上构造小波的理论正在迅速发展[7-10]。其中，由Selesnick提出的可调品质因子小波变换(TunableQ-factor Wavelet Transform, TQWT)，作为一种新兴的从频域上构造小波的过完备式小波变换，其显著优点是可通过指定品质因子、冗余度以及分解层数三个关键的TQWT参数，使可调品质因子小波对具有特定振荡行为的特征信号成分实现最优匹配，并且能够利用FFT算法快速实现。故障特征波形，本质上也可视为具有特定衰减振荡行为的特征成分，因而TQWT能够适用于微弱故障瞬态特征提取，正逐步受到学者们的关注。Luo等[11]利用TQWT分解轴承振动信号，并利用峭度指标选择故障特征频带解调分析，实现轴承故障检测。He等[12]研究了TQWT与相邻系数降噪方法相结合对振动信号的降噪效果，并根据Hilbert解调谱提出故障特征比对可调品质因子小波进行优选，用于轴承微弱故障的检测[13]。Zhang等[14]基于TQWT构造冗余小波字典，提出了峭度加权的稀疏模型并用于轴承故障信息的稀疏表示。

针对强背景噪声下微弱冲击故障特征提取，本文提出参数自适应选择的TQWT滤波器算法。该算法的目的是提出一种TQWT关键参数以及最优特征子带的自适应选择策略，提取轴承局部损伤诱发的周期性非平稳微弱冲击特征。首先利用TQWT分解含局部损伤的机械动态信号，然后结合所提出的中心频率比指标以及基于能量加权归一化小波熵指标的优化准则引导TQWT关键参数的选择。整体来看，通过遍历具有不同振荡特性的可调品质因子小波对故障特征表达的稀疏性程度，从非单一固定的小波基函数库中优化筛选出适合故障特征信息表达的最佳可调品质因子小波基函数，并由冲击特征指标引导最优特征子带选择，进而实现降噪信号的重构，提取出周期性微弱冲击特征。将所提出的自适应TQWT滤波器算法，应用于滚动轴承的故障冲击提取，验证了方法的有效性。

1 可调品质因子小波变换理论

品质因子作为衡量小波振荡行为的重要性能参数，其选择决定着小波基函数与信号特征分量的相似性度量，进而影响小波变换特征提取的效果。因而，利用小波变换分析特定振荡行为的信号时，小波品质因子的可调控性质十分重要。现有除连续小波变换外的绝大多数小波变换，不能实现品质因子的调控。TQWT作为一种新兴的品质因子可调控的过完备式离散小波变换，通过选取合适品质因子、冗余度以及分解层数三个TQWT参数，可使可调品质因子小波对特定振荡行为的特征信号成分实现最优匹配。此外，相比于从时域上构造小波基的传统连续小波变换，TQWT的设计由频域显式构造，具有可利用基2-FFT算法快速实现的优点。因此，TQWT在微弱故障瞬态特征信号(可视为较低振荡行为的特征信号分量)的提取上，具有重要应用前景。

1.1 TQWT基本记号

TQWT作为频域显式构造小波的新兴理论，信号的频域表示采用单位离散傅里叶变换(Unitary Discrete Fourier Transform, uDFT)。对于长度为N的离散信号x(n)，uDFT及其逆变换uDFTI分别定义为

X(k)=uDFT{x(n)}⟹

0≤k≤N-1

(1)

x(n)=uDFTI{X(k)}⟹

(2)

式中：i为虚数基本单位。

本质上讲，TQWT通过单位离散傅里叶变换获取输入信号的频域表示，并设计特定尺度变换系数下的过采样滤波器组，在频域上实现小波分解与重构，具备完美重构的性质。如图1(a)所示，TQWT分解由一系列迭代双通道滤波器组构成，通过对低尺度下滤波器组的低通输出不断进行高、低通滤波器迭代分解，得到多尺度TQWT分解的小波系数序列{W(j)(n)}，j=1,2,…,J+1。其中，H0(ω)与H1(ω)分别为低通与高通滤波器频响函数，α与β分别为低通尺度变换LPS与高通尺度变换HPS的尺度变换系数。

1.2 TQWT基本滤波器组

TQWT基本滤波器组的低、高通滤波以及低、高通尺度变换，均从频域上设计与实现。为保证TQWT完美重构的性质，低、高通尺度变换系数α与β需满足约束

(a) TQTW信号分解过程

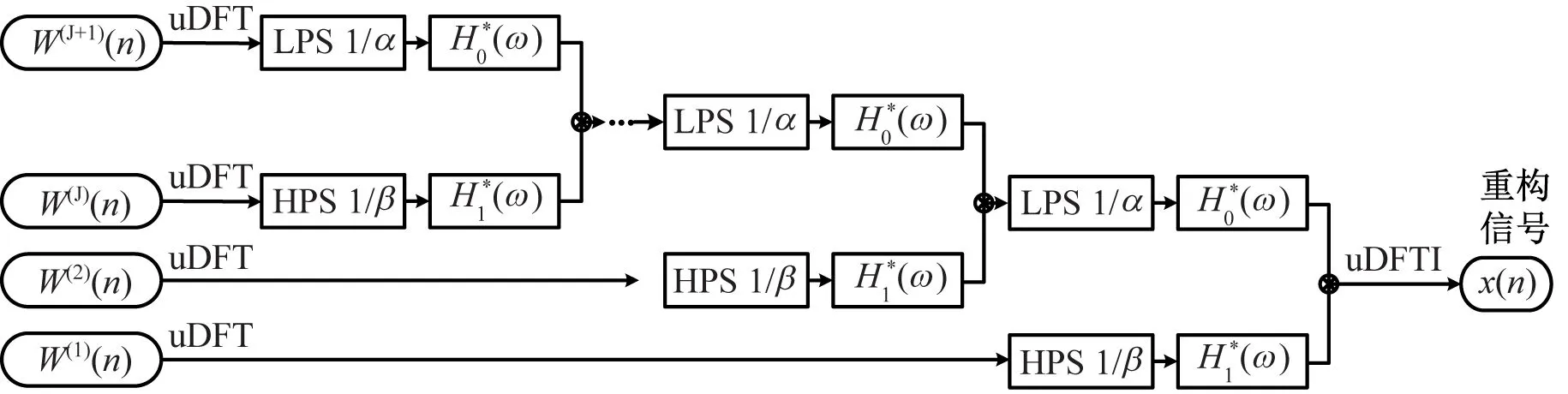
(b) TQTW信号重构过程

0<α<1, 0<β≤1,α+β>1

(3)

TQWT的完美重构特性，要求低、高通滤波器频响函数H0(ω)与H1(ω)在各自的通带以及过渡带上均满足重构条件，即H02(ω)+H12(ω)=1。具有二阶消失矩的Daubechies频响函数θ(ω)满足2π-功率互补特性，可表示为

θ2(ω)+θ2(π-ω)=1

(4)

(5)

利用Daubechies频响函数θ(ω)规范低、高通滤波器频响函数H0(ω)与H1(ω)的过渡带频响特性，可满足完美重构条件，具体定义如下

H0(ω)=

(6)

H1(ω)=

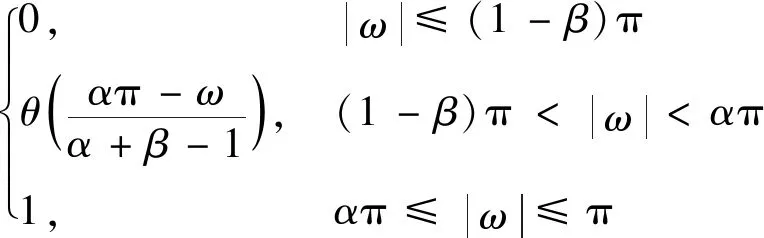
(7)

类似地，低、高通尺度变换LPSα与HPSβ表示频域下尺度变换，分别保留输入信号的低频与高频成分。

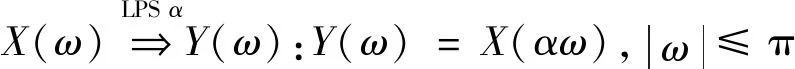
(8)

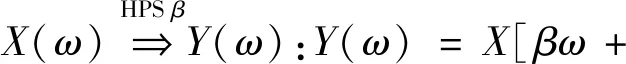
sign(ω)(1-β)π]

(9)

式中：sign(·)为符号函数。

1.3 TQWT多尺度分解下的等效滤波器

根据高低通滤波及其后续相应高低通尺度变换的频域性质，结合TQWT多尺度分解下基本滤波器组的迭代操作，可以得到TQWT小波系数序列{W(j)(n)}与输入信号x(n)之间的频率响应特性。图2所示为分解层数为j时，TQWT多尺度分解下高通与低通输出的等价滤波器操作，其中C(j)(n)与W(j)(n)分别为低通与高通输出。

(a) 低通输出等效滤波器

(b) 高通输出等效滤波器

TQWT多尺度分解下的等效滤波器频响特性可表示为

(10)

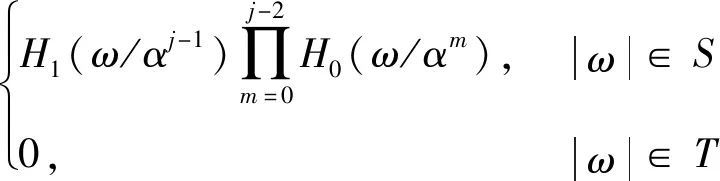
(11)

式中：S与T为关于ω的区间，S=[(1-β)αj-1π,αj-1π],T=[-π, π]/S。

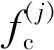
(12)

式中：fs为输入信号的采样频率。

对于TQWT而言，尺度变换系数α与β决定了TQWT所有尺度下小波的时域以及频域特性，其取值由TQWT参数品质因子Q与冗余度参数r确定

(13)

因此，TQWT时域与频域特性由三元参数组合P=(Q,r,J)唯一决定，其中J为分解层数。

2 自适应TQWT滤波器算法

TQWT三元参数组合P决定了可调品质因子小波与待分析信号特征分量的相似性匹配，其选择在微弱故障特征提取与降噪中扮演重要角色。通过分析实测机械动态信号，自适应选择适合微弱故障冲击特征表征的TQWT参数，并选取故障特征对应的最优子带进行信号重构与降噪，对早期微弱故障特征提取具有重要意义。作者称此过程为自适应TQWT滤波器算法，由自适应可调品质因子小波构造以及最优特征子带选择组成。

2.1 自适应可调品质因子小波构造

可调品质因子小波的构造主要取决于品质因子与冗余度(Q,r)的选择，分解层数的选择仅仅影响着TQWT在低频区域的频域分解性能。过多的分解层数将引入过高的计算成本，同时可能导致对故障特征频带信息的过度分解或故障无关频带信息的冗余分解。鉴于局部故障对应故障特征频带往往位于较高的频率区域，合理的分解层数既应涵盖足够宽的频域范围来覆盖故障特征频域信息，又不能过大而引入高昂计算成本。

文献[8]中指出，对于给定品质因子Q与冗余度r，分解层数存在最大值Jmax，以保证Jmax尺度下的小波持续时间长度不超过所分析信号的时域范围

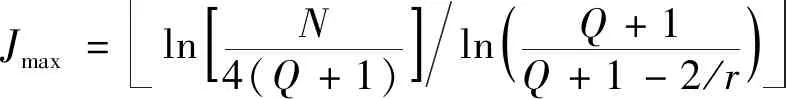
Jmax=lnN4(Q+1)[]lnQ+1Q+1-2/r()

(14)

式中：N为所分析离散信号x(n)的数据长度。本文提出基于中心频率比的合理分解层数确定准则，中心频率比(CFR)定义及合理分解层数停止准则表示如下

(15)

CFR(Q,r,J)≤T

(16)

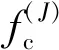
Ja=min(J,Jmax)

(17)

关键参数(Q,r)的优化选择，对TQWT小波基函数的自适应调控至关重要。已有研究表明，小波变换系数的稀疏性可以表征小波基函数与故障特征波形的匹配度，并且小波香农熵可用于评估连续小波变换所得小波系数的稀疏性。因此，学者们广泛地利用小波香农熵优化选择Morlet小波的中心频率与带宽参数。

但TQWT与传统连续小波变换存在重要差异：① 可调品质小波的能量依赖于尺度选择，而连续小波变换不同尺度下的小波具有恒定能量；② TQWT分解所得小波系数序列长度随着(Q,r)的调控不固定，而连续小波变换在尺度离散化以及时域采样频率确定的前提下，所得小波系数序列长度固定。

鉴于经典小波香农熵无法评估不同TQWT参数组合(Q,r,J)下长度相异小波分解系数序列的稀疏性，以及可调品质因子小波能量具有尺度依赖性，本文提出能量加权归一化小波熵优化选择TQWT参数(Q,r)的准则。三元参数组合(Q,r,J)下的能量加权归一化小波熵INE(Q,r,J)定义如下

(18)

(19)

INE(Q,r,J)=IE(Q,r,J)/max{IE(Q,r,J)}

(20)

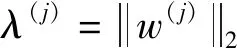
综上，针对P参数空间VP下特定的(Q,r,J)参数组合，构造自适应可调品质因子小波匹配冲击特征波形的步骤为

步骤1Q作为影响TQWT小波振荡特性的主要参数，r主要调节相邻尺度下小波频率响应的频域交叠以及计算成本。设定(Q,r)的二维参数网格空间

{(Q,r)|Q∈[QL:τQ:QU],r∈[rL:τr:rU]}

(21)

式中：{QL,QU,τQ}为品质因子的搜索上下边界与步长；{rL,rU,τr}为冗余度的搜索上下边界与步长。

步骤2 针对任一参数组合(Q,r)选取合理分解层数Ja。

步骤3 明确所有TQWT三元参数组合P=(Q,r,Ja)构成的参数空间VP。

步骤4 针对参数空间VP下的任一参数组合(Q,r,Ja)，对输入信号x(n)进行多尺度TQWT分解

W(J+1)(n)}

(22)

步骤5 利用能量加权归一化小波熵INE(Q,r,Ja)评估TQWT多尺度分解小波系数的稀疏性。

步骤6 监测和整合参数空间VP下INE(Q,r,Ja)的变化趋势，选择最小值对应的最优参数组合Popt=(Qopt,ropt,Ja)，构造自适应可调品质因子小波。

2.2 最优特征子带选择

构造自适应可调品质因子小波之后，可获得自适应TQWT多尺度分解的子带信号，选取恰当特征子带进行单支重构与降噪，可提取强噪声信号中的故障冲击特征信息。

已有研究表明，峭度可以作为评估信号冲击性的良好指标，但峭度值容易受到随机冲击噪声等因素的干扰，此时仅以峭度指标引导小波尺度的选择准则会降低小波降噪性能。鉴于平滑指标系数不易受随机冲击的干扰，同时也能衡量信号的冲击性，子带信号对应的平滑指标系数越小，其冲击性越突出[15-17]。本文通过子带信号峭度值与平滑指标系数的比值定义冲击特征指标，建立以冲击特征指标导引的最优特征子带选择准则。

(23)

(24)

KSR(j)=Kurt(j)/SI(j)

(25)

(26)

式中：μj与σj为尺度j下子带信号W(j)的均值与标准差；Kurt(j)、SI(j)以及KSR(j)分别为子带信号W(j)的峭度指标、平滑指标系数以及冲击特征指标；jopt为最大冲击特征指标对应的最优特征子带。

2.3 自适应TQWT滤波器算法流程

根据构造的自适应TQWT分解以及最优特征子带选择准则，提出自适应TQWT滤波器算法。算法可用于周期性微弱冲击特征提取，步骤为：

步骤1 对输入信号x(n)构造自适应可调品质因子小波，获取最优TQWT参数组合Popt=(Qopt,ropt,Ja)。

步骤2 根据冲击特征指标导引的最优特征子带选择准则，确定自适应TQWT分解的最优特征子带jopt。

步骤3 利用图1(b)所示的TQWT信号重构过程，对最优特征子带jopt进行单支重构，获取降噪信号。

步骤4 对降噪信号进行Hilbert包络解调，识别周期性故障冲击特征频率。

3 冲击特征提取仿真验证

为验证自适应TQWT滤波器算法在周期性微弱冲击特征提取中的有效性，现模拟一组采用式(27)构造的周期性冲击信号，其中幅值Am=1，衰减系数n=50，固有频率fn=200 Hz，首个冲击发生时刻T0=0.06 s，冲击周期Tf=0.2 s，u(t)为单位阶跃函数，为模拟实际工况中的随机噪声添加强高斯白噪声N(t)，信噪比(Signal-Noise Ratio, SNR=-7 dB)。

Tm)+N(t)

(27)

Tm=mTf+T0m=0,1,…,M-1

(28)

式中：Tm为第m个故障冲击发生的时刻。

令采样频率fs=1 000 Hz，仿真信号长度L=2 000，周期性冲击信号与含噪声周期性冲击信号如图3所示。采用所提出的自适应TQWT滤波器特征提取算法分析含噪信号，自适应可调品质因子小波构造的结果如图4所示。其中品质因子与冗余度初始值QL与rL均为2，搜索步长τQ与τr均为0.1，边界值QU与rU分别为6与5，中心频率比合理阈值T为0.05。根据能量加权归一化小波熵优化品质因子与冗余度的结果可知，品质因子Qopt=3能稀疏地表达周期性故障冲击特征，并考虑冗余度对计算成本的影响，折中选择ropt为3.5。结合阈值T，确定的合理分解层数Ja为19。

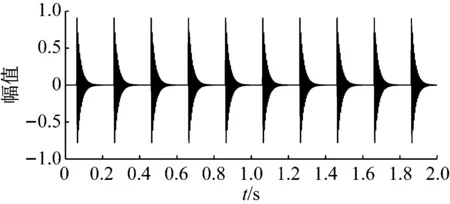
(a) 周期性冲击信号

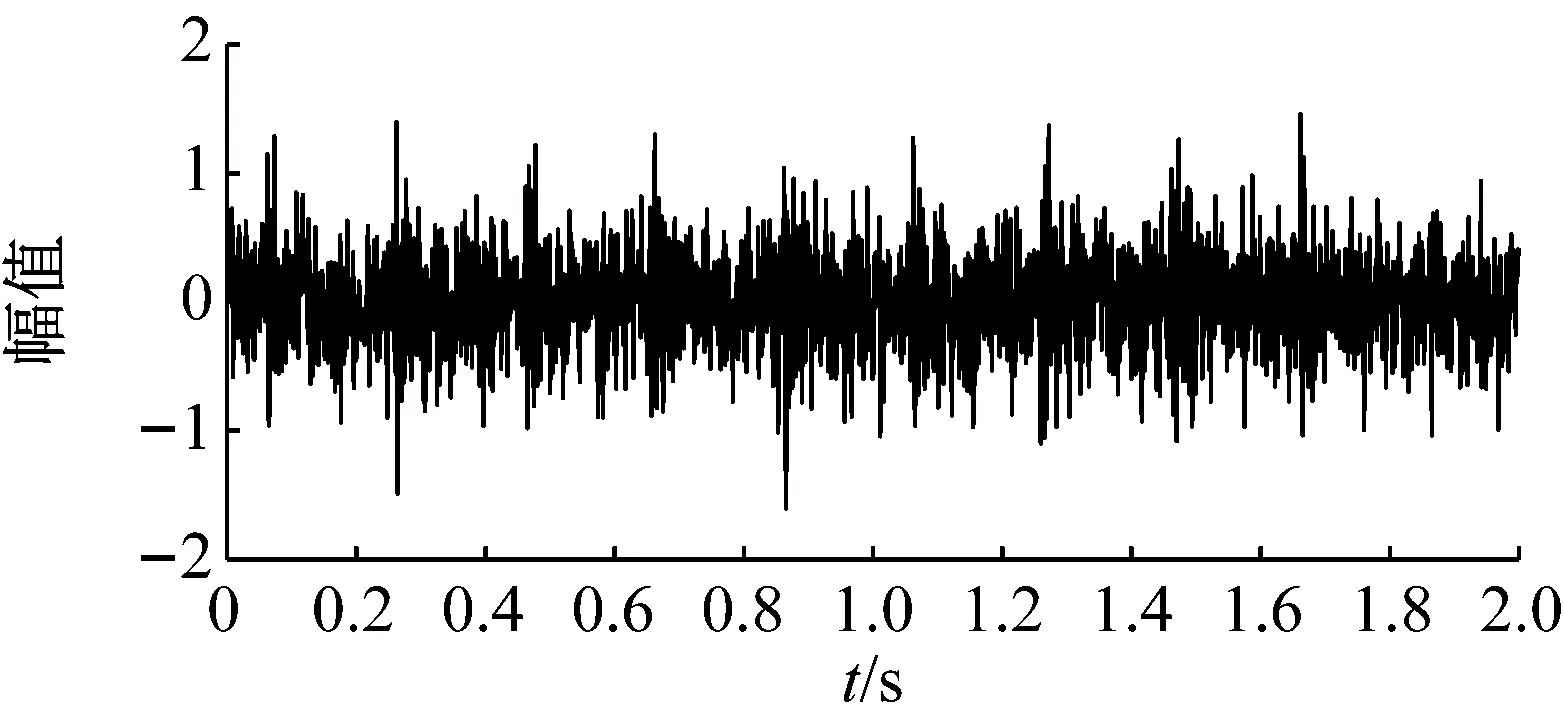
(b) 含噪声周期性冲击信号

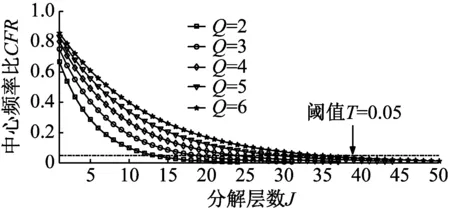
(a) 基于中心频率比的合理分解层数选择结果(r=3.5)

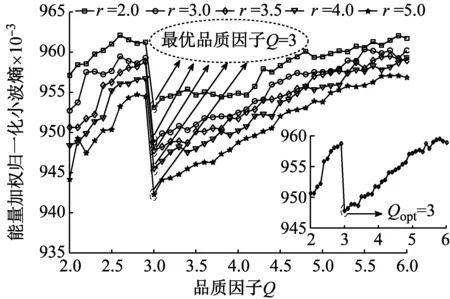
(b) 能量加权归一化小波熵优化品质因子与冗余度结果

利用最优TQWT参数组合(Qopt,ropt,Ja)分解含噪模拟信号，以冲击特征指标引导最优特征子带的选择，结果如图5所示。最大冲击特征指标对应的子带5为最优特征子带jopt。经最优特征子带的单支重构，降噪信号所提取的冲击特征及包络谱见图6。图6(a)中，周期为0.2 s的冲击特征十分显著；此外在图6(b)中可辨识出冲击故障特征频率ffault(5 Hz)的1倍频～5倍频成分，占明显主导优势。可见，自适应TQWT滤波器算法能够自适应地选择TQWT参数，并确定最优特征子带进行信号重构，实现强噪声干扰下微弱冲击特征的提取。

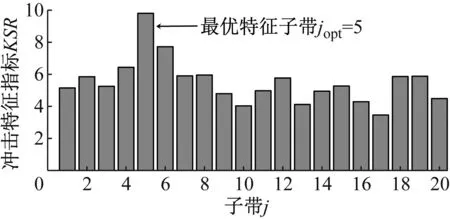
图5 最优特征子带选择结果

(a) 提取特征时域波形图

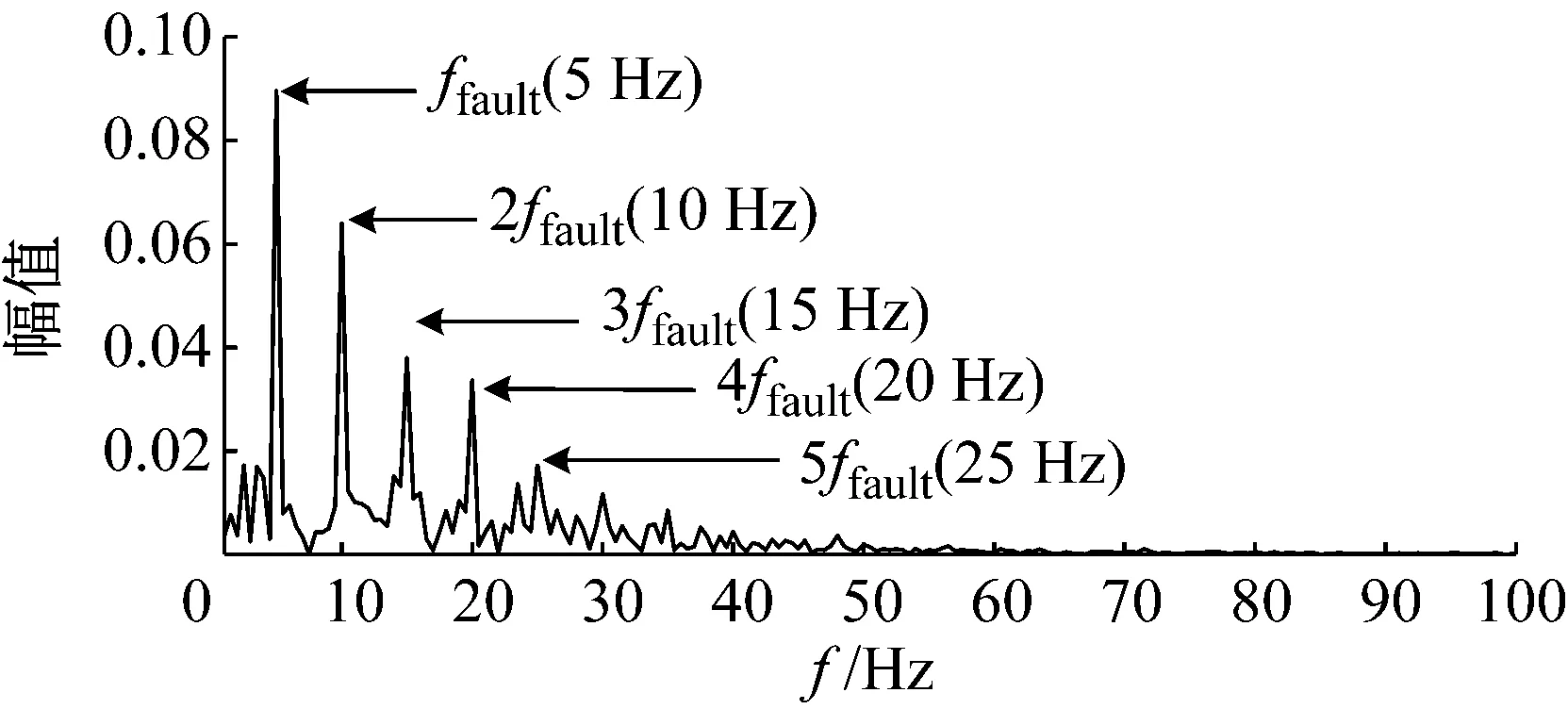
(b) 提取特征Hilbert包络谱

作为对比，利用快速谱峭度[18]与DB8小波降噪方法对仿真信号进行分析，结果如图7与图8所示。图7(b)为谱峭度滤波(最优尺度为2.6，中心频率为208 Hz)信号的包络谱，可观测到故障特征频率及倍频(ffault～4ffault)，但故障特征频率幅值相比图6(b)较小，且仍存在明显的噪声干扰频率成分。类似地，由图8可知，DB8小波降噪方法虽取得一定的消噪效果，但仍存在部分噪声干扰成分，消噪效果与周期性冲击的明显程度不如本文所提方法。

为进一步定量评估上述三种方法的特征提取效果，选取消噪后信号的峭度，SNR，均方根误差(Root Mean Squared Error, RMSE)以及包络谱的故障特征比(Failure Characteristic Rutio, FCR)为定量指标。其中，故障特征比FCR衡量消噪信号包络谱中故障特征频率及高阶倍频的突出程度，定义为

(29)

式中：ffault与ES(·)分别为故障特征频率与消噪信号的包络谱幅值。根据表1所示三种方法特征提取的定量指标对比结果可知，本文所提方法冲击特征提取结果的峭度值最大，SNR最高，RMSE最小，FCR最高，因而特征提取效果相比最佳。

(a) 仿真信号快速谱峭度图

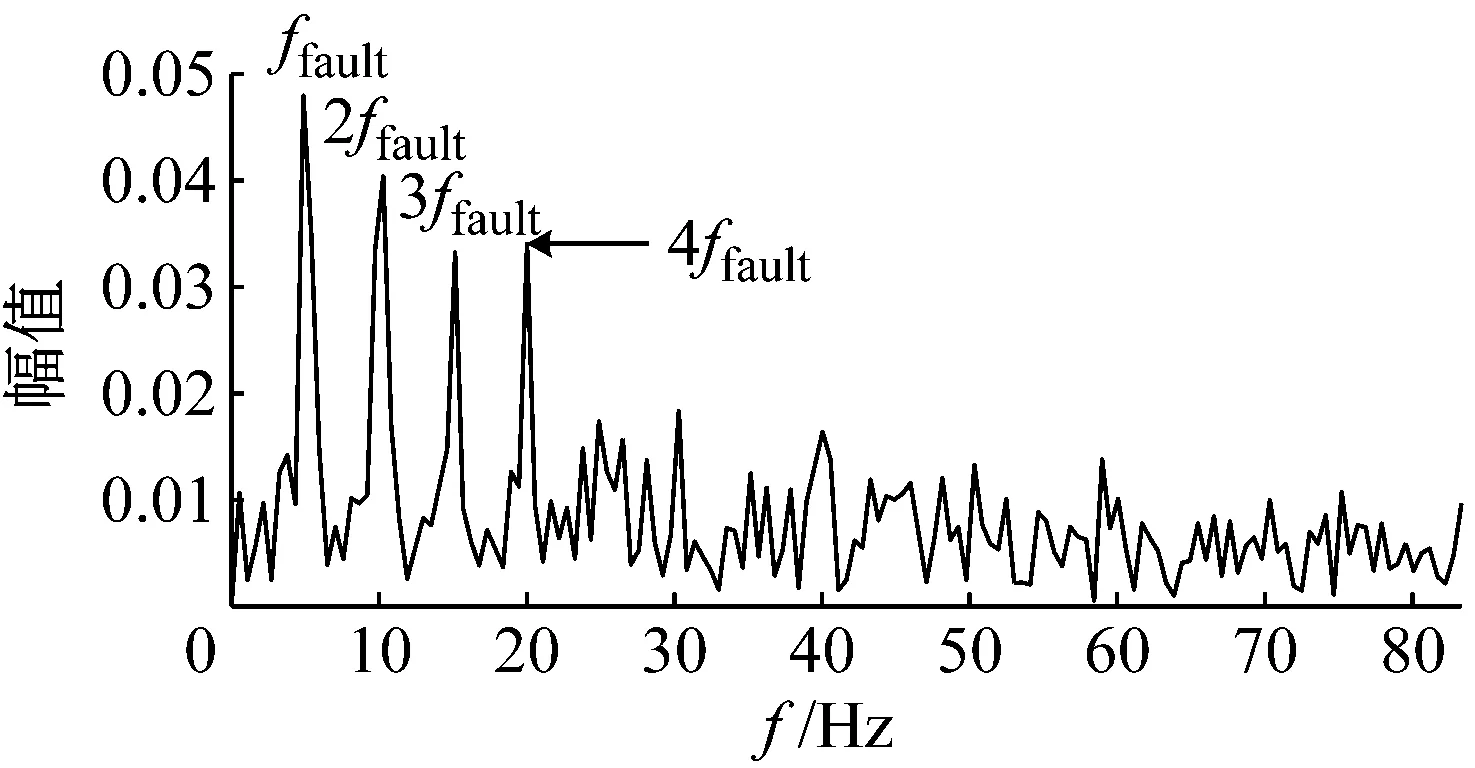
(b) 谱峭度滤波信号Hilbert包络谱

图8 DB8小波降噪对仿真信号特征提取结果

Tab.1 Quantitive index comparison of different methods for feature extraction of the simulated signal

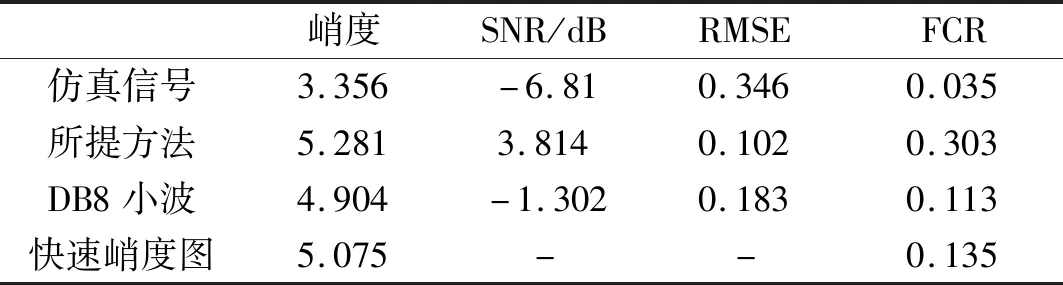
峭度SNR/dBRMSEFCR仿真信号3.356-6.810.3460.035所提方法5.2813.8140.1020.303DB8小波4.904-1.3020.1830.113快速峭度图5.075--0.135

4 试验验证

为进一步验证算法有效性，将所提出算法用于美国SpectraQuest公司机械故障仿真器采集的轴承故障振动数据。试验过程中，为模拟实际工况下谐波成分及强背景噪声对微弱故障冲击的干扰，安装附加有不平衡质量圆盘转子，并移除加速度传感器(ICP 623C01型)与NI数据采集系统之间的PCB信号调理器。试验轴承选用ER16K型深沟球轴承，利用线切割方法预制轴承外圈故障，轴承主要规格参数如表2所示。

测试过程中，采样频率设置为20 kHz，电机轴的转速大致稳定在1 440 r/min(转频fr=24 Hz)，相应轴承外圈局部损伤的故障特征频率fo为85.74 Hz。由图9(a)给出的原始振动信号时域波形可知，信号波形杂乱含有大量谐波干扰以及噪声成分并且受到强直流偏置成分的干扰，冲击成分周期性不明显。图9(b)和(c)分别为去除直流成分的时域波形及包络谱分析结果，Hilbert包络谱虽然能够识别出故障特征频率及其低次倍频，但电源工频与转频组合带来的干扰频率fpower-fr占据主导地位，进而影响轴承故障的识别。

表2 试验轴承规格参数

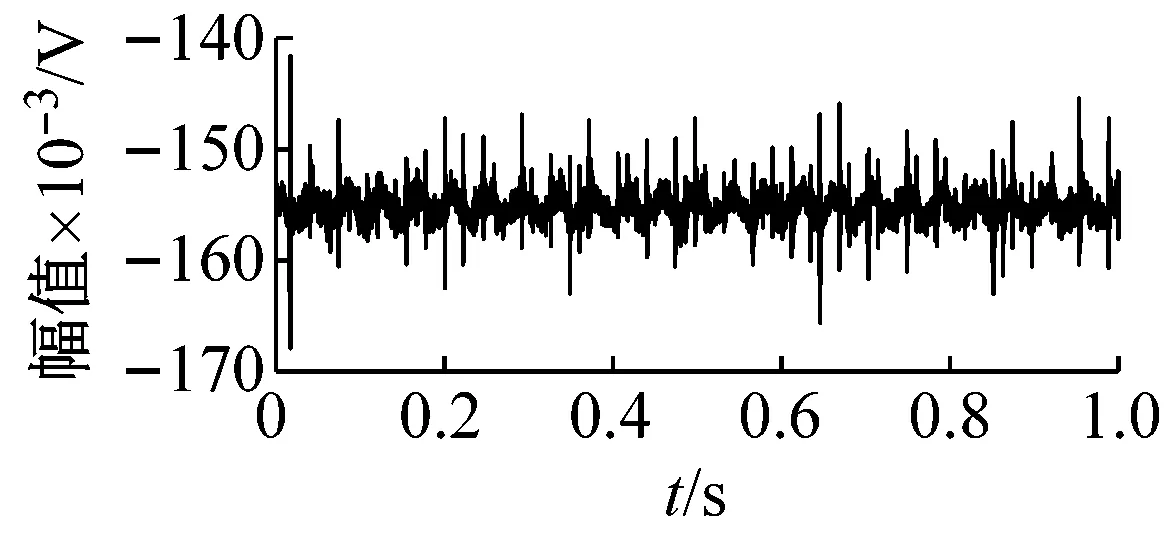
(a) 原始振动信号时域波形

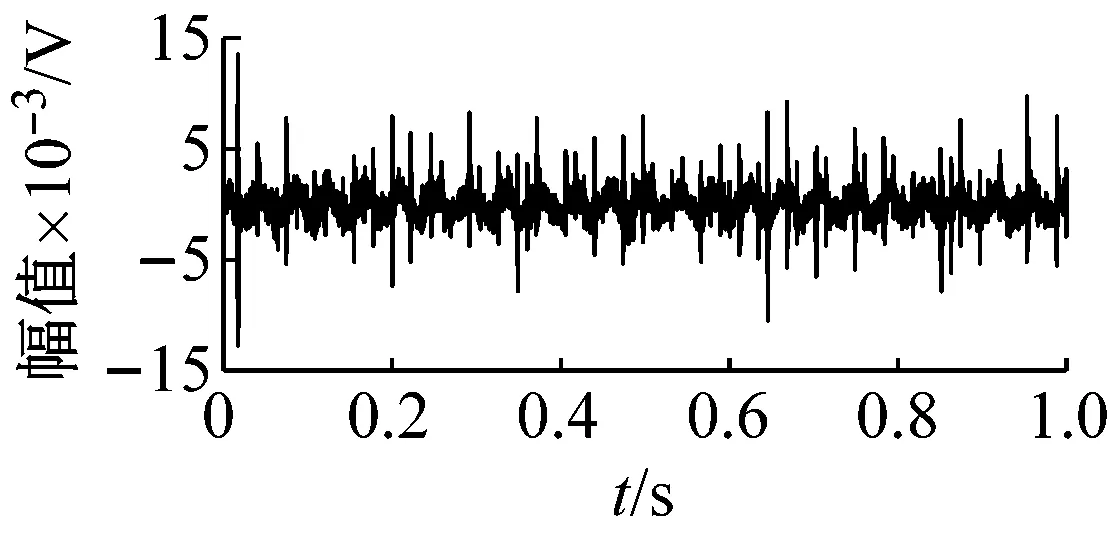
(b) 去除直流成分的振动信号时域波形

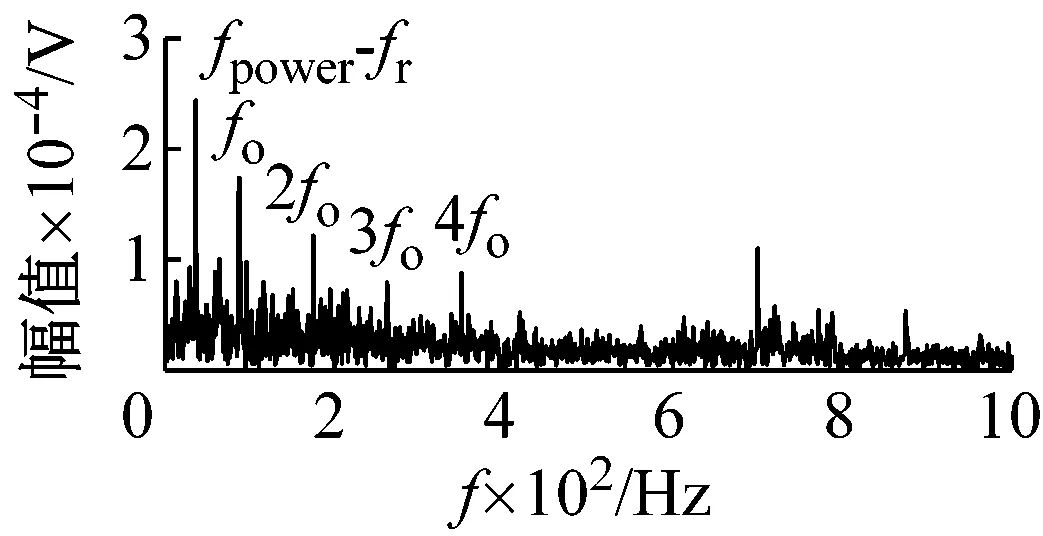
(c) Hilbert包络谱

图9 试验轴承振动信号时域波形及包络谱

Fig.9 The time waveform and envelope spectrum of the experimental bearing vibration signal

采用本文所提出方法对去除直流成分的振动数据进行分析，自适应可调品质因子小波构造的结果见图10(a)，其中品质因子与冗余度初始值QL与rL均为2，搜索步长τQ与τr分别为0.1与1，边界值QU与rU均为8，中心频率比合理阈值T为0.04。发现品质因子Qopt=3以及冗余度ropt=8对应的可调品质因子小波能够最稀疏地表达周期性故障冲击特征，此时结合阈值T所确定的合理分解层数Ja为47。进一步利用冲击特征指标引导最优特征子带的选择，确定冲击特征指标最大的子带1为最优特征子带jopt，结果见图10(b)。

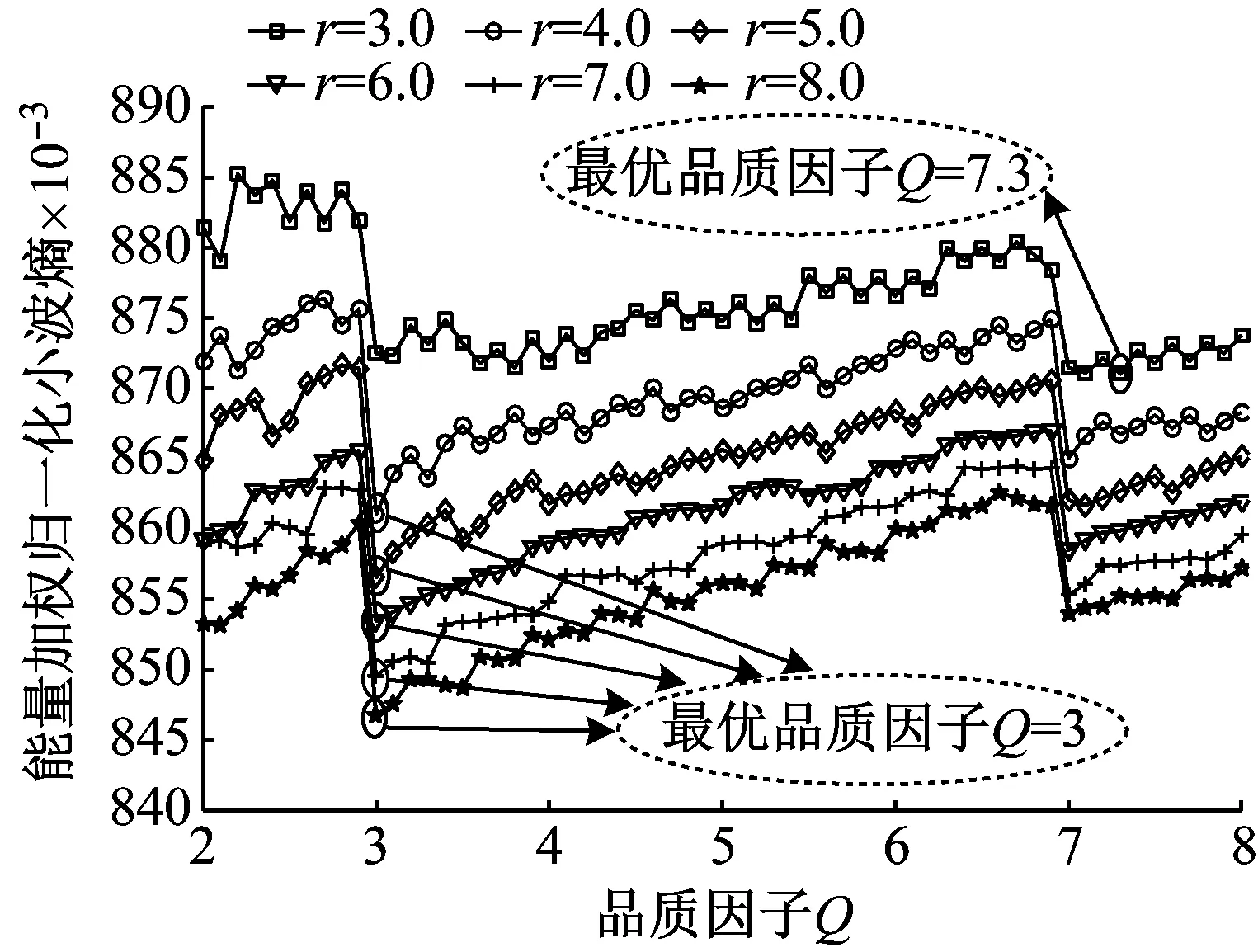
(a) 能量加权归一化小波熵优化品质因子与冗余度结果

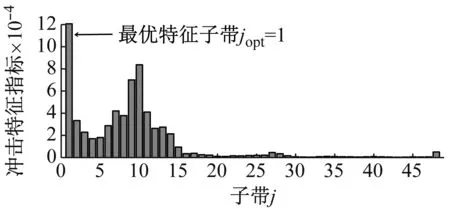
(b) 最优特征子带选择结果

Fig.10 The results of parameter selection for adaptive TQWT filter applied to the experimental bearing signal

最后利用TQWT逆变换对最优特征子带进行单支重构，重构信号所提取的冲击特征及包络谱如图11所示。对比图9(b)可知，图11(a)所示的降噪信号较好地消除了谐波以及噪声成分干扰，周期性冲击特征十分显著。图11(b)所示提取特征的包络谱，不仅避免了电源工频以及偏心转子系统转频所带来的干扰频率成分，而且还清晰地揭示了故障特征频率及其高阶倍频，从而更精确地诊断了多源干扰下的轴承故障。

(a) 提取特征时域波形图

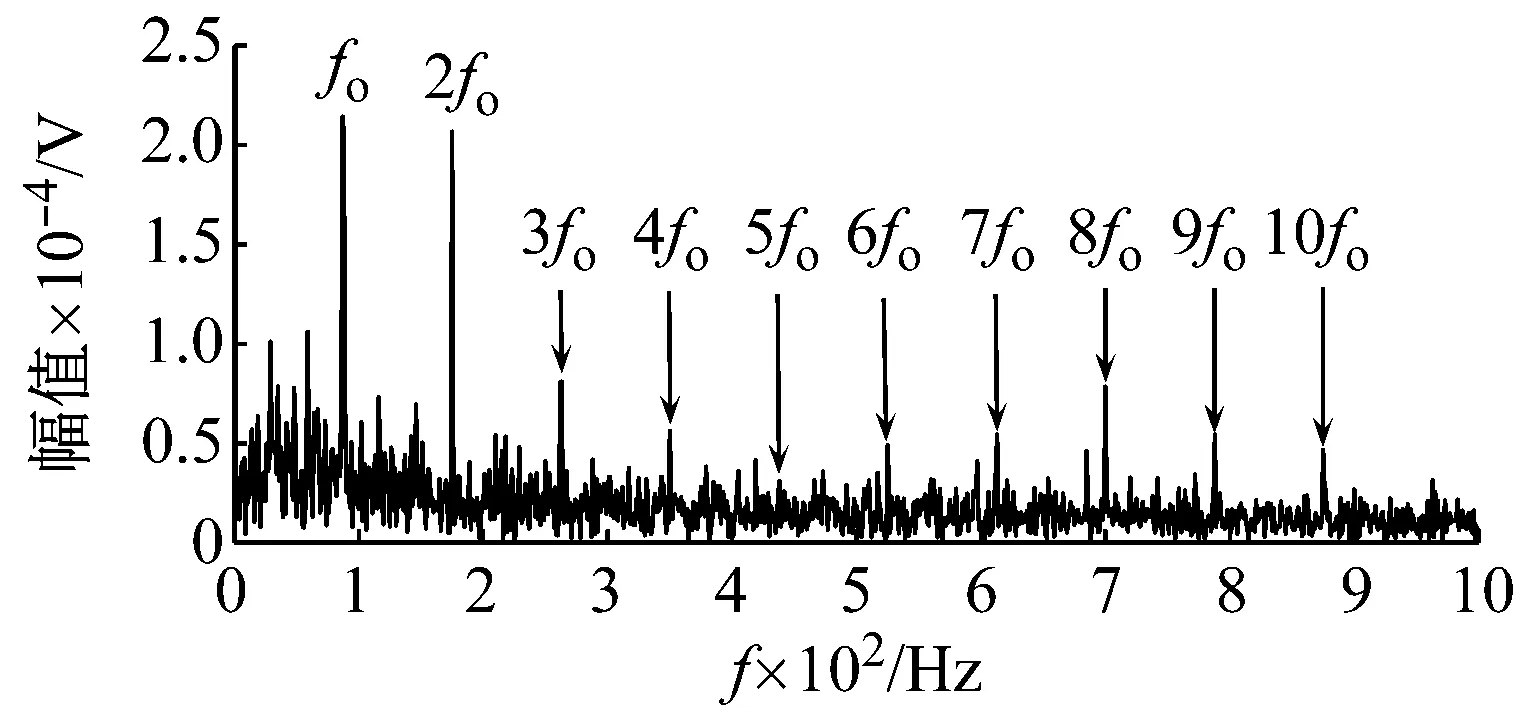
(b) 提取特征Hilbert包络谱

Fig.11 The feature extraction results of the adaptive TQWT filter applied to the experimental bearing signal

进一步利用快速谱峭度法进行对比分析，结果如图12所示。图12(b)所示谱峭度滤波(最优尺度为1，中心频率为7 500 Hz)信号的包络谱，可观测到故障特征频率及低阶倍频(fo～3fo)，但故障特征频率的幅值相比本文所提方法结果图11(b)较小。本文所提特征提取方法还能识别更高阶的故障特征频率倍频成分，效果更佳。

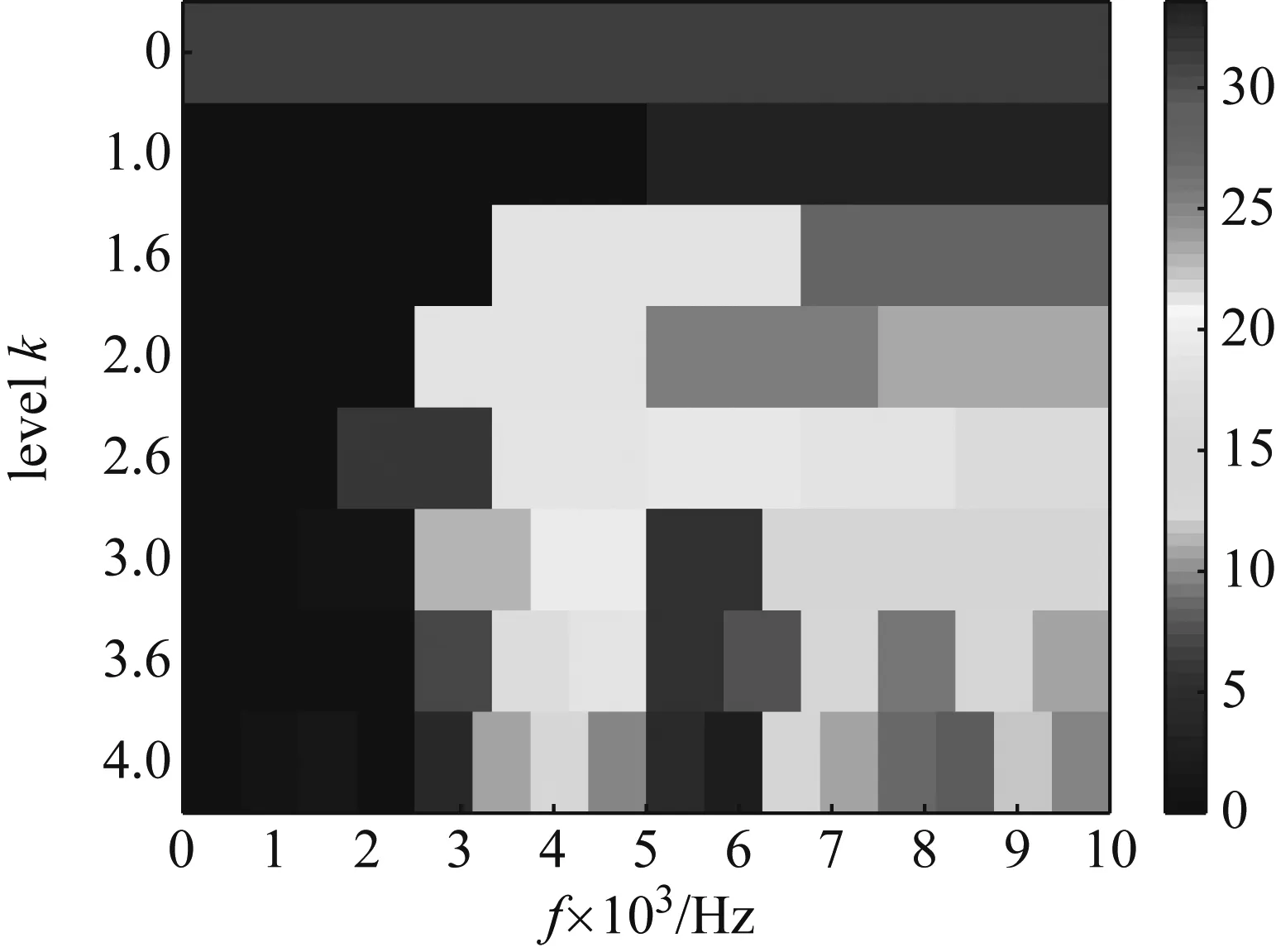
(a) 振动信号快速谱峭度图

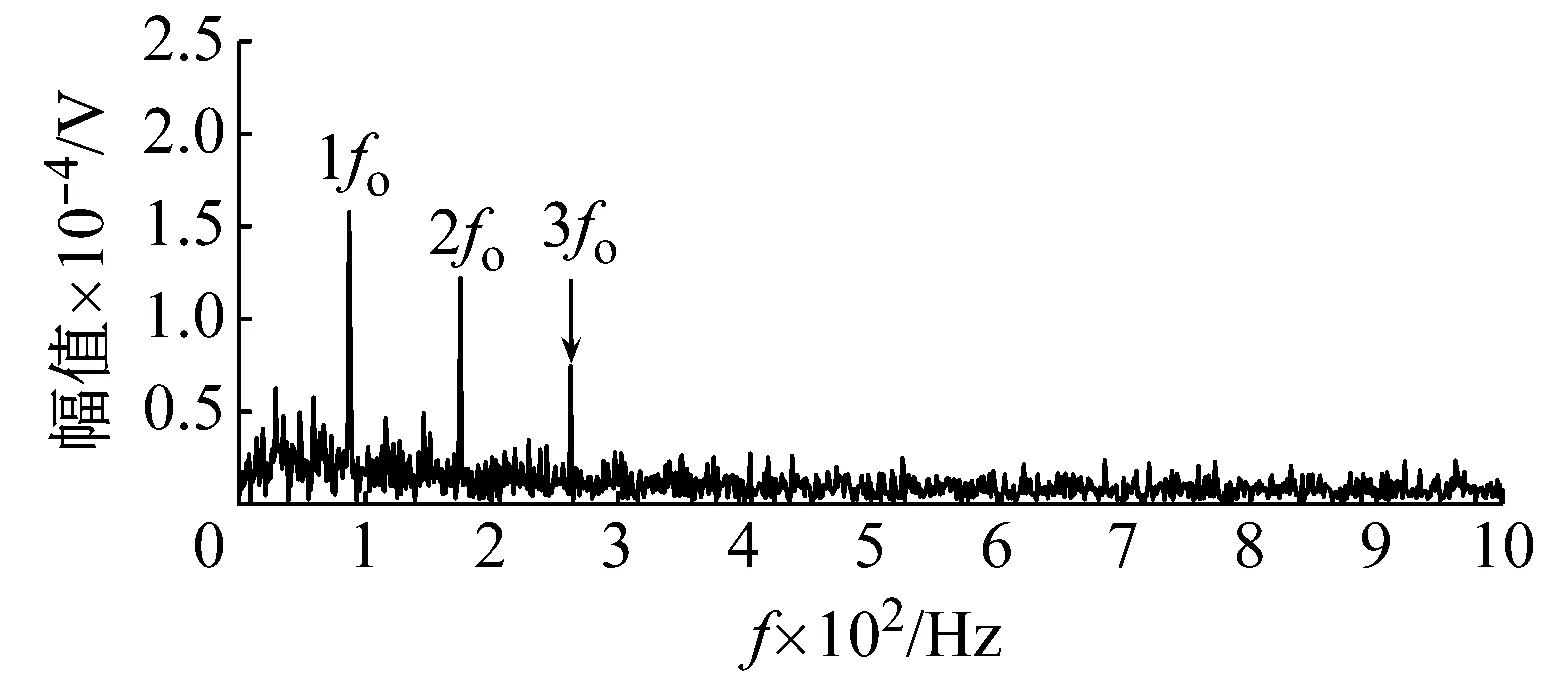
(b) 谱峭度滤波信号Hilbert包络谱

Fig.12 The feature extraction results of the fast kurtogram applied to the experimental bearing signal

4 结 论

(1) 本文提出了基于自适应TQWT滤波器的冲击特征提取算法，通过对TQWT关键参数的调控遍历搜索具有不同振荡行为的可调品质因子小波，并利用所提出的能量加权归一化小波熵评价小波基函数对故障特征信息表达的稀疏性程度，从非单一固定的小波基函数库中优化筛选出适合故障冲击特征成分表征的最佳可调品质因子小波。

(2) 本文提出了在小波变换域上，利用冲击特征指标识别含故障冲击特征信息子带的最优特征子带选择准则，能够有效定位故障特征信息子带，为后续信号的重构与降噪以及冲击特征提取提供保障。

(3) 仿真试验和实测轴承振动数据的分析表明，自适应TQWT滤波器算法能够自适应地选择TQWT参数，并确定最优特征子带进行信号单支重构与降噪，实现背景噪声干扰下的微弱冲击特征提取，并具有一定抗谐波干扰能力。