基于球颗粒DDA法的巷道围岩破坏特征分析应用初探

赵 强，王 龙，焦玉勇，黄刚海

(1.中国科学院武汉岩土力学研究所，湖北 武汉 430071；2.中国科学院大学，北京 100049；3.国家电网山东省电力公司经济技术研究院，山东 济南 250021；4.中国地质大学(武汉)工程学院，湖北 武汉 430074；5.湖南科技大学土木工程学院，湖南 湘潭 411201)

我国对能源需求巨大，而煤炭一直占主导地位[1-2]。在煤炭加速开采过程中，煤与瓦斯突出、岩爆、涌水等灾害层出不穷，而巷道冒顶是最为常见的灾害之一。巷道作为井下主要交通运输路线，其重要性不言而喻。目前用于巷道设计计算的软件多为基于有限差分法的FLAC2D/3D[3]、基于有限元理论[4-5]的ANSYS、ABAQUS以及离散元[6]UDEC/3DEC，很少使用DDA计算巷道稳定性。非连续变形分析(discontinous deformation analysis，DDA)法由石根华[7]1988年首次提出，该方法是基于岩体介质的非连续性发展起来的一种离散单元法，用于求解块体系统的大变形和大位移问题。与离散单元(discrete element method，DEM)法类似，DDA的研究对象也是由节理切割而成的块体系统，各个块体的运动用广义牛顿运动方程来描述，而块体之间保证无张力无嵌入。但不同的是DDA用最小势能原理把每个块体的变形、运动和块体之间的接触统一到联立方程组中，通过隐式积分法求解得到每个块体的位移和变形分量，再利用独创的开闭迭代准则来判断求解后未知量的准确性[8]。

目前，DDA方法已经在岩土工程相关领域得到了广泛应用。如邬爱清等[9-10]利用二维非连续变形分析(DDA)法模拟得出千将坪滑坡启动的识别方法以及清江水布垭地下厂房在复杂地质条件下变形特征；吴建宏等[11]利用三维块体DDA模拟预测了岩体边坡失稳过程；甯尤军等[12]利用非连续变形分析(DDA)法模拟再现了岩石爆破过程中的炮孔扩张、岩体破坏、块体抛掷和爆堆形成过程；张开等[13]采用不连续变形分析(DDA)软件对影响巷道开挖变形的岩体力学因素以及围岩变形规律进行数值模拟分析；刘永茜等[14]运用改进的非连续变形分析方法(DDA)模拟了鹤壁煤电股份有限公司十煤矿煤巷掘进时一次煤与瓦斯突出过程；王文等[15]基于改进的SSOR-PCG方法分析了某节理岩体巷道围岩的破坏过程；左建平等[16]在室内相似模拟结果的基础上，采用非连续变形DDA方法对深部采用影响下的断层活动规律进行了探讨；靖洪文等[17]采用DDA方法定量研究了非连续围岩体位移影响因素的变化规律；杨建立等[18]基于不连续变形数值分析方法模拟分析了多条断层对工作面综放开采的影响规律；鞠杨等[19]应用DDA数值方法模拟分析了深部煤矿开采中上覆岩层的应力场变化和变形移动规律。

现有研究成果主要集中于块体DDA方法的研究和应用，然而块体DDA法具有接触问题复杂、计算效率低等局限性。相比之下，球颗粒DDA将原DDA块体单元简化为球单元，接触问题大大简化，在一定程度上提高了计算效率和求解问题规模。本文基于球颗粒DDA法计算原理，以贵州小屯煤矿运输巷道为研究对象，以巷道围岩变形的现场实际测量结果为基础，对巷道围岩的变形破坏特征进行了模拟和对比分析，进一步探讨了球颗粒DDA法在巷道围岩变形破坏过程中的应用。

1 球颗粒DDA方法基本原理

1.1 球颗粒接触模型

传统DDA为块体单元，二维块体接触模式为角-角接触、脚-边接触和边-边接触，而三维块体与块体之间接触形式更为复杂，编写程序也存在很大困难，且开闭迭代接触判断准则计算耗时较大。因此为简化三维接触问题，将原DDA块体单元简化为刚性球颗粒，仅使用球心坐标和半径就可表示球体在空间中的位置，球颗粒之间是否接触可用两球心距离与半径之和相比来判断。简化后的球颗粒DDA接触模式主要有球-球接触、球-面接触、球-边接触三种(图1)，其中固定面可作为边界固定条件。

图1 球颗粒接触模型Fig.1 Contact model in SDDA

1.2 球颗粒位移

球颗粒DDA将球体简化为刚体，不考虑其自身变形，基本未知量可假设为式(1)。

(1)

式中：(dxdydz)指球心的刚体平动未知量；(rxryrz)指球体绕球心的转动未知量。

当球颗粒只做平动运动时，球体上任意一点的位移见式(2)。

(2)

当球颗粒只做自转运动时，球体上任意一点的位移见式(3)。

(3)

把式(2)和式(3)相加，可得一般情况下刚体球颗粒任意一点的总位移矩阵，见式(4)。

(4)

其中

为形函数矩阵。

1.3 建立总体平衡方程组及其求解

假设模型系统有n个球颗粒单元，可建立总体平衡方程[20]，见式(5)。

(5)

式中：[Kij](i,j=1,2,…,n)是6×6的刚度子矩阵，[Kii]仅与球颗粒i的属性有关，[Kij] (i≠j)与球颗粒i和j的相互作用有关；[Di]是6×1的球颗粒i的基本未知量子列阵，[Fi]是6×1的球颗粒i的广义力子阵列。

在球颗粒系统中，所有接触力子矩阵和位移变量都来自与它相邻的球颗粒之间的相互作用。根据最小势能原理，对相关量求偏导，所有外力和内力都转换为对应的子矩阵，最后再加到总体平衡方程的相应位置上。至此，采用直接法或者迭代法隐式求解总体平衡方程的未知量，更新球颗粒位置。

2 球颗粒DDA计算模型的建立

2.1 工程概况

贵州大方煤业小屯煤矿位于扬子板块川滇黔盆地、黔北断拱内，井田属于构造剥蚀山地地貌为主的低、中山地区，大部分标高在+1 350 m以上。大方县位于贵州西北部，降雨丰富，地下水储量大。受此影响，小屯煤矿矿井涌水量较大，大量地下水经三条平硐排除。由于排水沟防渗性不好，以及北翼采空区积水等其他水源的渗入，平硐部分地段地下水积聚，排水沟冲毁，影响矿井的正常生产。

自第四中部车场至后段，平硐逐渐穿过倾斜的各可采煤层，巷道围岩转为以泥灰岩和粉砂质泥岩为主，并含有大量的蒙脱石、伊利石等膨胀类黏土成分。经矿物成分分析黏土含量达50%以上，围岩本身强度低，具有很强的遇水膨胀性和崩解性，对巷道围岩的稳定性十分不利。在部分地段产生严重底鼓、围岩开裂和顶板下沉等状况，地下水与含有大量黏土矿物的泥岩反应，巷道出现了两帮收缩严重、顶板开裂冒落、底鼓剧烈、排水沟损毁等现象。典型的现场顶板变形现象如图2所示。

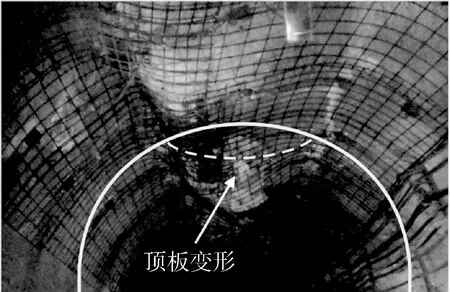
图2 巷道顶板变形现场照片Fig.2 Field photo of roadway roof deformation

2.2 数值建模

在详细分析小屯矿区地质、构造特征和调研围岩变形情况的基础上，本文选取了副平硐的第十中部车场附近地段作为模拟对象。该地段围岩以泥灰岩和粉砂质泥岩为主，地质条件较差、顶板破碎，围岩变形严重、失稳可能性较大，因而具有代表性。巷道的地理位置及其断面尺寸如图3和图4所示。

根据小屯煤矿的地质条件，建立简化的球颗粒DDA模型如图5所示。模型大小取16 m×6 m×7 m，包含10 660个单元，其上覆岩层厚约400 m。巷道跨度5.3 m，墙高1.8 m，圆拱半径2.65 m，其上覆模型厚度4.28 m。模型底部及四周边界采用固定面约束，上边界有均布荷载10 MPa。

计算模型简化为均质材料，球颗粒密度取2 500 kg/m3。模型采用的力学参数：抗拉强度取31 MPa，黏聚力取4.3 MPa，内摩擦角取43°。模型计算参数见表1。

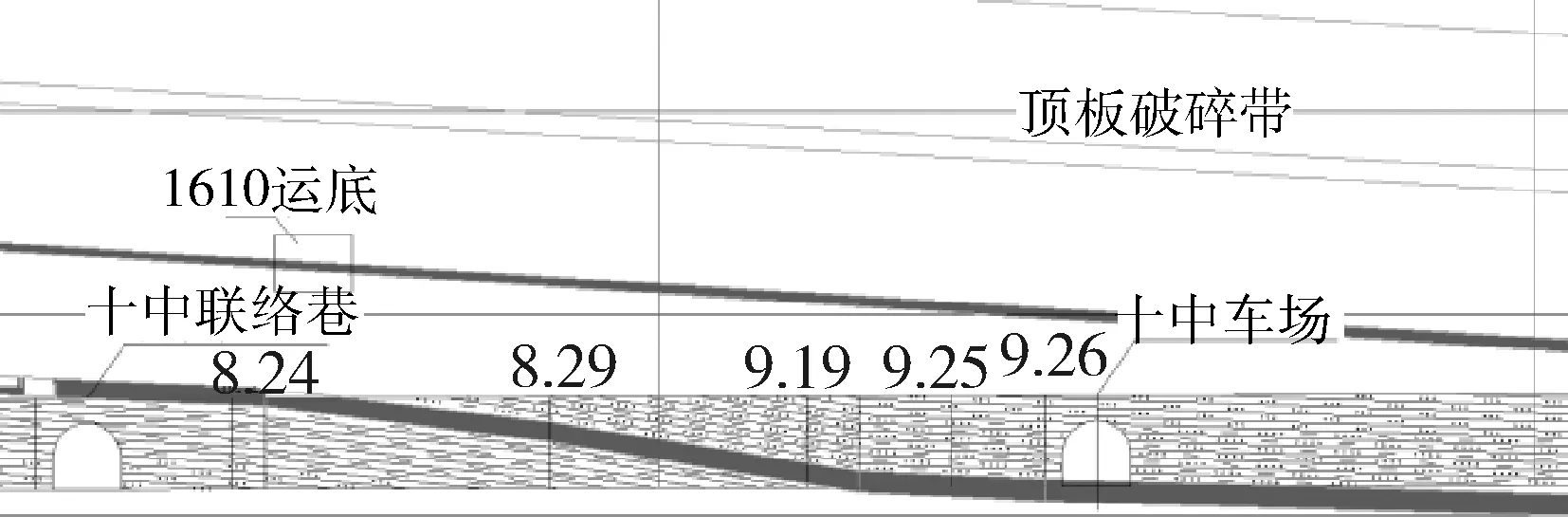
图3 数值建模巷道位置Fig.3 Numerical modeling of roadway location

图4 巷道断面尺寸Fig.4 Size of roadway section

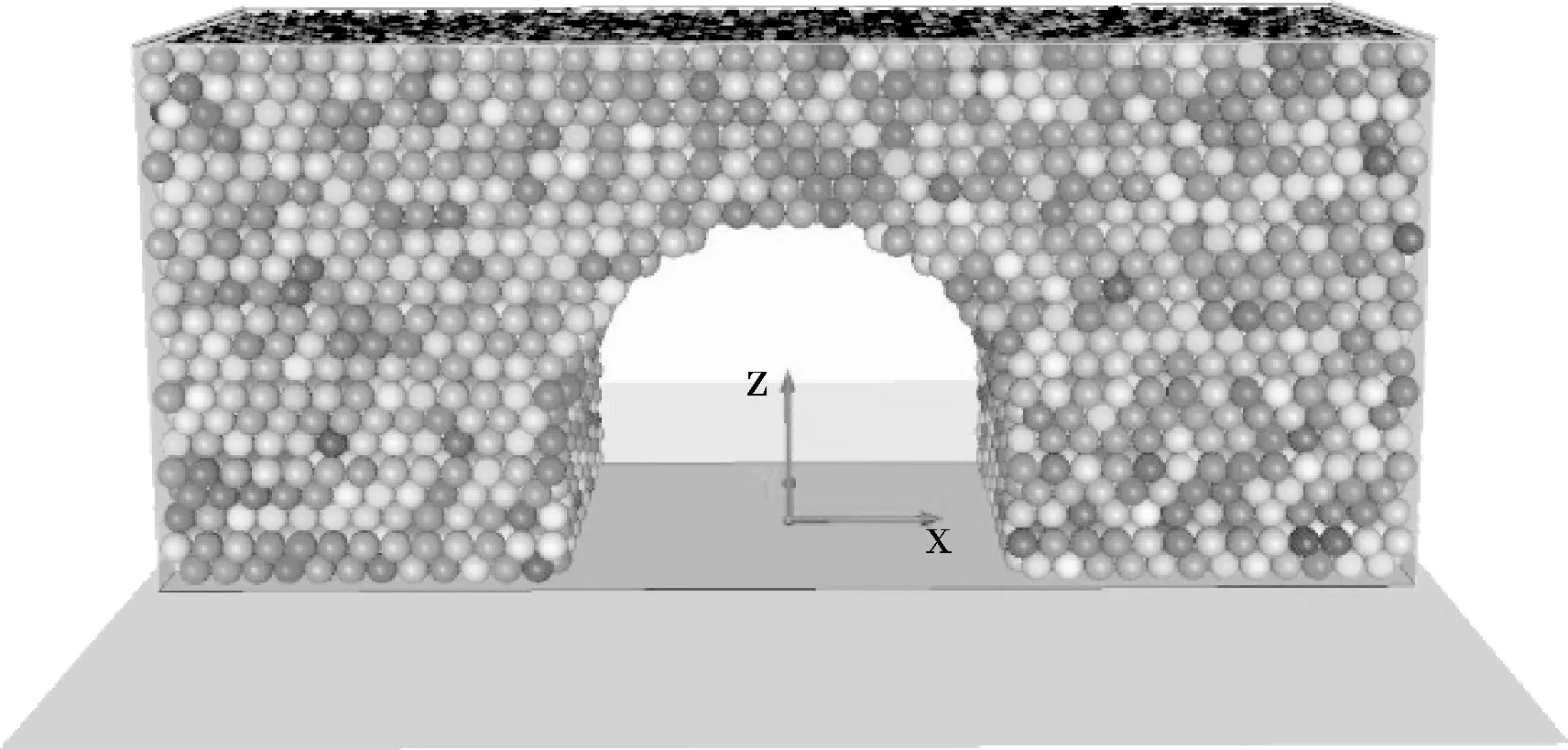
图5 数值计算模型Fig.5 Model of numerical calculation

图6 球颗粒DDA计算结果Fig.6 Calculation results of SDDA

3 结果分析

不同时步下球颗粒DDA计算得到的巷道垮塌破坏结果如图6所示。由图6可知,随着计算时步的增大，在上覆均布荷载的作用下，巷道顶部逐渐产生裂纹，进而扩展，弯曲下沉量逐渐增大，在时步为49 980时，巷道顶部裂纹贯通，下沉量巨大，破坏严重。另外，由图7也可看出，顶板随着计算时步的增加下沉量逐渐加大，最终下沉量为490 mm，与现场实际下沉情况接近。这一模拟结果与实际情况基本相符。

表1 计算参数Table 1 Calculation parameters

图7 不同时步下顶板下沉量Fig.7 Subsidence of roof with different time steps

4 结 语

相比采用有限单元法模拟巷道垮塌，球颗粒DDA方法可以很好地模拟出巷道顶部裂隙产生、扩展直至破裂的全过程。本文采用球颗粒DDA方法对小屯煤矿巷道进行了模拟，得到了巷道顶部裂隙产生、扩展、贯通直至弯曲下沉巨大、破坏的一系列情况变化，计算结果与实际结果基本相符，成功地再现了巷道顶部裂隙带产生的全过程。这充分地说明了用球颗粒DDA在模拟研究井下巷道破坏规律方面具有一定的应用前景。但是，对于巷道材料参数与球颗粒DDA计算模型参数取值之间的联系需做进一步研究确定。