基于粒子群算法的提升机主轴装置应变测点优化研究

包从望，肖钦兰，江 伟，刘永志

(六盘水师范学院，贵州 六盘水 553000)

0 引 言

多绳摩擦提升机的主轴装置作为动力及承载的关键部件，其动态特性与提升机的健康状态息息相关[1]。主轴装置不仅承载着电机的全部转矩，而且还承受钢丝绳产生的压力以及各种动载荷和冲击载荷[2]。当主轴出现弯曲、关联组件松动、旋转不平衡、轴承缺陷等故障时，通过提取主轴的振动特性以实现健康诊断，因振动特性存在数据局限性问题，会导致故障诊断的误判，且难以真实反应提升机的动态载荷。主轴装置作为核心承载部件，通过研究其应力应变信号，可定性跟踪摩擦提升机的动态载荷。目前，国内外学者针对主轴装置应力应变有较多的研究成果。游俊红[3]、WANG等[4]利用有限元分析软件，对摩擦轮的挠度变化、变形规律、应力集中实现模拟分析，并找到最大应力值点；LI等[5]对铸造式摩擦轮实现了有限元分析，重点分析了摩擦轮轮辐处的应力分布；WONLNY等[6]通过数值模拟分析，研究了摩擦轮辐板、筒壳等结构的应力分布，得出摩擦轮的危险应力点；李菁[7]通过应力应变数值模拟方式，分别分析了匀速提升过程、左右提升开始和左右提升终止五种工况时的应力变化，得出摩擦轮从开始受力到疲劳破损时的应力变化过程；王重秋[8]基于ZigBee无线信号传输协议，设计开发了提升机辐板应力检测装置，实现辐板应力的检测。

目前，主轴装置的应力应变主要集中于有限元分析、数值模拟和采用粘贴应变片的方式检测应力变化，其中最有效的方法是粘贴应变片，而主轴装置与应变片之间的面积相差较大，而目前的检测中并未对应变测点进行优化，导致信息冗余。为解决测点优化布置问题，基于改进粒子群算法对应变测点进行优化，以实现应变检测点的优化配置。

1 应变测点优化方案

图1 主轴装置应变测点优化方案Fig.1 Strain measuring point optimization scheme for spindle device

结合应变测点检测需求，确定测点优化方案如图1所示，主要分为初选测点选取和测点优化两步。根据摩擦提升机主轴装置的受力特性，建立主轴装置的力学模型，基于ANSYS软件作应力应变仿真分析，根据仿真结果选取应力集中点作为初选测点；由于初选测点数量较多，无法针对每一个测点进行检测，本文以MAC矩阵非对角元作为适应度值，利用改进后的粒子群算法对初选测点进行组合优化。

2 应变测点优化布置

2.1 基于有限元仿真的应变测点初选

2.1.1 主轴装置力学模型

1) 钢丝绳张力。提升机在正常运行中，钢丝绳与衬垫之间为弹性滑动，根据欧拉公式，计算钢丝绳与衬垫之间具有弹性滑动部分的张力见式(1)。

Fθ=F2eμθj(0≤θj≤αR)

(1)

式中：Fθ为包角部分钢丝绳的张力，N；θj为钢丝绳松边到拉紧边的转角，rad；μ为摩擦因数；F2为钢丝绳松边的张力，N；αR为弹性滑动部分的围包角，rad。

2) 摩擦轮力学模型。主轴装置的摩擦轮受力主要源于衬垫，根据钢丝绳的作用形式分为径向和切向力(图2)，微弧段尺寸与摩擦轮直径之比为无穷小，可将微弧段的受力看作平面共点力系，根据受力平衡方程有式(2)。

(2)

式中：F为钢丝绳单元在B点的张力，N；Δθ为Δl微弧段对应的圆心角，rad；ΔF为A点到B点的张力差，N；ΔN为摩擦轮对微弧的支撑力，N。

图2 钢丝绳单元受力分析Fig.2 Force analysis of wire rope unit

因Δl较小，故有ΔF≈0，sin(Δθ/2)=Δθ/2，式(2)可简化为式(3)。

ΔN=FΔθ

(3)

结合压强理论和式(1)，可得摩擦轮所受径向力和切向力见式(4)和式(5)。

(4)

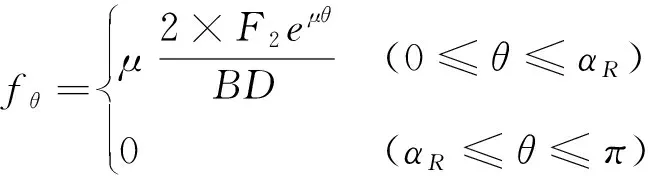
(5)

2.1.2 主轴装置有限元分析

1) 主轴装置三维建模。根据提升机生产厂商提供的提升机主轴装置参数，选择一种便于实验的主轴装置，其摩擦轮直径、围包角、最大静张力、摩擦系数分别为：0.8 m、180°、15 kN、0.25。根据主轴装置的主要参数，基于Pro-E三维建模软件，建立主轴装置三维模型。

2) 网格划分及边界条件。根据主轴装置现场运行环境，摩擦轮的材料为45 Mn，主轴为16 Mn，根据表1的材料属性，设置模型材料，采用Mechanical网格划分方式，对摩擦轮实现网格划分，节点总数为271 923，单元总数为67 275。

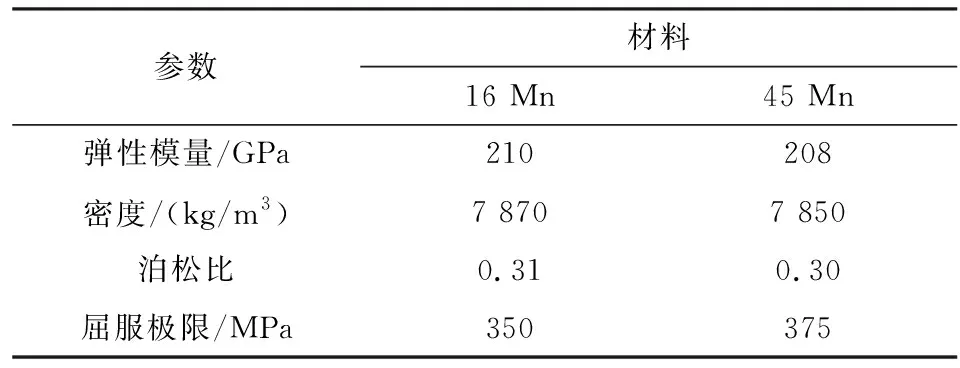
表1 主轴装置材料属性Table 1 Material properties of main shaft device

边界条件设置中，将蠕动弧度边设定为180°，以最大静张力为张紧侧拉力，则F1=15 kN，根据式(4)和式(5)可得径向力和切向力的应力分布理论计算公式见式(6)和式(7)。

(6)

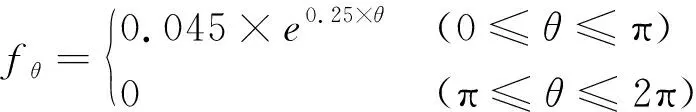
(7)

3) 主轴装置应力仿真结果。根据边界条件设定仿真结果，对主轴装置加载后进行求解，得到总变形云图和应力云图，其中最大变形值为0.4168 mm，位置靠近摩擦轮中部；最大应力值为91.41 MPa，小于45 Mn的屈服极限375 MPa。

2.1.3 应变测点初选

测点选择过程中首先考虑其可行性，由于摩擦轮外侧有压块，不易设置测点，因此选择摩擦轮内部和轮辐位置进行贴片，据此，根据应力仿真结果选择初选测点。

1) 摩擦轮内壁测点初选。根据摩擦轮内壁应力仿真结果，选取具有应力代表性的点作为初选测点，如图3所示。由于A点为轮辐与内壁的交界处，不易粘贴应变片，因此该点舍去，从左往右依次选择1～7个初选测点。

2) 摩擦轮轮辐测点初选。摩擦轮轮辐的应力路径有径向和切向两条应力路径，如图4所示，应力路径分别从点C1到点C2，点1到点2。根据应力仿真图，选择点8和点9为轮辐的初选测点。

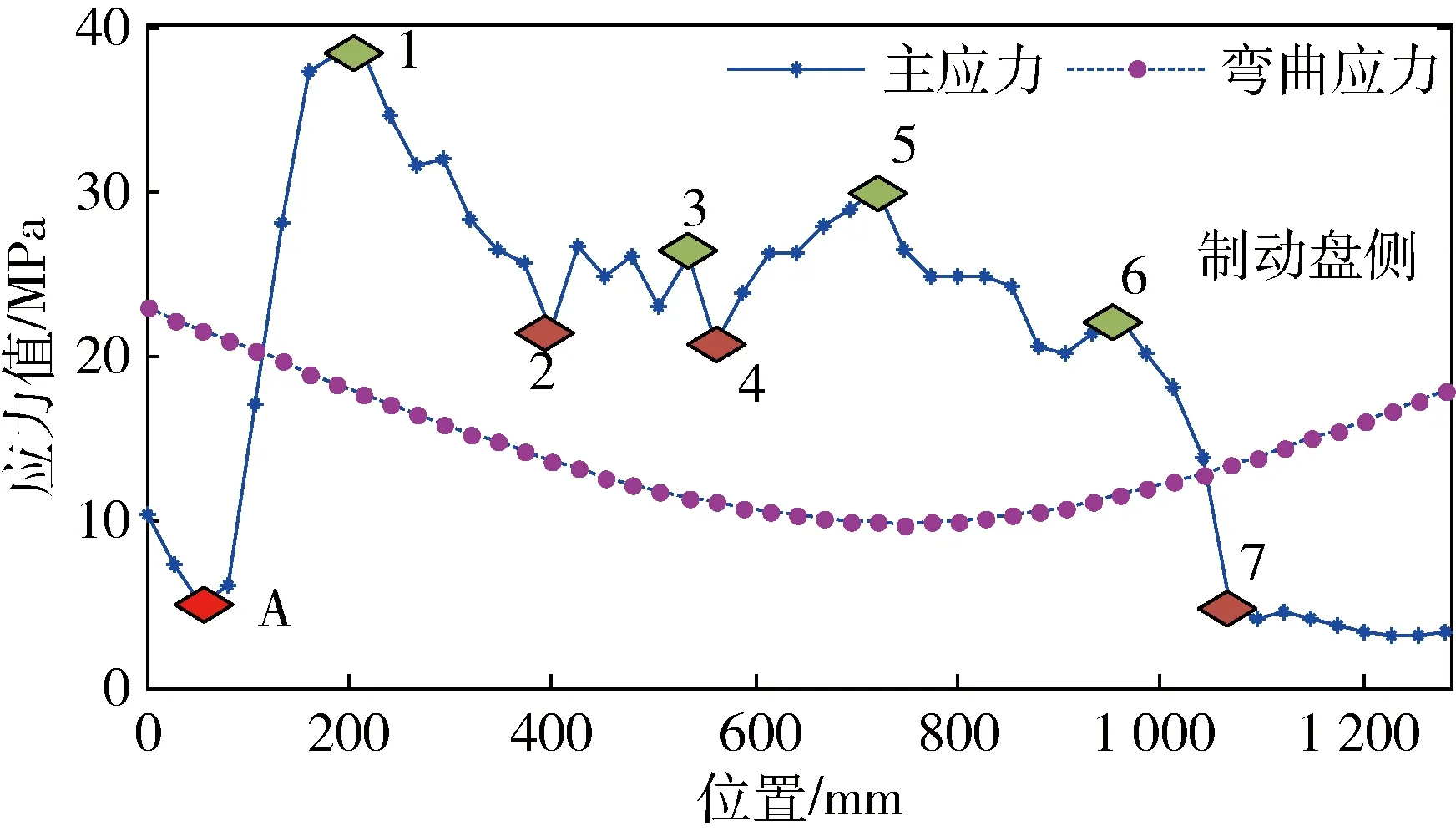
图3 摩擦轮内壁测点初选Fig.3 The primary selection of friction wheel inner wall measurement point

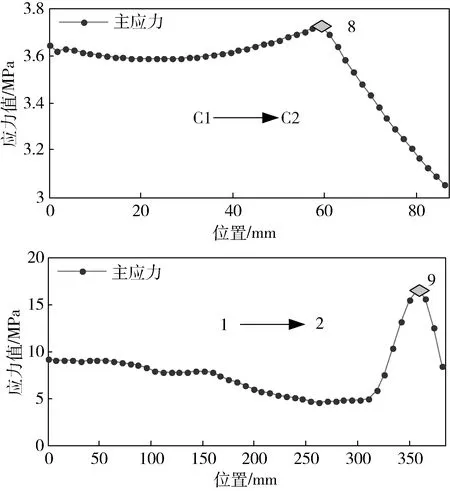
图4 摩擦轮轮辐测点选择结果Fig.4 The results of friction wheel spoke point selection

3) 主轴测点初选。主轴测点初选中，选择轨迹从离摩擦轮较近的点1到较远的点2，根据图5中的应力图，选择测点10和对称位置测点11，以便计算主轴的弯曲应力和主应力。

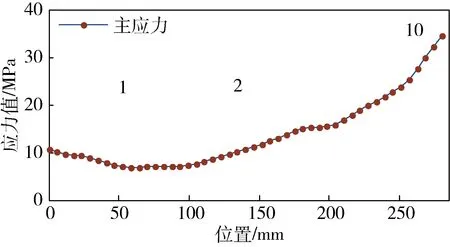
图5 主轴测点初选结果Fig.5 The results of main shaft device primary measurement point

2.2 粒子群算法的改进

1) 粒子群算法。粒子群算法寻优过程中，首先对随机群体赋予初值，由初值开始更新迭代，直至找到最优值，更新迭代过程中其粒子有三个属性，分别为：①当前值：pi=(pi1,pi2,…,pim);②个体最优位置：opi=(opi1,opi2,…,opim);③更新速度：vi=(vi1,vi2,…,vim)。

位置和速度的更新过程见式(8)和式(9)。

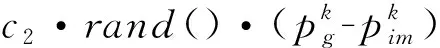
(9)

2) 改进粒子群算法。粒子群算法在寻优过程中常会遇到局部最优的问题，为使粒子跳出局部最优，对更新后的位置和速度采用交叉操作的方式，即在局部最优的位置能产生新的粒子以跳出局部最优位置，粒子群算法中引入交叉操作的过程见式(10)和式(11)。

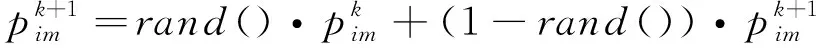
(11)

2.3 基于粒子群算法的应变测点优化

1) 粒子群算法寻优准则。由动力学理论，在主轴装置测量过程中，由于受噪声干扰，难以保证质量矩阵和刚度矩阵的正交性[10]，为解决该问题，对检测点数和检测位置可通过模态置信准则对测点数和位置进行量化。模态置信准则可体现模态振型的空间交角，见式(12)，MAC值越大，空间交角越小，反之越大。

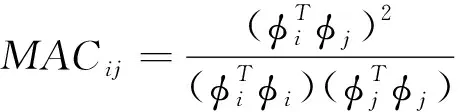
(12)

式中，φi、φj为主轴装置的第i、j阶振型模态向量。

2) 主轴装置模态仿真。根据粒子群算法的寻优准则，首先要对主轴装置进行模态分析，基于ANSYS软件对主轴装置求解模态振型，求解阶数为8阶。初选测点的网格节点及其对应位移模态(表2)。

表2 主轴装置初选测点前8阶位移模态Table 2 The first 8th order displacement mode of the primary measuring point of the main shaft device

3) 粒子群算法寻优结果。利用Matlab编程，设定粒子群规模为20，粒子范围为[1，165]，速度[-0.5，0.5]，粒子维度为8，加速度常数c1、c2为2，惯性权重取经验值0.927，测点组合数从2个开始搜索直至全部搜索完成。为验证粒子群算法的改进效果，举例测点数为8时的收敛情况，改进后的迭代次数为29次，改进前为34次，最小优化值均为0.21。

根据优化结果，统计最优组合及对应适应度值，根据经验分析，当MAC矩阵非对角元小于0.25时有较好的模态识别效果，因此选择适应度值在0.25以内的，通过测点优化结果可知当测点数小于8时均能达到该效果，当测点数为8时的组合为1，5，6，7，8，9，10，11；当测点数为7时组合为1，6，7，8，9，10，11；当测点数为6时组合为1，6，8，9，10，11；当测点数为5时组合为1，6，9，10，11；当测点数为4时组合为6，9，10，11；当测点数为3时组合为6，9，10；当测点数为2时组合为6，9。

3 实验结果与分析

为验证主轴装置应变测点优化效果的有效性，对在主轴装置安装前先在摩擦轮内部贴好应变片，为保证贴片的可靠性，在优化测点的对称位置选出候选测点。

应变检测过程中采用无线应变仪检测主轴装置的应变信号，截取8个测点部分应变信号，如图6所示，测点1、测点5、测点6、测点7、测点8、测点9、测点10、测点11分别对应1～8通道的应变信号，通过应变计算轮辐和筒壳最大主应力分别为16.8 MPa、91.8 MPa，主轴弯曲应力为52 MPa，对应扭矩为57.9 kN·m，与仿真结果接近。该结果为后续主轴装置故障诊断、载荷研究提供了依据。

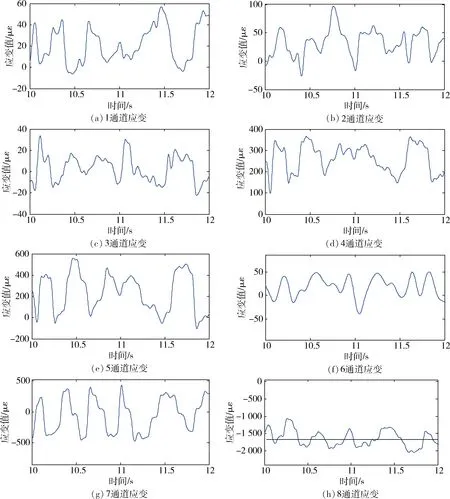
图6 测点应变检测结果Fig.6 The results of strain measurement

4 结 语

本文以模态置信准则MAC值为适应度函数，基于改进后的粒子群算法对提升机主轴装置应变测点进行了优化。首先对主轴装置进行三维建模，基于ANSYS软件对主轴装置实现应力应变仿真及8阶的模态仿真；从仿真结果中寻找出11个特殊点作为应变检测的初选测点；在模态仿真中标定初选测点对应的网格节点，并求出其8阶振型的位移模态；利用改进后的粒子群算法对初选测点进行组合优化，优化组合测点为测点1、测点5、测点6、测点7、测点8、测点9、测点10、测点11。通过验证，改进后的粒子群算法有更快的收敛速度；以优化测点优化结果为现场贴片指导，利用无线应变检测仪检测8个测点，8个测点分别对应1～8通道，检测结果与仿真结果接近。该研究结果对后续主轴装置故障诊断以及主轴装置载荷检测的研究提供了数据基础。