基于蒙特卡洛方法的三体船侧体运动响应优化

王硕 ，宗智*

1大连理工大学船舶工程学院，辽宁大连116024

2高新船舶与深海开发装备协同创新中心，上海200240

3辽宁省深海浮动结构工程实验室，辽宁大连116024

0 引言

三体船作为一种高性能船舶，具有快速性好、耐波性优良、稳性及抗沉性高等优点，发展前景良好。最常见的三体船型，其水下部分由1个主体和2个侧体共3个细长船体组成，2个侧体通过连接桥与主体连成一体［1］。

船舶的运动性能是船舶设计的一个重要指标，国内外学者对此展开了大量研究。宗智等［2］基于“三维移动脉动源法”计算了三体船的运动，发现侧体位置对三体船的运动性能有重要影响，并分析了具有良好耐波性的布置方案；马山等［3］采用二维半势流理论对三体船在斜浪规则波中的运动响应进行了预报。郑律等［4］应用计算软件TRIMARAN研究了侧体纵向、横向位置变化对三体船运动响应的影响，并针对不同航速提出了侧体优化方案。冯炎鑫［5］采用Wasim分析了在主船体和侧体主尺度相同的情况下，不同侧体位置布置对三体船运动性能的影响。姜宗玉等［6］运用HydroStar软件对在横向规则波中航行的三体船进行了数值计算，发现其横摇性能主要受侧体横向位置的影响。李培勇等［7］针对三体船的横摇性能进行了试验研究。Hebblewhite等［8］通过模型试验，研究分析了三体船侧体纵向位置改变对其运动响应的影响。吴乘胜等［9］采用CFD方法，针对侧体纵向位置变化对三体船水动力性能的影响进行了研究，并提出了耐波性优良、波浪增阻较小的水动力方案。贾敬蓓等［10］针对三体船运动性能进行了模型试验，结果表明，侧体位于主体舯前能明显改善三体船的运动性能。

以上研究表明，三体船侧体位置的布置对三体船的运动性能影响很大，因此在设计时，存在着三体船侧体布置的运动性能优化问题。从理论上讲，由于侧体位置有无穷多种方案，故有必要研究能有效计算三体船侧体布局对优化运动性能影响的技术。本文拟基于蒙特卡洛方法和势流理论，提出一种三体船侧体布局对船舶运动影响的优化方法，给出多目标的优化模型和计算技术，并通过一艘三体船的例子来说明该方法的实用性。

1 优化方案

本文将“后三体船”作为原始船型（即侧体位于主体艉部，船舶运动响应较大），并记为S0方案。在一定范围内，通过改变侧体的纵向和横向位置，采用蒙特卡洛方法来选取方案进行优化，从第1种到第n种依次记为S1～Sn方案。在规则波中，不同方案的三体船横摇运动响应RAO峰值为R(Si)、纵摇运动响应RAO峰值为P(Si)、升沉运动响应RAO峰值为H(Si)；在实际海况中，波浪为不规则波，记不同方案三体船的横摇幅值为r(Si)，纵摇幅值为p(Si)，升沉幅值为h(Si)。若某种方案Sn的3个指标同时达到最小，即

同时满足，则表示优化船型Sn可以减小三体船的运动响应，也即在运动性能上优化了三体船。

1.1 蒙特卡洛方法确定多组侧体布置

在三体船中，侧体位置的取值是无穷的，而采用蒙特卡洛方法则可以在合理的范围内找到全局最优解，同时也可减少计算量［11］。方案产生步骤如下：

1）确定侧体位置的合理区间。

侧体位置的区间如图1所示。其中，坐标系原点o取在主船体船艉中点处，xoy平面位于设计水线面上，x轴指向船艏为正，y轴指向船体左舷为正，z轴垂直于xoy平面，向上为正。侧体与主体之间的纵向距离为a，即侧体艉部到主体艉部的距离，其取值范围为［0，63］（即船艉至船艏）；横向距离为b，即主体纵向中心线与侧体纵向中心线之间的距离，其取值范围为［12，17］（即原始船型侧体位置至远离船体5 m的距离，5 m为侧体在水线处宽度的3倍）。

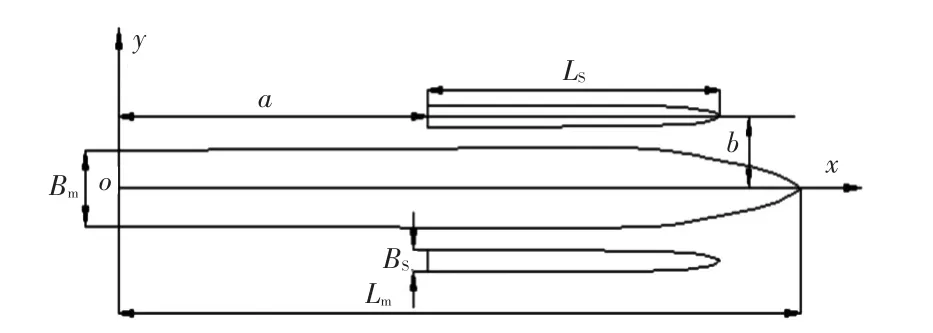
图1 三体船侧体布置图Fig.1 The sketch of trimaran side-hull layout

2）采用线性同余法产生“伪随机序列”以确定具体方案。

线性同余法是产生“伪随机序列”最简单的数学方法，其递推公式为

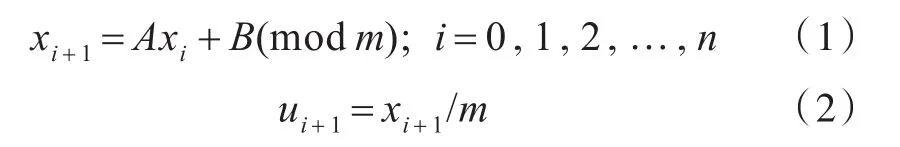
式中：模数m、乘数A以及初始值x0（种子）均为正整数，且m＞0，m＞A，m＞x0，其中m，A的选取保证随机数周期大、相关性小；B为增量，通常取B=0。通过线性同余法，产生了一系列A，B值用于进行数值计算，取其中的5组作为例子列于表1中。

表1 三体船侧体方案参数Table 1 The parameters of trimaran side-hull layout

采用这种方法产生的随机序列已经过均匀性及独立性检验［11］，这里不再赘述。

1.2 数值计算

本文运用AQWA商用软件研究了侧体位置改变对三体船运动性能的影响，并通过比较进行了优化。AQWA软件主要用于解决浮体在环境载荷作用下的运动响应、系泊定位、海上安装作业、船舶航行以及波浪载荷传递等方面的问题［12］，其基本理论为三维势流理论，即假设流体为理想流体，无旋、无粘性且不可压缩。本文以图2所示的三体船作为计算模型，其主尺度如表2所示。

图2 本文中的三体船示意图Fig.2 The sketch of trimaran in this paper

表2 三体船的主要船型参数Table 2 Main parameters of the trimaran

侧体布置方案理论上有无穷多种，本文只给出了6种（表1）。每种布置方案分别计算5种浪向，分别是迎浪、首斜浪、横浪、尾斜浪和顺浪，如图3所示。

1.3 试验验证

姜宗玉等［6］在进行三体船横摇性能研究时，将计算结果与试验数据进行了对比验证，结果显示吻合良好，这表明多体夹缝间流动对数值计算影响很小，数值计算结果准确、可靠。

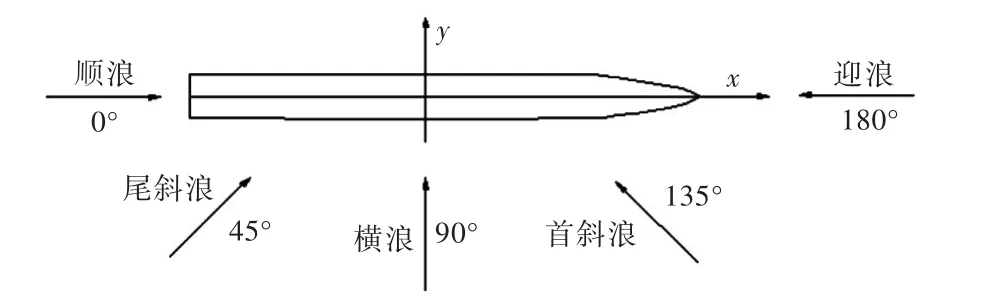
图3 浪向示意图Fig.3 The sketch of wave directions

2 计算结果及分析

2.1 规则波下的运动响应

本文将以S0～S5这6种侧体布置方案为例，给出其频率响应函数。

2.1.1 横摇运动响应

6种方案在不同浪向角下的横摇运动曲线如图4～图9所示。图中，横坐标为波浪遭遇频率ω，纵坐标表示三体船在频率ω、波幅1 m的规则波作用下所产生的角度或位移（用RAO表示），μ为浪向角。

图4 S0方案下的横摇运动响应曲线Fig.4 The curves of trimaran roll RAO for S0

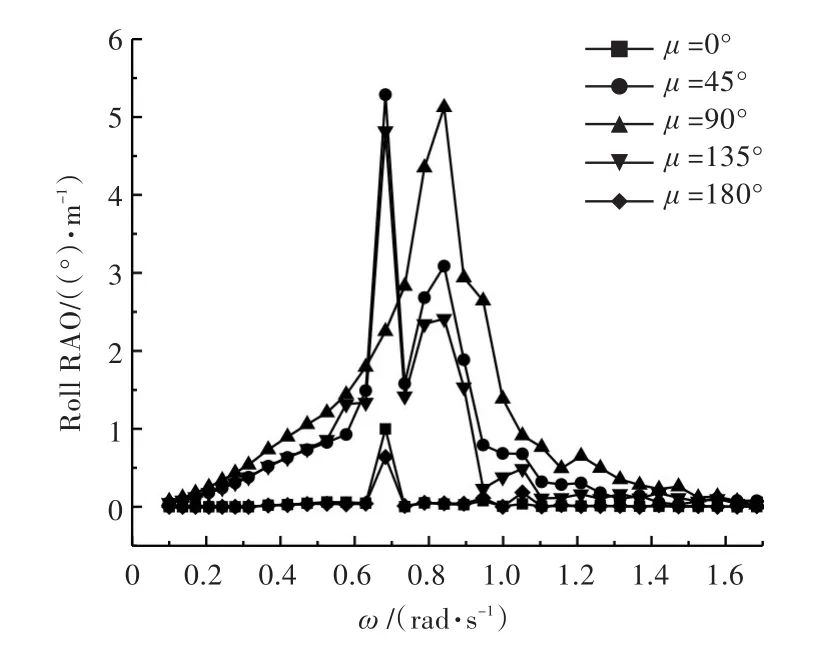
图5 S1方案下横摇运动响应曲线Fig.5 The curves of trimaran roll RAO for S1

由图4～图9可以看出：R（S5）＜R（S3）＜R（S0），表明S3和S5这2种优化方案可以减小三体船的横摇幅度，其特征为侧体纵向位置靠近船艏，横向位置远离船舯。

图6 S2方案下的横摇运动响应曲线Fig.6 The curves of trimaran roll RAO for S2

图7 S3方案下的横摇运动响应曲线Fig.7 The curves of trimaran roll RAO for S3

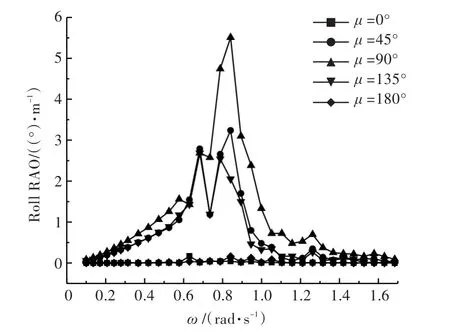
图8 S4方案下的横摇运动响应曲线Fig.8 The curves of trimaran roll RAO for S4

图9 S5方案下的横摇运动响应曲线Fig.9 The curves of trimaran roll RAO for S5

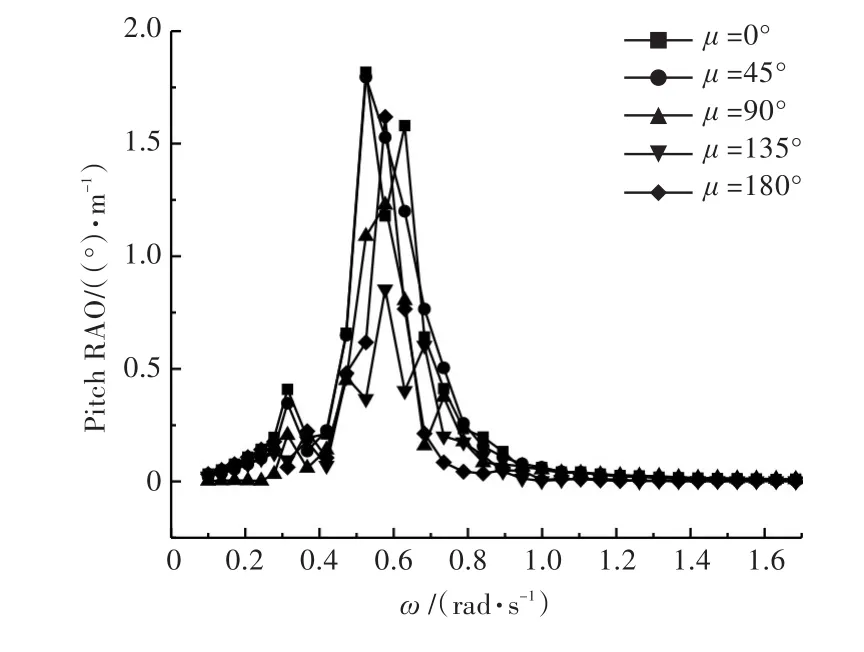
图10 S0方案下的纵摇运动响应曲线Fig.10 The curves of trimaran pitch RAO for S0

图11 S1方案下的纵摇运动响应曲线Fig.11 The curves of trimaran pitch RAO for S1

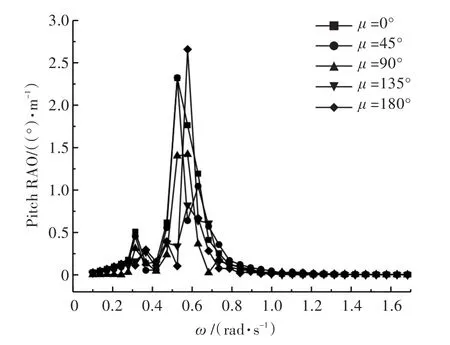
图12 S2方案下的纵摇运动响应曲线Fig.12 The curves of trimaran pitch RAO for S2

2.1.2 纵摇运动响应

图10～图15给出了6种方案在不同浪向角下的纵摇运动曲线。

由图10～图15可以看出：

1）纵摇运动响应RAO峰值大致出现在浪向角为0°或180°时，这表明三体船在迎浪和顺浪状态下纵摇幅度较大；

2）P（S1）＜P（S3）＜P（S4）＜P（S0），这表明侧体靠近主体舯部附近可以有效减小三体船的纵摇幅度。

图13 S3方案下的纵摇运动响应曲线Fig.13 The curves of trimaran pitch RAO for S3

图14 S4方案下的纵摇运动响应曲线Fig.14 The curves of trimaran pitch RAO for S4

图16 S0方案下的升沉运动响应曲线Fig.16 The curves of trimaran heave RAO for S0

图17 S1方案下的升沉运动响应曲线Fig.17 The curves of trimaran heave RAO for S1

图18 S2方案下的升沉运动响应曲线Fig.18 The curves of trimaran heave RAO for S2

图19 S3方案下的升沉运动响应曲线Fig.19 The curves of trimaran heave RAO for S3

2.1.3 升沉运动响应

图16～图21给出了6种方案在不同浪向角下的升沉运动曲线。

从图16～图21中可以看出，H（S4）＜H（S3）＜H（S5）＜H（S0），这表明 S3，S4和 S5这 3种方案可以减小三体船的升沉幅度，而这3种方案的侧体均靠近船艏，表明“前三体船”对升沉运动的响应有着明显的改善作用。

综上分析，在规则波中，S3方案能同时减小三体船的横摇、纵摇及升沉运动响应，即当侧体位于三体船主体舯前位置，并同时增大侧体与主体之间的横向距离时，可以减小运动响应。

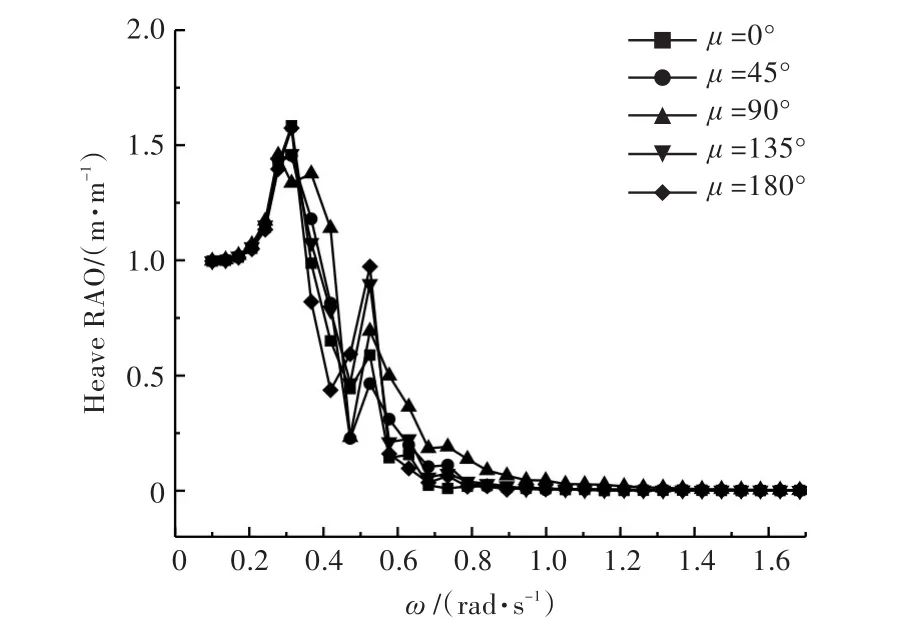
图20 S4方案下的升沉运动响应曲线Fig.20 The curves of trimaran heave RAO for S4

图21 S5方案下的升沉运动响应曲线Fig.21 The curves of trimaran heave RAO for S5

2.2 不规则波下的运动响应

本文选取渤海海域波浪谱计算不规则波下三体船的运动响应，波浪谱为P-M谱［13］：

式中：HS为有义波高，HS=3.4 m；，为谱峰处角频率，其中TP为谱峰周期，TP=8.4 s。该波浪谱对应的响应谱为假设随机波浪是窄带的各态历经过程，则船体在随机波中的响应为［14］

对响应谱进行积分，即可得运动的有义统计值（1/3值）为：

据此，得到计算结果如表3所示。

表3中的数据表明：在不规则波中，S3方案和S5方案的横摇运动响应最小，表明当侧体位于主体舯前，同时增加主体与侧体之间的横向距离时，可以改善三体船的横摇性能；S1，S3～S5方案的纵摇运动响应均小于原始方案，表明增加主体与侧体之间的横向距离可以改善三体船的纵摇性能；升沉运动响应的变化不大。

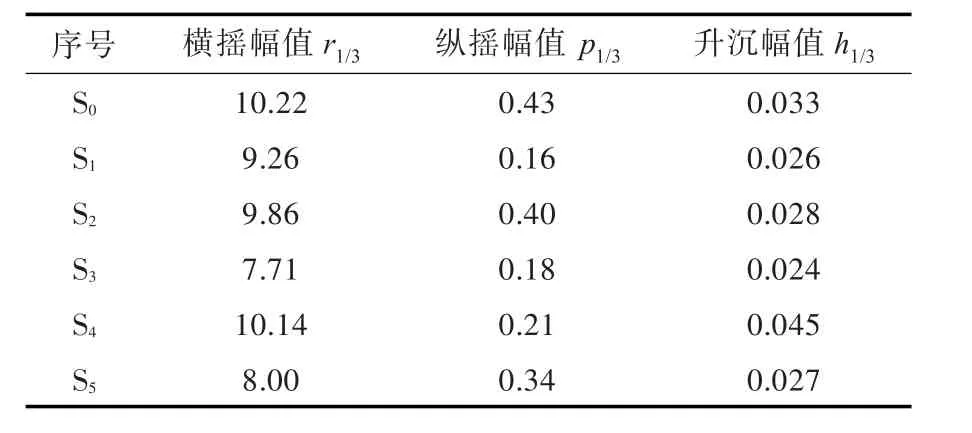
表3 摇荡幅值计算结果Table 3 results of amplitude

3 结 语

本文运用蒙特卡洛方法选取三体船侧体布置方案，并使用AQWA软件（势流理论）计算了不同侧体方案的三体船在规则波及不规则波中的运动响应。计算结果表明，当侧体位于主体舯前位置时，同时增加主体与侧体之间的横向距离,可以改善三体船的运动性能，这与文献［10］的模型试验结果一致。