浅谈小学数学教学中怎样渗透化归思想

毛丽

【摘要】化归不仅是一种重要的解题思想，而且是一种最基本的思维策略，更是一种有效的数学思维方式。所谓化归思想方法，就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化，进而达到解决问题的一种方法。

【关键词】渗透;化归思想;切入点;活动;能力

在小数数学教学中渗透化归思想非常重要。笔者从事小学数学教学十几年，收获很多，下面就针对小学数学教学中化归思想的渗透谈一谈体会。

一、找好切入点，渗透化归思想

在小学数学教学中，化归思想的利用很多。如教小学一年级学生认识20以内的数的时候，将10根小棒捆成一捆，当作10，教师可以发散：“2捆呢？3捆呢？……”再如“囗+○=Δ”，“Δ”代表5，“囗”代表1，填一填“○”代表几，等等。教师在引导学生思考的时候，自己首先就要明白这是一种数学思想的渗透。

如，在分数的加减法中，异分母化为同分母就是“化繁为简”“化新为旧”。在教学的时候不要停留在教材的练习上，可以设计比较分数大小的练习，可以化成分母相同比较分子，也可以化为分子相同比较分母，这样学生就有了多种方法，这也是化归思想中的“化模糊为明朗”。再设计拓展训练“”，开发学生的思维，提示学生可以从分母上思考，也可以从分子上思考，还可以化为小数后再思考。这样学生思考的余地就很大，学生的思维一下子就被打开了。所以，教师体会了化归思想后，就可以更好地理解这类训练的目的和意义，让训练更具有针对性。

在教学小学生解决求简单未知数的值的时候，刚开始遇上形如“”这样的式子时，学生会很难理解，如果教师心中有化归思想，就会设计为“4个Δ+一个Δ，一共几个Δ”或者是“4框梨子加上一筐梨子共有几框梨子”。这样就使抽象数学问题形象化、生活化。其实这就是化归思想的“变抽象为形象”。其中的“x”既可以代表“Δ”，也可以代表“一筐梨子”，还可以代表……这样学生不仅解决了难题，而且对未知数或者字母代替数有了更直观的认识。

又如“某同学买4本书、7支笔用了61.8元，买2本书、3支笔用了28.5元，求每本书、每支笔多少钱？”教师引导：因为同样的书和笔的单价不会改变，通过“买2本书、3支笔用了28.5元”可以得到“买4本书、6支笔用了28.5×2=57元”，再利用已知“买4本书、7支笔用了61.8元”，明显多出61.8-57=4.8（元），这4.8元就是一支笔的单价，从而可以顺利地计算出每本书的价格。

二、利用一些活动课，渗透化归思想

小学数学课中有很多活动课，学生有了化归思想的意识，就能把复杂的数学问题变成简单的问题，从而轻松地解决。

例如，在学习了“求长方体的体积、正方体的体积、圆柱体的体积”后，让学生求一块不规则铁块的体积，当学生用切割法、拼接法都不好解决的时候，可以让学生用橡皮泥做成铁块大小，然后将橡皮泥捏成圆柱体或长方体或正方体，把问题转化;也可以给学生一杯水，让学生想办法。这时学生的思维一定能得到启发，办法也就多了，可能会有学生提出让工匠把这块铁打成长方体、正方体或圆柱体等等。这样，学生解决问题的能力得到了提升。

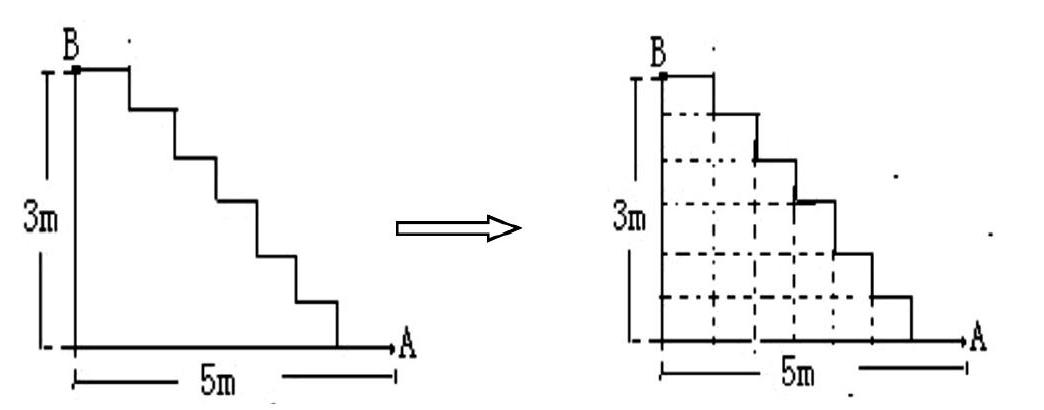
再如，某饭店为了在楼梯A到B上铺一层防滑的垫子，有关的尺寸如下图，请你帮助店主计算一下，他该去买多长的防滑垫？

这道题学生如果没有一些数学思想的渗透，解决起来不是那么容易。如果用化归思想引导，即将每个階梯的地面平移到地面，阶梯的立面平移到墙面，你会发现什么？同学们一下就明白了。这里就用到了“变曲为直”的数学思想，也蕴含了用平移的方法解决几何问题，为今后的学习打下了基础。

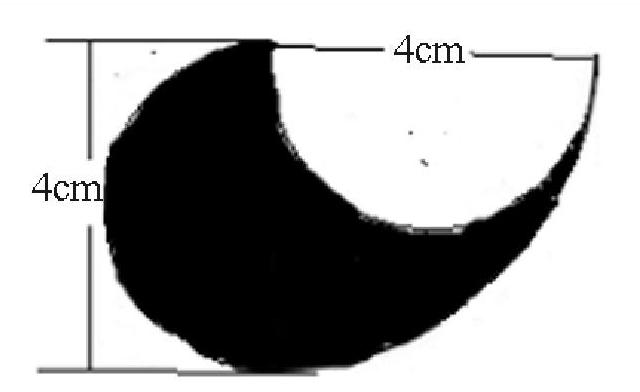
在小学数学中，学习了圆的面积后，利用圆的面积求不规则图形的面积时，可以设计如下例题，组织活动训练学生思维。如何求如图阴影图形的面积？

教师利用多媒体动画，将图形旋转拼图，引导学生思考，如果将图甲绕A点旋转就会转化拼图为图乙，同学们一下就明白了：旋转四次就刚好与原图形重合，旋转的轨迹是一个半径为4cm的圆，阴影部分的面积为图乙圆面积的四分之一。

这道训练题利用旋转拼图的方法，将未知图形变成了学过的已知图形圆的问题，从而变得更加简单易懂，既渗透了化归思想，又传递了可以用旋转的方法研究几何问题，同时培养了学生的图形变化能力。

综合上述，在小学数学教学中，数学思想的渗透很重要，有了数学思想，教师教学的目的性更强了，把握教材更精准了，设计练习更灵活了，针对性会更强。有很多教师教书还勉强可以，但是设计练习题，层次不清楚，选题难，就是缺乏数学思想。在数学教学中培养学生的科学素养，也就是从数学思想和数学方法中去落实的。笔者通过小学数学中化归思想的渗透来说明数学教学中数学思想的重要性，目的是抛砖引玉，让更多的教师在数学教学中重视数学思想的渗透和应用。古人云“授之以鱼不如授之以渔”，就是这个道理。

【参考文献】

[1]叶军荣.如何在小学数学教学中渗透数学思想方法[J].数学学习与研究，2016（02）.