自正则检验Gamma分布的变点问题

谭景宝，夏道明

(合肥幼儿师范高等专科学校基础部，安徽合肥 230013)

1 研究背景

变点问题在统计应用中很常见，广泛应用于工业质量控制、医药统计、生存分析、气象生物学以及金融经济等领域.如果一个序列存在变点，则在变点前后，模型将会发生变化.如果忽略变点的存在，则会对统计推断产生很大的影响，甚至会得出错误结论.目前，多参数变点问题在统计推断中越来越受到关注，但是研究文献却十分有限，以往的研究主要集中于均值或者方差变点的研究，本质上这两个参数是无关的，但是在Gamma分布中，均值和方差同时依赖于形状参数和尺度参数.因此研究Gamma分布变点问题显得尤为重要[1].本文主要研究Gamma分布变点问题在股市连涨连跌收益率方面的应用.通常关于股票收益率的研究重点在于每日收益率随时间变化的波动规律，但是从实际情况来看，股票的当日收益率对日后收益率的影响并不显著.本文主要研究股票指数连涨连跌收益率的变化规律.股票指数的连续上涨和下跌可以看作是一种生存过程，当股指连续上涨到头转为下降时，可以看作是上涨的死亡，反之亦然，股指就是在这两种状态下不停地进行“生死”相互转换的.国内最早对这一课题进行研究的有雷鸣等[2].

迄今为止，股市上的变点研究已经取得一些成果.雷鸣[3]利用生存分析和极限理论对上证指数进行研究，指出股指连涨连跌收益率服从Gamma分布，且不同时期分布参数不同.谭常春[4]将Gamma分布变点问题引入股市连涨连跌收益率的变化情况中，指出股指收益率中国股市发展呈现出“政策市”特点.叶五一[5]通过分析高频连涨连跌收益率的相依结构以及CVaR估计，验证了股指上涨和下跌的不对称性以及杠杆效应.胡心瀚[6]使用Copula-ACD模型和条件VaR方法拟合股票的连涨连跌收益率的边缘分布和联合分布，结果表明拟合效果优于传统方法.黄飞[7]运用Bayes分析对上证指数连涨连跌收益率变结构问题进行研究.研究股市收益率的变点问题，可以在一定程度上规避损失.

2 Gamma分布变点问题

假设X1,X2,…,Xn为来自Gamma分布的独立随机变量序列，满足：

Xi～Gamma(v,λi),i=1,2,…,n.

其概率密度函数为：

其中，v为形状参数，λ为尺度参数.

典型的Gamma分布变点问题存在两种情况：(1)假设形状参数不变，刻度参数的变点问题(Hsu，1979)；(2)假设刻度参数是已知或未知的常量，形状参数的变点问题(Lorden & Pollak，2005；Ramanayake，2004；Tan，Zhao & Miao，2007)[6].

本文研究Gamma分布两参数的变点问题，判断Gamma分布序列形状参数和刻度参数是否分别存在变点，即进行如下假设检验：

(2)刻度参数变点检验：H0:λ1=λ2≡λ，H1:λ1≠λ2.

其中，v1、v2分别为变点前后Gamma分布的形状参数，λ1、λ2分别为变点前后Gamma分布的刻度参数.

3 自正则检验

3.1 形状参数的变点研究

谭常春[1]在Shao[8]的基础上，对其提出的检验统计量进行改进，定义一个新的检验统计量Gn，来检验变点前后模型参数是否相同.下面给出检验统计量：

①

3.2 刻度参数的变点研究

本文在谭常春[1]给出的形状参数检验统计量的基础上，对Tn(k)稍作改变，可得到刻度参数检验统计量：

其中，

4 K-S分布检验

Kolmogorov-Smirnov检验(K-S检验)基于累积分布函数，用于检验一个经验分布是否符合某种理论分布或者比较两个经验分布是否有显著性差异.

H0：总体服从某一连续分布F；H1：总体不服从某一连续分布F.

本文中利用K-S检验来验证不同阶段的收益率序列是否符合Gamma分布.因此当原假设H0为真时，收益率序列服从Gamma分布.

5 在金融序列中的应用

5.1 连涨连跌收益率

5.1.1 连涨连跌收益率计算方式

雷鸣[3]在研究中指出，股票的连涨连跌收益率服从Gamma分布.由此使用自正则检验对股票连涨连跌收益率的变点问题进行研究.

由于上证指数最能代表中国股票市场，因此选取2006年1月4日至2016年12月30日共计2673个上证指数的数据研究形状参数的变点问题.

上证指数收盘价趋势图如图1所示.

图1 上证指数收盘价趋势图

连涨连跌收益率是在每日收益率的基础上计算的.连涨(跌)收益率是指这2673个交易日收盘价每次开始上涨(下跌)到上涨(下跌)结束时的收益率之和.通过计算，一共得到669个连涨收益率和668个连跌收益率.为操作方便，在下面的分析中，将连涨收益率和连跌收益率分别记为X和Y.运用R软件可得连涨连跌收益率数据如表1所示，趋势图如图2和图3所示.

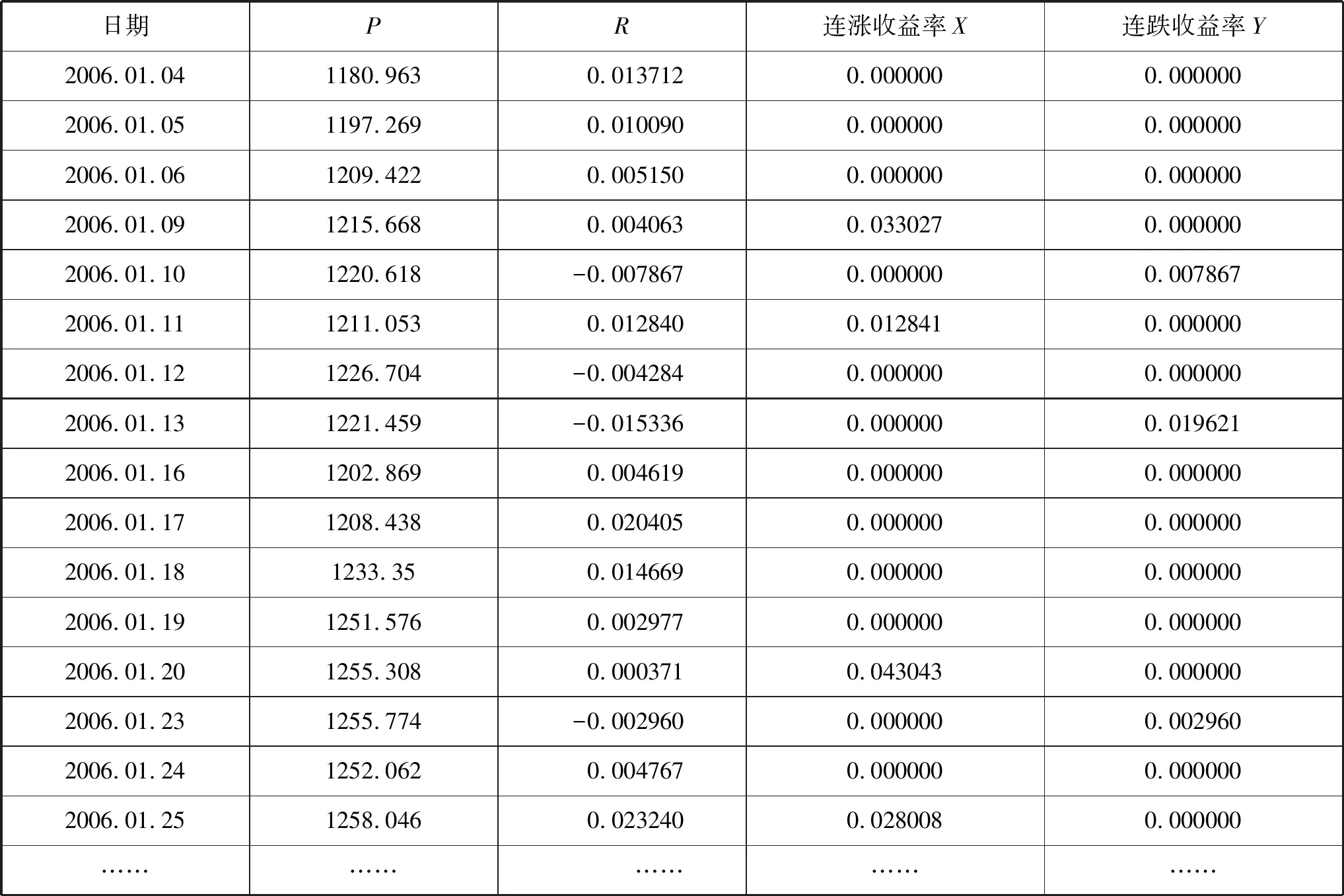
表1 2006.01.04—2016.12.30连涨连跌收益率

注：篇幅有限，省略2006.01.26至2016.12.30数据.

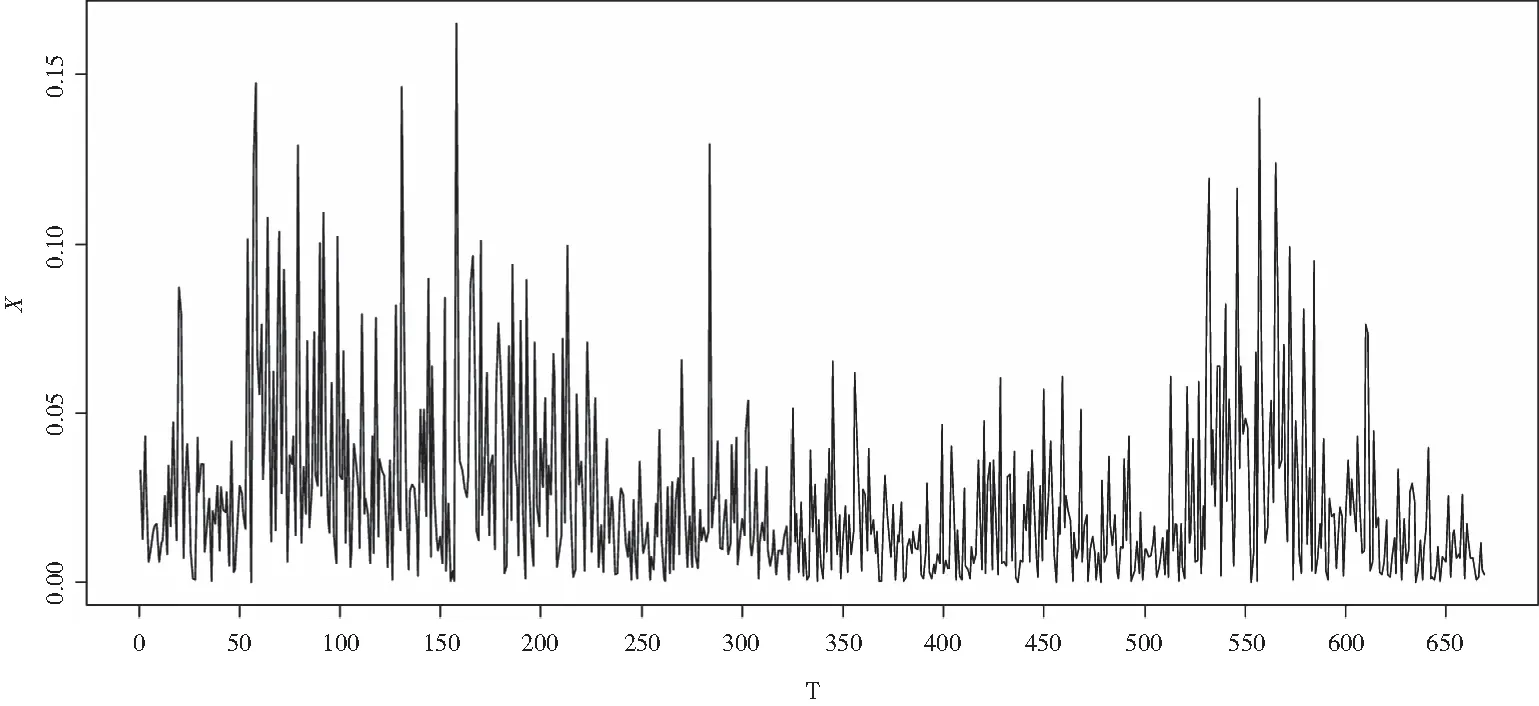
图2 上证指数2006.01.04—2016.12.30连涨收益率

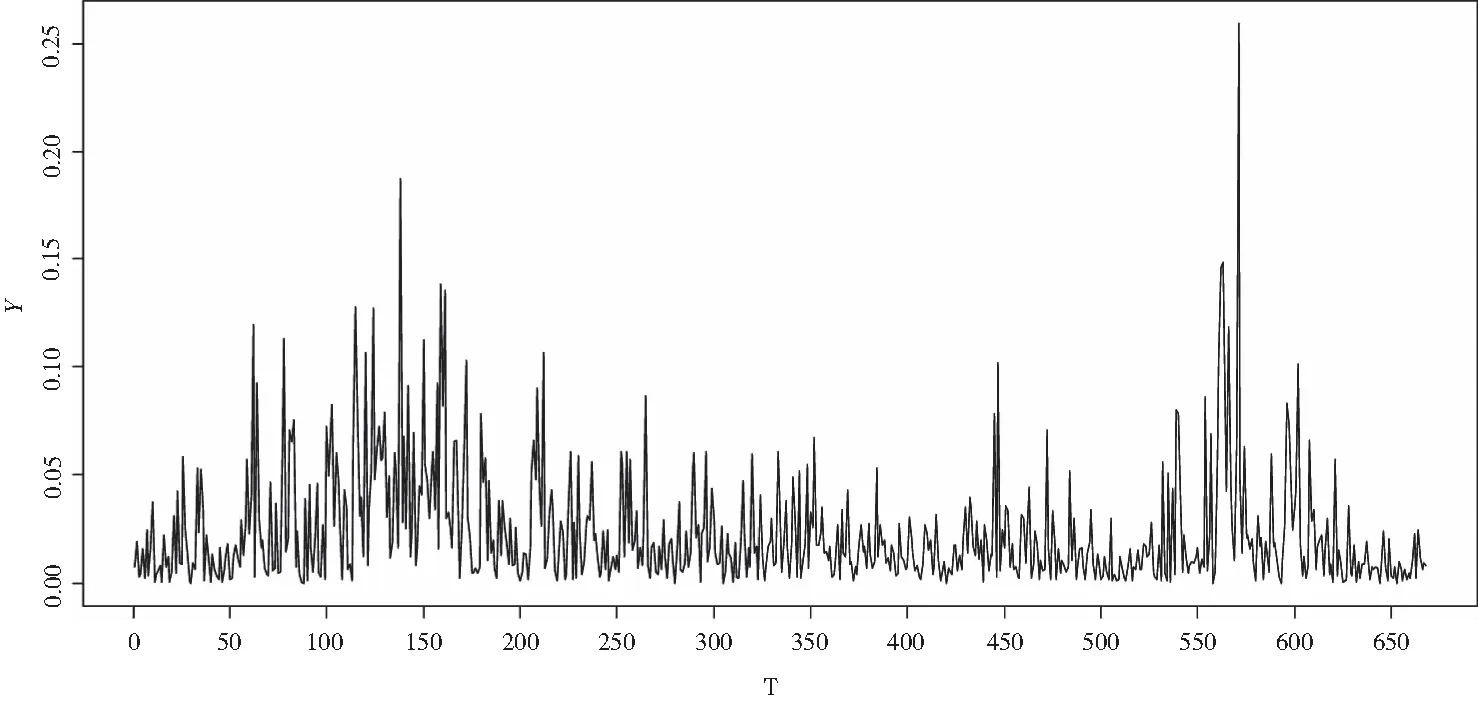
图3 上证指数2006.01.04—2016.12.30连跌收益率

在此期间，很多重大事件的发生影响了中国股市的发展，股市波动起伏不断，经历过多次牛市和熊市.政府为股市的平稳健康发展，先后出台过一些政策，如四万亿投资计划(2008年11月11日)等.这些重大事件和政策影响了股票市场的每日收益率的涨跌.这些影响的程度如何，是否会导致连涨连跌收益率发生结构性的变化？下文将会对此进行进一步研究.

5.1.2 连涨连跌收益率序列分布拟合

5.1.2.1 连涨收益率

图4 连涨收益率序列直方图及密度函数曲线

由图4可知，连涨收益率序列近似服从Gamma分布.利用K-S检验进行验证.P值为0.4078，大于0.05，不拒绝原假设，则说明连涨收益率序列服从Gamma分布.

5.1.2.2 连跌收益率

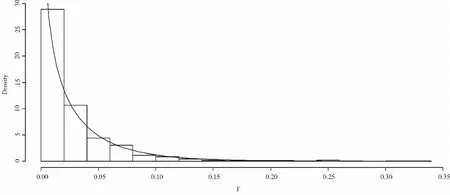
图5 连跌收益率序列直方图及密度函数图

由图5可以看出，连跌收益率序列近似服从Gamma分布.利用K-S检验，得到P值为0.9141，大于0.05，所以说明连跌收益率序列服从Gamma分布.由上述分析可知，上证指数连涨连跌收益率服从Gamma分布，与雷鸣[9]的分析结论一致.下文使用Gamma分布变点的研究方法分析沪指连涨连跌收益率.

5.2 形状参数变点估计

根据①式，对上证指数连涨连跌收益率进行分析，可得连涨连跌收益率第一个变点(表2).其中通过模拟检验计算不同置信水平下的检验临界值为C(0.05)=43.5，C(0.1)=26.5.

表2 上证指数连涨连跌收益率第一个变点

上证指数连涨收益率Gn图如图6所示，上证指数连跌收益率Gn图如图7所示.图中第一条横线代表置信水平为0.05的临界值C(0.05)=43.5；第二条横线代表置信水平为0.1的临界值C(0.1)=26.5.

图6 上证指数连涨收益率Gn图

图7 上证指数连跌收益率Gn图

由表2、图6和图7可知，连涨收益率第一个变点在2010年2月附近，而连跌收益率变点发生在2012年7月附近.下面使用二分法对变点前后的数据再次分析，可得连涨连跌收益率形状参数变点估计结果(表3).

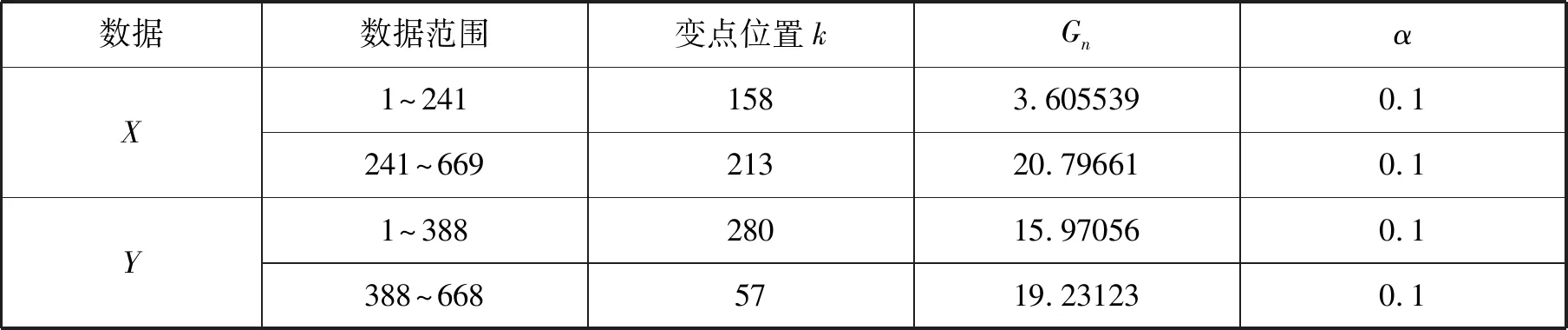
表3 连涨连跌收益率形状参数变点估计

下面给出分段检验的Gn图(图8至图11).

图8 上证指数连涨收益率1～241的Gn图

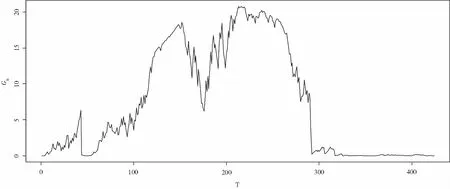
图9 上证指数连涨收益率241～669的Gn图

图10 上证指数连跌收益率1～388的Gn图

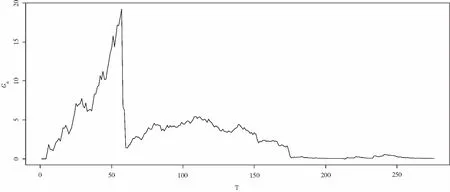
图11 上证指数连跌收益率388～668的Gn图

由表3以及图8至图11可知，上证指数连涨收益率在1～241和241～669中不存在显著变点.连跌收益率在1～388及388～668中亦不存在显著变点.下面继续使用二分法分段检测变点，均未发现其它显著变点，故检测结果如表3所示.

表2为运用自归一化检验和二分法估计连涨连跌收益率的多变点的结果.选取显著性水平为分别是α=0.05,α=0.1，临界值分别为C(0.05)=43.5,C(0.1)=26.5.连涨和连跌收益率序列各存在一个显著变点.连涨收益率变点发生在2010年7月附近，2009年我国相继推出十大产业振兴计划，刺激了相关行业个股大幅上涨.而后区域振兴规划更为相关板块上市公司形成利好刺激.10月底创业板的推出，为市场提供了新的利好机会，促进了2010年股市的发展.连跌收益率变点发生在2012年7月.2012年1月至4月在政策的刺激下，股市探底随后强烈上扬，从5月8日起开始连续下跌7个月.

5.3 刻度参数变点估计

选取1992年5月21日至2016年12月30日共计6009个上证指数的数据(舍去1992年5月21日以前的数据是因为在此前后的上证指数编报方法不同，无法放在一起进行比较)进行研究刻度参数的变点问题.

利用R软件对连涨连跌收益率序列进行变点估计，结果如表4和表5所示.其中通过模拟检验计算所得的不同置信水平下的检验临界值C(0.05)=346411.9,C(0.1)=245229.1.

表4 连涨收益率刻度参数变点估计

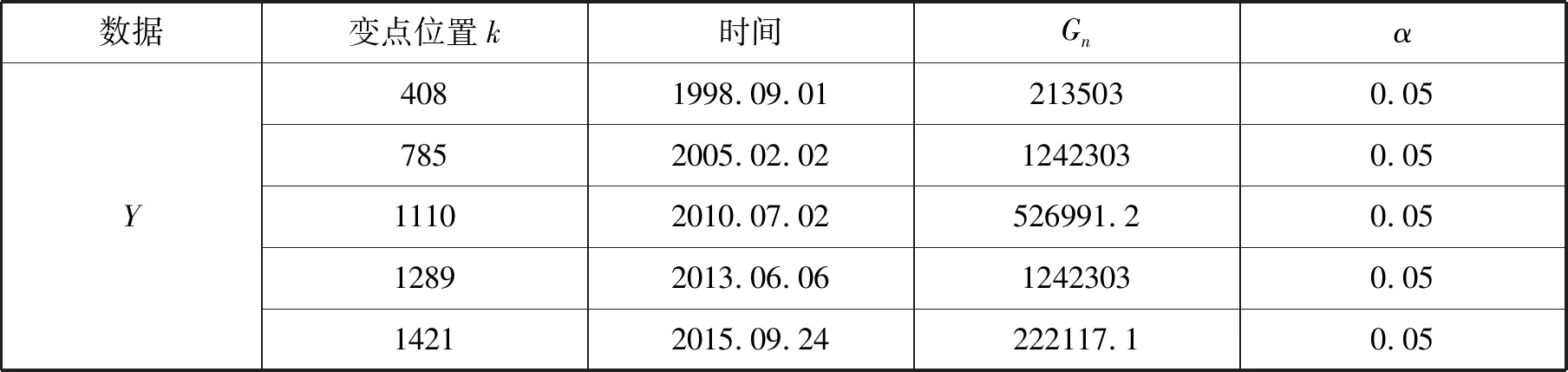
表5 连跌收益率刻度参数变点估计

表6 连涨收益率各阶段序列分布检验

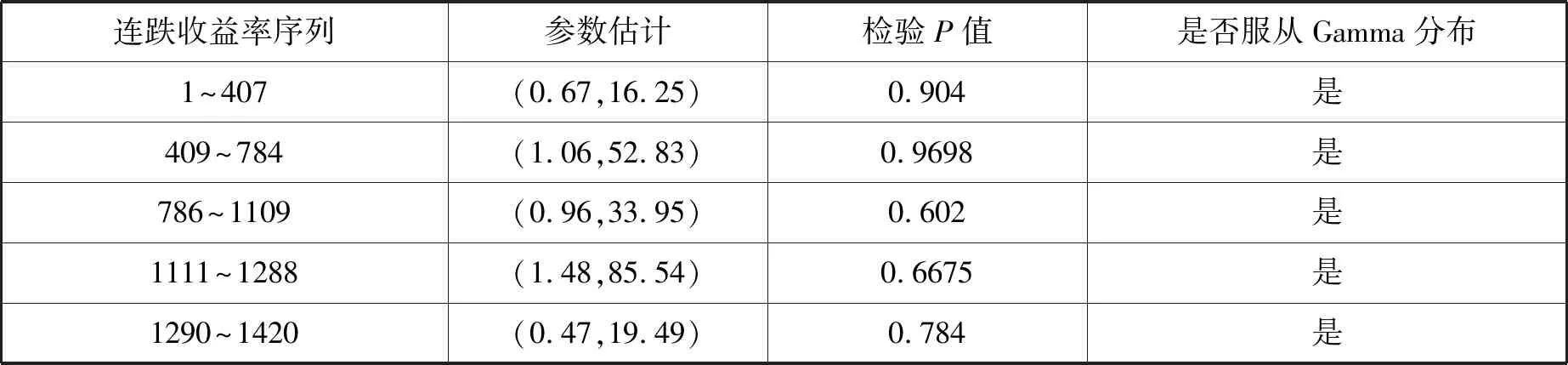
表7 连跌收益率各阶段序列分布检验

由表4和表5可知，连涨收益率序列4个变点，连跌收益率序列一共有5个变点.相较于形状参数，刻度参数对股市的变动则表现地更加敏感.由表6和表7可知，连涨连跌收益率变点之间的序列均符合Gamma分布.

5.3.1 连涨收益率变点分析

第一个变点在1998年2月，1997年7月香港回归以及东南亚金融危机对我国股市产生了深远的影响.第七个变点在2002年9月，2001年6月“国有股减持”实行对2002年的股市产生了显著影响.第十一个变点是2014年6月，2014年深化体制改革全面启动，美国宽松货币政策全面退出，使得中国股市迎来新一轮的牛市.最后一个显著的变点在2016年的4月初，2016年IPO新股申购新规、注册制的实施、熔断机制以及人民币贬值和大股东减持对股票市场影响巨大.

5.3.2 连跌收益率变点分析

对比表4和表5可知，1998年连涨收益率、连跌收益率结构均发生变化.连涨连跌收益率均会受到我国大事件及股市政策的影响，说明我国股市具有“政策市”的特点.有别于连涨收益率序列，连跌收益率则更容易受到政策和重大事件的影响.

沪指连跌收益率在2005年2月存在的一个显著变点，2005年股权分置改革，且2005年处于本次大牛市的起始点，促使2006年和2007年成为牛市，表明其波动性发生改变.第三个显著变点发生在2010年，2009年国家进行十大产业调整振兴计划，这一利好消息极大促进了股市的发展.但2010年融资融券、股指期货获批，造成市场恐慌，股市大跌.第四个变点在2013年上半年，2012年欧洲股市危机、国内经济下滑以及领导人换届等国内外环境使得股票市场不明朗，2013年上半年也受到影响，6月触底.最后一个显著变点发生在2015年9月，2014年全面深化改革和央行再次降息对市场产生巨大影响.2015年6月开始，由于场外配资清理、场内融资和分级基金去杠杆形成连锁反应，股市出现暴跌，主要集中在6月中旬到8月底.

6 结语

本文在谭常春[1]自正则检验Gamma分布形状参数变点的基础上，将其自正则检验统计量运用到金融问题中，研究上证指数连涨连跌收益率的变点.得到以下结论：第一，上证指数连涨连跌收益率序列均服从Gamma分布，当股市受到重大事件及政策的影响发生变化时，Gamma分布的参数也会随之改变.第二，上证指数连涨连跌收益率分布中形状参数和刻度参数均容易受到我国政策的影响，具有“政策市”的特点.但相较而言，刻度参数则对市场的变化反应更加强烈.第三，股市的政策对连涨连跌收益率序列的影响具有时滞性.