线膛身管有限元网格参数化建模方法

邹利波，于存贵，郭昭蔚，冯广斌

(1. 南京理工大学 机械工程学院, 江苏 南京 210094； 2.中国船舶重工集团七一三研究所, 河南 郑州 450015)

身管是提供火炮内弹道过程的基础部件，承受极高的火药气体压力。弹丸发射过程中，弹丸与身管膛线发生相互挤压，弹带材料经历高瞬态大变形、摩擦等过程[1]。弹丸在膛内运动是一个高度非线性问题。研究弹丸膛内起始运动过程，对于研究弹丸运动规律有着重要意义[2-6]。随着科学技术的发展，有限元方法逐渐成为研究该类问题的主流方法。在有限元模型中，身管有限元网格的构造和网格精度对仿真计算结果的准确性尤为重要。

线膛身管的内膛结构复杂，受载恶劣。使用有限元分析方法时，需要对身管进行有限元网格离散。大口径火炮身管大都为线膛身管，膛线的截面几何尺寸较小，且绕身管轴线螺旋旋转。影响身管有限元网格的建立和优良单元的划分。

目前，对于身管结构畸形有限建模，大都是首先在三维软件中建立身管三维实体模型，然后导入网格前处理软件(ANSA、Hypermesh等)中，最后导入有限元软件中进行计算。如丁传俊等[7]提出了基于Python语言的“分片拼接”方法构造了身管的网格模型，但是该方法在一定程度上较为复杂，不能快速建立身管模型，且不能建立包含药室、坡膛和身管外部轮廓的有限元网格模型。张振辉[8]通过计算膛线控制点的坐标，然后根据控制点的坐标在建模软件中生成膛线曲线，再将此曲线导入Hypermesh软件中建立单根膛线，操作过程同样复杂。杨国来等[9-10]将身管切割成多段，并建立身管有限元模型，同时建立了弹丸与身管之间的接触碰撞模型，研究弹炮匹配问题。吴会民等[11]在三维建模软件中建立身管的实体模型，导入前处理软件ANSA中，生成单根膛线，然后旋转，贴合节点，形成身管有限元网格模型。过斌等[12]通过选用非均匀有理B样条基函数建立分块的身管三维等几何模型，并将其合并成完整的膛线身管几何模型。这些文献中各个软件数据的相互导入，不仅将导致操作烦琐，而且容易导致数据丢失，且花费时间较长，网格模型精度较差。

为探索快速有效的精确建立身管结构有限元网格模型，本文基于有限元仿真软件ABAQUS的脚本语言Python对身管结构(含药室、坡膛结构)进行参数化建模，提出了一种基于Python脚本语言操作单元和节点坐标的身管参数化建模方法，来建立身管有限元网格模型。该方法能够精确建立身管内膛(包含药室、坡膛和导向部)和身管外部轮廓的有限元网格模型。

1 身管参数化建模

火炮身管内膛由药室、坡膛和导向部等部分组成，如图1所示。其中导向部包含膛线结构，对有限元网格建模而言相对较为复杂。Python是一种模块化的程序扩展语言，功能强大，可独立于程序，也可用于脚本程序。通过Python语言调用库函数，可以直接操纵ABAQUS内核，实现建模、划分网格、制定材料属性、提交作业等操作[13]。在商业软件ABAQUS的基础上，提出一种利用Python语言进行身管有限元网格参数化建模的方法。具体操作方法如下：

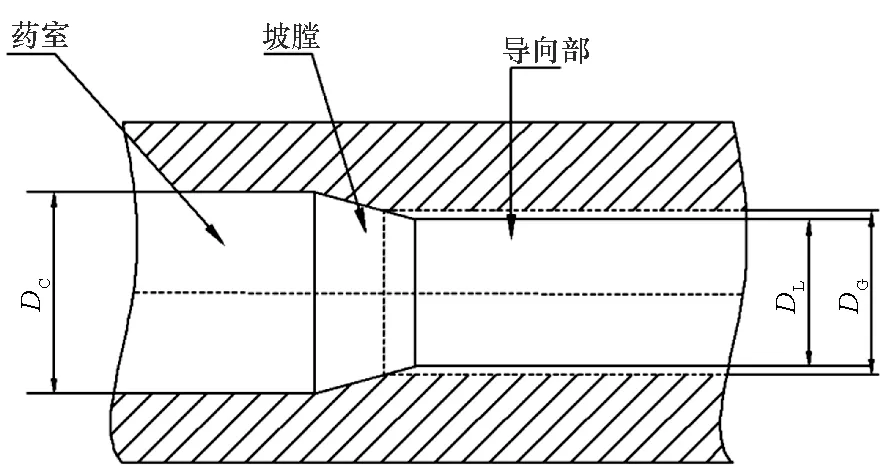
图1 火炮内膛结构示意图Fig.1 Schematic of gun bore

1)根据身管内膛结构实际尺寸，在ABAQUS软件中，按照如图2所示的中心小圆(直径为阴线宽度)方法，建立火炮身管膛线截面。并拉伸身管截面，形成直圆柱的身管。对直圆柱火炮身管划分网格，如图3所示。

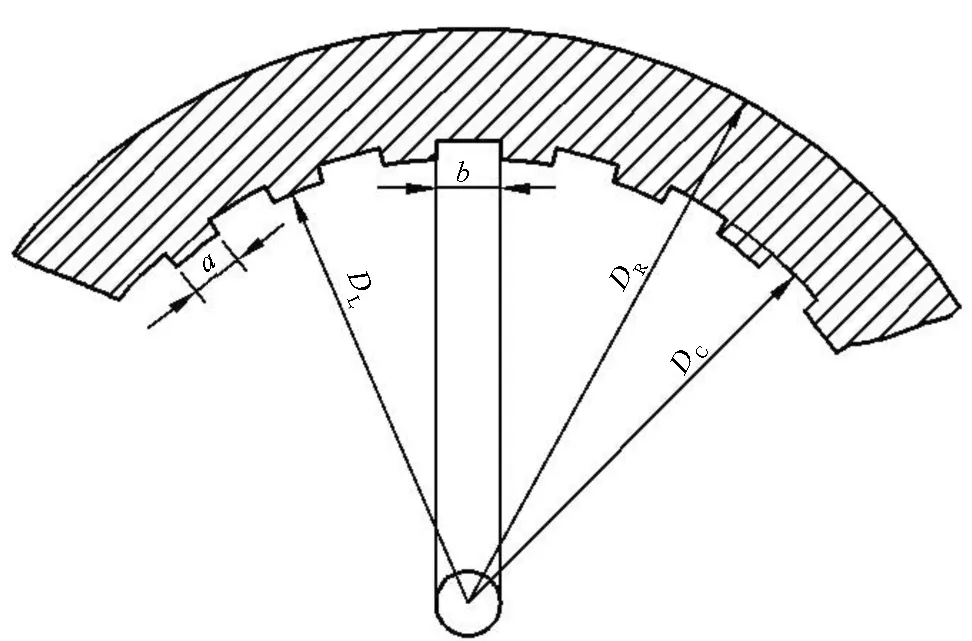
图2 身管膛线结构示意图Fig.2 Schematic of gun land and groove

图3 直圆柱身管网格有限元模型Fig.3 Finite element grid of straight gun tube

2)在生成直圆柱身管网格的过程中，ABAQUS软件自动生成一个执行日志文件(.rpy)，几乎每一步操作都可以在该文件中找到对应的语句。将该文件名后缀改为Python脚本程序文件(.py)，形成Python脚本语言，并将身管结构参数使用变量代替，以方便进行参数化建模。[14]

3)生成包含单元和节点的Inp文件，利用Python语言读取Inp文件中包含的沿身管轴线每一层单元的节点坐标。例如，如图4所示，利用身管每一层单元的前后端面节点的z方向坐标相同，定位到膛线起始部单元(假设第3层单元为膛线起始部单元)，将靠近炮尾方向的端面节点作为源面节点，另一端面节点作为终面节点。识别单元的源面节点和终面节点后，将源面节点作为不动点，终面节点作为偏移节点。单元节点偏移原理如图5所示，如在该单元中，节点100、101、102、103为源面节点，节点200、201、202、203为终面节点，源面节点到终面节点为身管轴向方向。节点偏移时，以节点203为例，节点203是该单元终面节点之一，也是另外一个单元源面节点之一，将此节点根据身管缠度和膛线形式进行偏移，根据同一个圆上的一点203(x，y)旋转任意角度后，由式(1)可获得偏移后的新坐标203(x′，y′)，即完成该层单元的节点偏移，如图6所示。

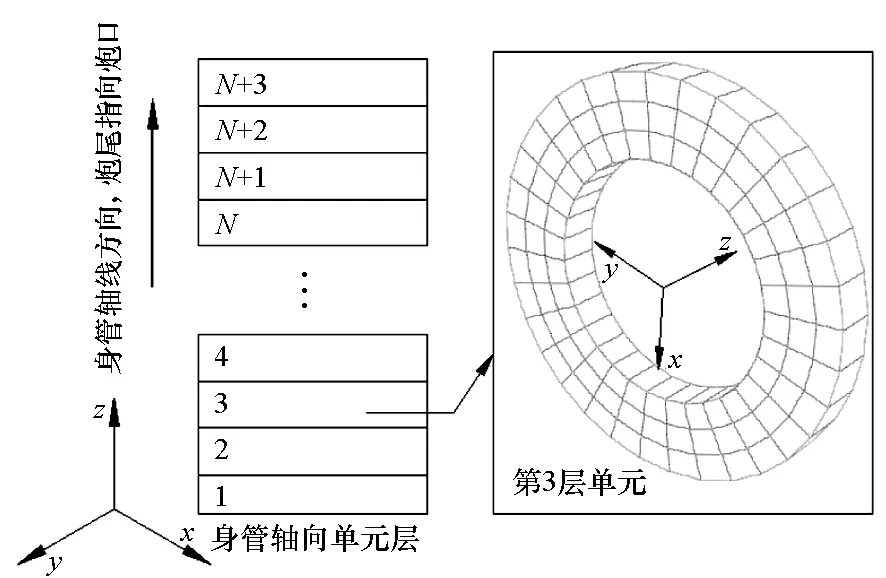
图4 单元层识别示意图Fig.4 Schematic of elements distinguish

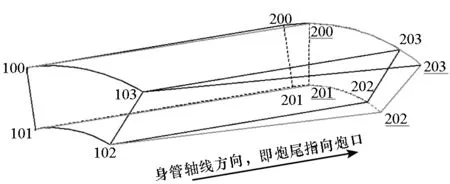
图5 单元节点偏移原理Fig.5 Principle of node-offset algorithm

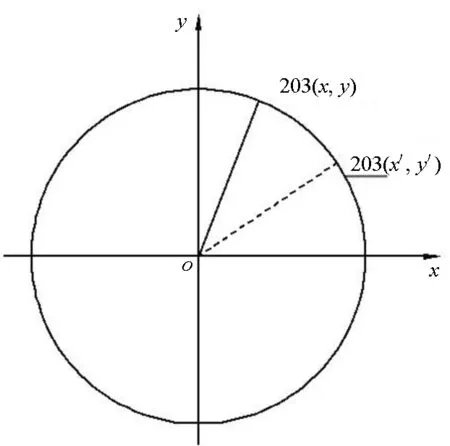
图6 节点偏移计算示意图Fig.6 Schematic of node-offset algorithm

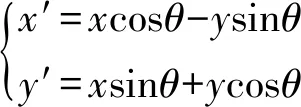
(1)

4)将修改后的节点坐标导入新的Inp文件中，即形成身管有限元网格模型。图7所示为使用该方法生成的76 mm火炮身管有限元网格模型。

详细操作流程如图8所示。使用该方法可以生成任意膛线形式、缠角和坡膛结构的身管有限元网格模型。利用Python语言编写该方法，程序编写简单、快速，且生成身管的时间只有几秒左右。

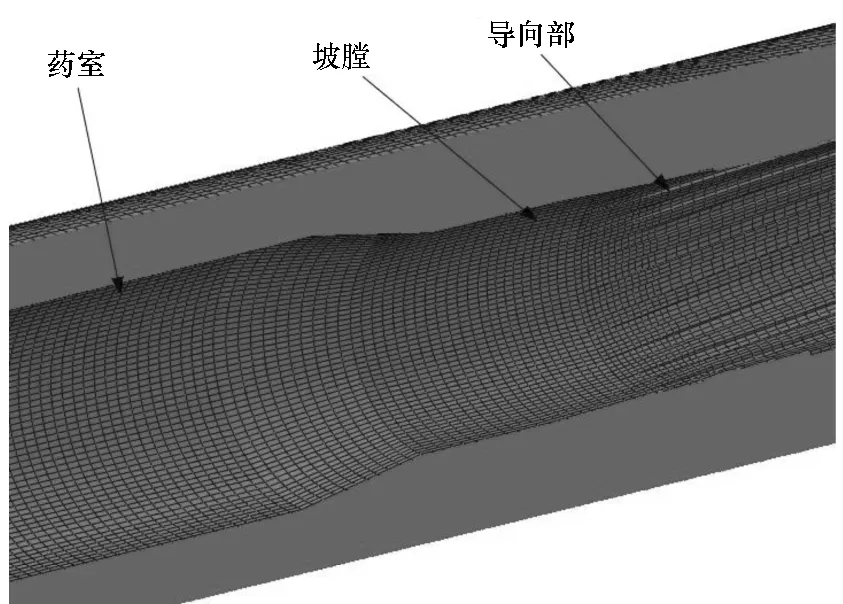
图7 身管有限元网格模型(剖视图)Fig.7 Finite element grid of gun tube(section view)

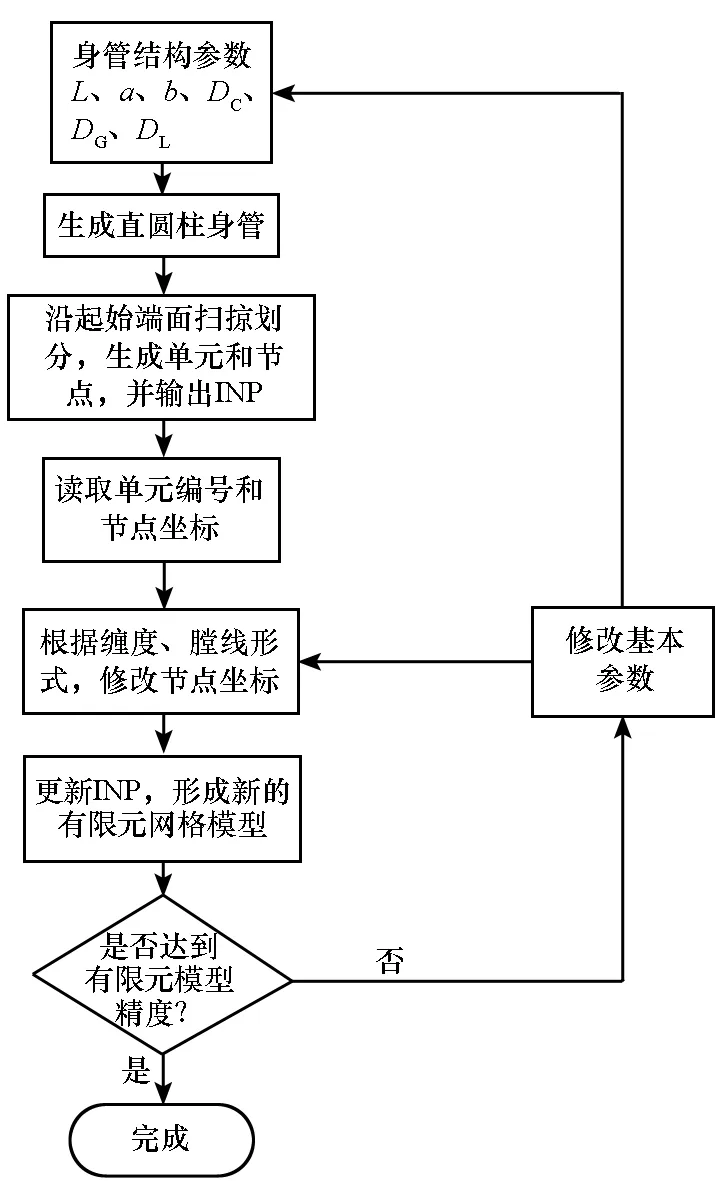
图8 程序操作流程图Fig.8 Flow chart of procedure

2 模型验证及其结果分析

为了验证以上方法生成的身管有限元网格模型的正确性，使用该方法生成76 mm火炮身管有限元模型，并建立弹丸与身管耦合的有限元模型。

2.1 有限元网格

以76 mm火炮身管为研究对象，在有限元模型中，对身管几何结构进行相应的简化。采用C3D8R减缩积分单元，对弹带、身管坡膛起始的网格进行了细化。弹带与弹体采用“tie”绑定约束。弹丸定心部与阳线、装药与弹体内部采用面与面接触，建立了弹带与身管内表面以及弹体与阳线表面的接触碰撞模型。弹丸在挤进膛线过程中，弹带内部网格会不断暴露，因此弹丸与身管内表面的接触设置为“自接触”模型。图9为弹丸有限元网格模型局部示意图，图10为弹炮耦合有限元模型。

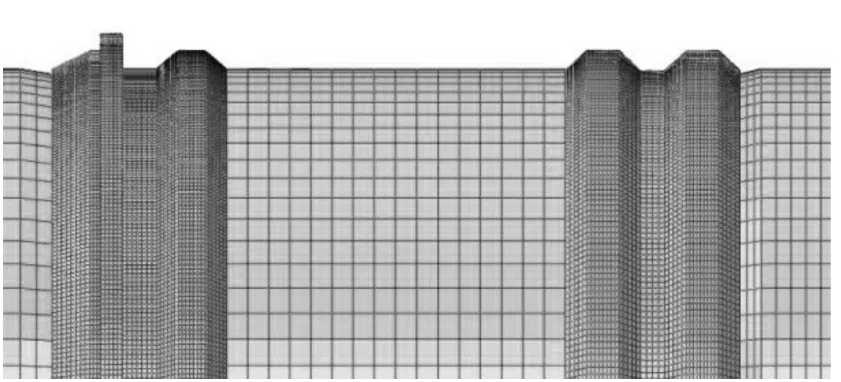
图9 弹带有限元网格模型Fig.9 Finite element grid of local projectile

图10 弹炮耦合有限元模型Fig.10 Finite element of projectile-barrel interaction

在有限元模型中，做出如下假设：

1)弹丸卡膛姿态与身管轴向一致；

2)不考虑身管的后坐运动和弹丸前端气体动力的影响；

3)不考虑温度对弹丸挤进过程的影响。

2.2 材料模型

弹带材料为黄铜，身管材料为炮钢。弹丸在挤进过程中经历弹塑性变形及损伤，最终发生局部化韧性断裂，涉及弹带材料的应变硬化、应变率硬化和温度软化，Johnson-Cook适合描述大部分金属材料[15-16]，故采用Johnson-Cook本构模型及其失效本构模型，其表达式分别为：

(2)

(3)

(4)

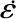
2.3 载荷和边界条件

重力载荷作为常值加载在模型中，弹丸底部施加拨弹力和弹底压力，其中拨弹力大小为60 kN，作用时间约为1 ms。发射药采用正装药，弹底压力按由内弹道计算获得的压力-时间曲线施加在弹带后端面上。身管尾部端面固定约束。

2.4 计算结果分析

计算完成后对结果进行分析，可以看出弹带在身管阳线的挤压下形成凹槽痕。图11为76 mm火炮弹丸实际弹带变形图，和回收的实弹相比弹带变形情况基本一致。

图11 实际弹带变形图Fig.11 Deformation of practical bearing band

图12(a)、图12(b)、图12(c)和图12(d)所示，分别为计算得到的弹丸在膛内运动过程中的弹丸位移-时间、速度-时间、加速度-时间和角速度-时间曲线。

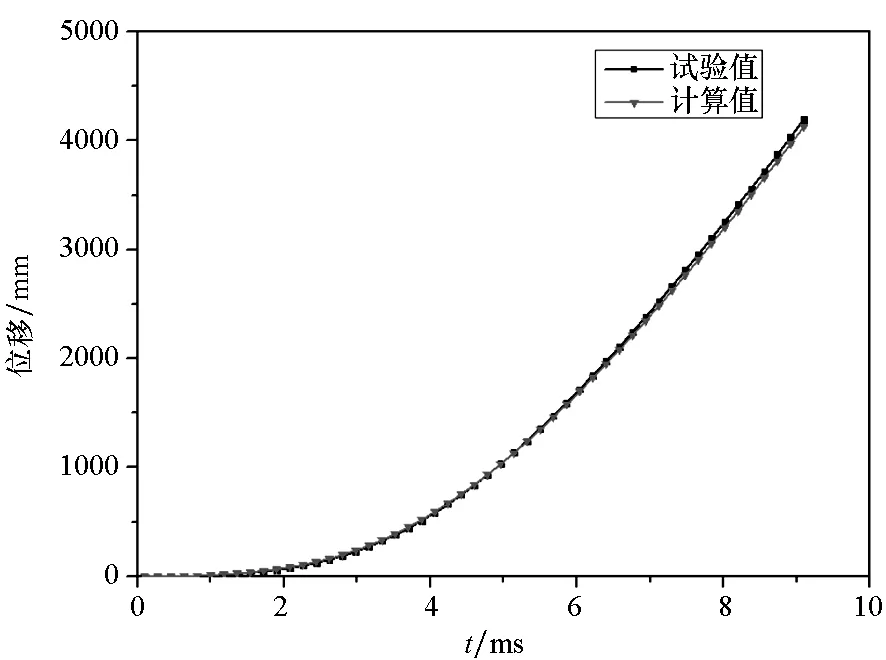
(a) 弹丸轴向位移与时间关系曲线(a) Axial displacement of projectile with time

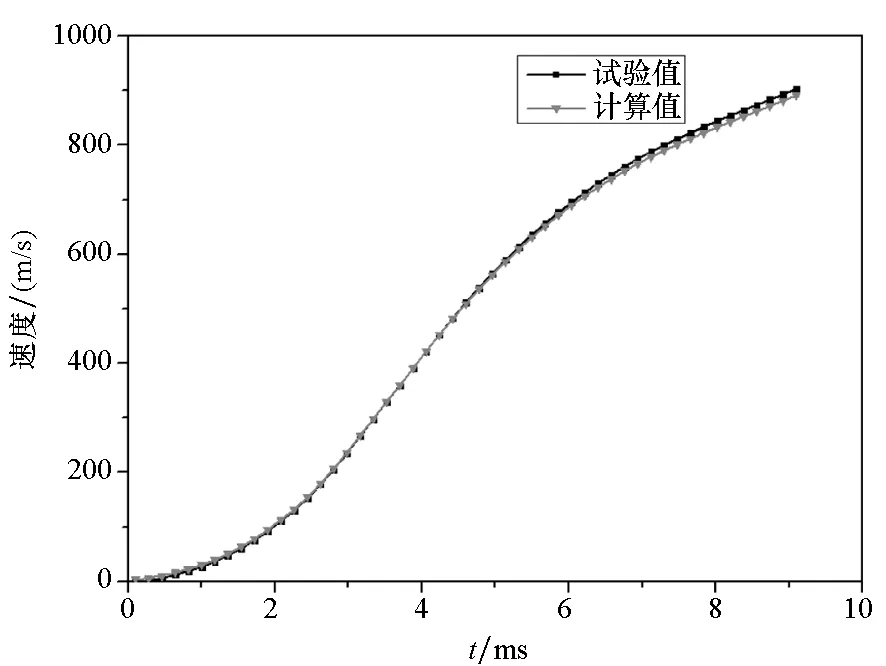
(b) 弹丸轴向速度与时间关系曲线(b) Axial velocity of projectile with time

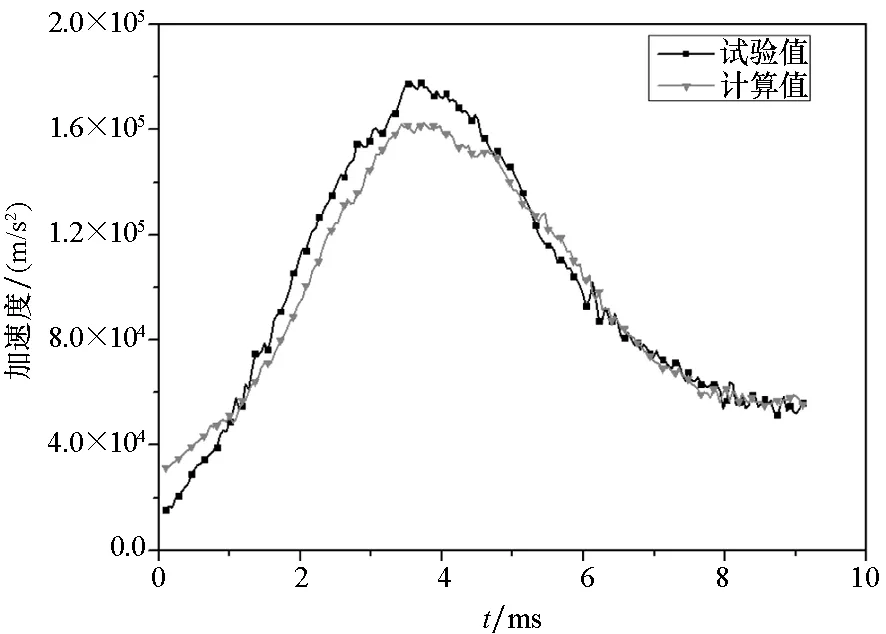
(c) 弹丸轴向加速度与时间关系曲线(c) Axial acceleration of projectile with time

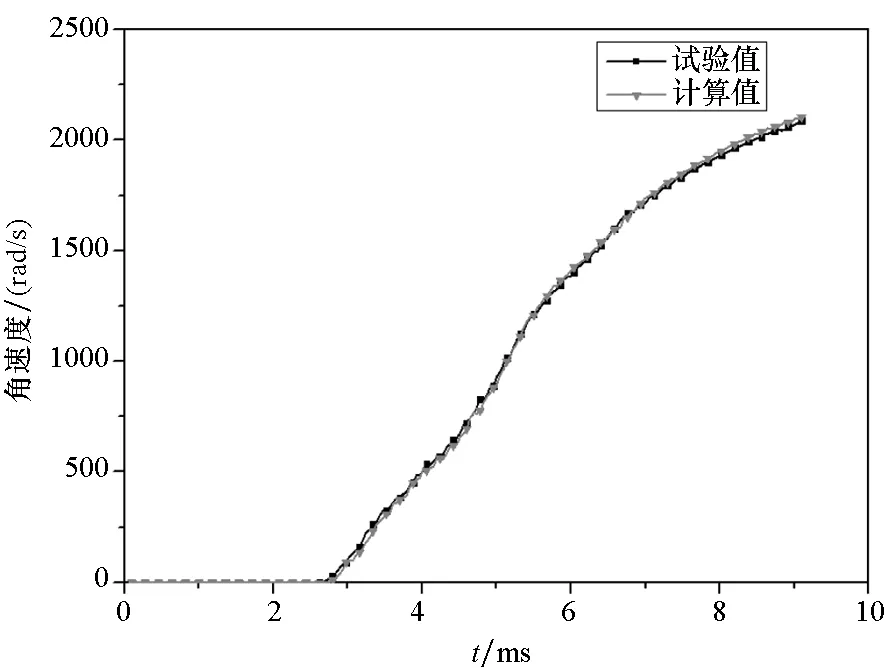
(d) 弹丸轴向角速度与时间关系曲线(d) Angular velocity of projectile with time图12 弹丸运动曲线Fig.12 Curve of projectile

由图12(a)可知，弹丸出炮口时刻约为8.5 ms，与实际弹丸出炮口时刻基本一致。由图12(b)可知，计算得到的弹丸出炮口速度约为946 m/s，与实验测得到的弹丸出炮口速度965 m/s相差较小。图12(c)为计算获得的弹丸沿轴向加速度，最大膛压时刻的加速度大小为1.6×105m/s2，与实验值相差8.2%。图12(d)为弹丸沿身管轴向角速度随时间变化关系，弹丸出炮口时刻角速度约为2212.569 rad/s，试验测得的弹丸出炮口角速度为2146.405 rad/s，误差较小。由于有限元建模过程中未考虑弹带软化的影响，弹丸开始旋转时刻较试验值早一点。经以上分析可知，建立的身管有限元网格模型精度较好。

3 结论

基于有限元仿真软件ABAQUS的脚本语言Python，提出了一种参数化建立身管有限元网格模型的新方法。该方法在有限元单元和节点坐标上进行操作，能够快速、精确建立身管内膛(包含药室、坡膛和导向部)和身管外部轮廓的有限元网格模型。以76 mm火炮身管为对象，建立了身管与弹丸耦合的有限元模型，仿真计算弹丸在膛内的全弹道运动，获得了弹丸出炮口时刻的位移、速度和加速度随时间变化的曲线，计算获得的结果与实验结果基本一致，表明使用该方法建立的身管有限元网格模型的准确性和精度较好。