例谈不同数学课型化归思想的教学实践与探索

官莉萍

（福建省福州市岳峰中心小学，福建福州 350011）

引 言

思想方法是数学的精髓，在学生学习数学知识时，教师应注重向学生渗透数学思想方法。这样，学生在掌握表层知识的同时，还能领悟深层思想方法，从而举一反三，触类旁通，自主建构知识体系，以便启迪智慧，提升思维，这是数学学习的最终目的。基于以上思考，笔者分别就新授课、复习课、练习课如何充分利用化归的数学思想方法进行了探索。

一、新授课——化新为旧

对于学生而言，学习过程是一个不断面对新知识的过程。新授课主要教授新的定义、例题、定律、原理等，而大多数新知识与旧知识存在一定的联系，因此，学生可以充分利用已有知识，通过探索，把新知转化为旧知进行学习[1]。

例如，在教学《口算两位数加两位数》时，教师通过创设情境，出示以下口算题，要求学生完成，之后与同桌交流口算思路。

45+30= 52+20= 38+40= 30+35=

72+5= 37+8= 6+44= 58+7=

本节课学习的起点是学生已经学习和掌握了两位数加整十数、一位数的口算方法，复习旧知、回顾方法这一环节的设置旨在帮助学生回忆梳理已有的知识经验，为新知的迁移做了铺垫，从而让学生迅速进入学习状态。

在教授新知的环节中，教师先让学生观察主题图，提出加法问题，学生提出“一年级一共要买多少张车票”时，让学生列出算式：35+34，并用自己的方法进行口算，之后在小组内交流自己的口算思路。学生汇报交流时，思路主要有以下几点：

（1）先算30+35=65，再算65+4=69；

（2）把35 分成30 和5，先算30+34=64，再算64+5=69；

（3）把35 分成30 和5，把34 分成30 和4，先算30+30=60，再算4+5=9，最后算60+9=69。

在复习了旧知的环节之后，教师放手让学生自由运用已学的两位数加一位数、整十数的口算方法，进行两位数加两位数不进位口算的学习，不仅帮助学生系统掌握了计算知识，也培养了学生利用已有知识迁移类推学习新知的能力，同时也为学习口算进位加法做了充分的铺垫。

二、练习课——化生为熟

数学练习课在日常教学中占有相当大的比例，其作用就是促使学生及时消化巩固所学知识，而充分渗透化归思想，上好练习课，化生疏为熟练，能帮助学生把知识与生活经验联系起来，将生活经验转变为深刻的记忆[2]。

例如，在“平行四边形的面积计算”练习课中，教师设计了以下两个环节。

（一）相信我能行

问题1：怎样计算平行四边形的面积？这个计算公式是怎样推导出来的？

问题2：口算以下平行四边形的面积。

（1）底11 米，高8 米；（2）高14 分米，底7 分米；（3）底12.5 厘米，高2 厘米。

通过这两道基本练习，让学生快速回忆巩固前一节课所学知识，为后面的提高练习做好准备。

（二）挑战自我

问题1：一个平行四边形果园底长150 米，高是90 米，它的面积是多少？

（1）学生独立解答，集体订正。

（2）出示：每公顷的收成是6 吨，这块地共可收获果实多少吨？

（3）将问题改为：“一共可收果实8.1 吨，平均每公顷收果实多少吨?”

（3）与（2）比较，从数量关系上看，什么相同？什么不同？

问题2：如图1。

（1）找一找：图中有几个平行四边形？

（2）猜一猜：它们的面积是否相等？

（3）算一算：你找出的平行四边形的面积是多少？

（4）说一说：你能得出什么结论？

通过教师设置的不同类型、不同层次的练习，学生化生疏为熟练，充分掌握了平行四边形面积计算的相关知识，顺利把数学知识与生活经验联系起来，形成深刻的记忆。

三、复习课——化零为整

教师在复习课利用化归思想，将学生所学知识进行转化归纳，把平日分散教学、相对零散的知识进行联系比较，串连成规律性的知识，化零为整，能使学生将新学知识纳入已有的知识系统中，从而形成比较完整的知识体系。

例如，教学六年级下册“平面图形的周长与面积的复习课”时，教师在梳理知识、构建网络环节时进行了以下设置。

师：根据周长的定义，将围成这个平面图形所有的边长加起来就能求出图形的周长了，而面积有这么多个公式，记起来真麻烦，能不能找到它们之间的联系，只记其中一个公式，就能推导出所有的公式，你怎么选择？选择这个公式的理由是什么？

生1：因为正方形是一个特殊的长方形，所以可以用长方形的面积公式；而平行四边形沿高剪下，通过割补、平移可以转化成长方形。三角形与梯形也可以通过类似方法转化成长方形或平行四边形；圆也是把它剪拼转化成长方形从而推导出面积公式的。（幻灯演示）

生2：平行四边形的面积……（回顾面积推导过程），师配合演示。

师：在刚才的整理和推导过程中，我们都是将新图形转化为我们学过的图形进行研究的。可见，转化是解决数学问题的一个重要思想。从上面这些公式的推导过程中你能发现它们之间有什么联系？能把这些图形重新摆一摆吗？

学生汇报并说明：为什么这样摆，怎样摆更合理些。

生：正方形的面积是根据长方形的面积推导出来的，平行四边形的面积是根据长方形的面积推导出来的，三角形和梯形、圆形的面积是根据平行四边形的面积推导出来的。

师生合作形成网络图，如图2。

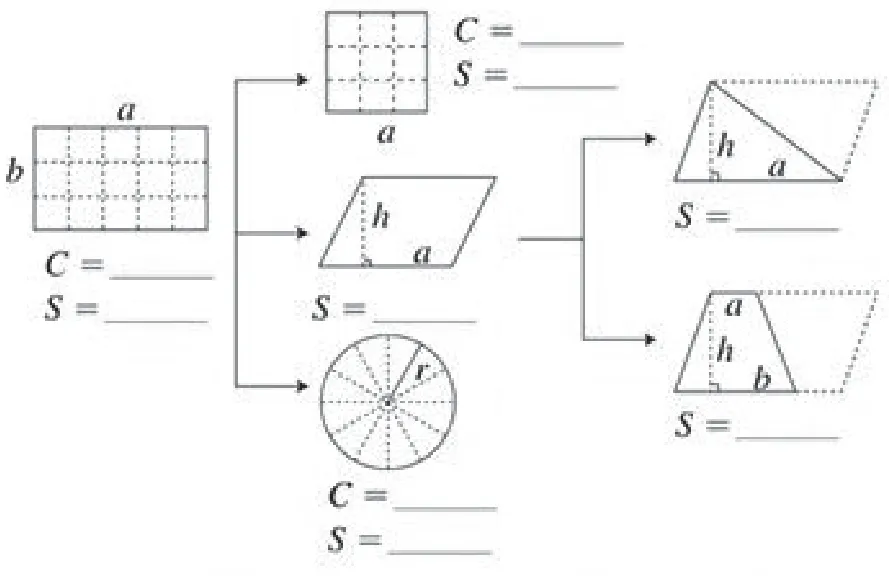
图2

师：大家非常了不起，经过整理复习形成了这样一幅网络图，也叫思维导图。思维导图是一种十分有效的思维模式，是思考、学习、记忆等的思维“地图”。现在请同学们将这幅图逆时针旋转90 度，换个角度看看这幅图竖起来像什么？

生：像一棵知识树。

师：说得真好，图形与图形之间是紧密联系的，长方形的面积计算公式就是树根，是基础，我们可以在这个基础上推导出其他图形的面积公式。

结 语

综上所述，化归思想在数学学习中是一种非常重要的思想，如通过以上将平面图形的面积计算公式条理化、系统化，形成课本上的梳理图，学生系统地感悟了知识的形成过程，从而形成了比较完整的知识体系，也充分体验了数学思想与方法。因此，在实际教学过程中，教师要善于运用化归思想，进而提高教学效率。