关注核心素养 探析课堂教学

康永红

[摘   要]“不等式”是高中数学重要的教学内容，也是数学研究的重要工具.新课标提出要求通过不等式教学使学生能够处理基本的不等关系，初步培养学生的不等观念，提升学生利用不等式知识解决实际问题的能力，促进数学思维的发展.“不等式”教学中，教师应关注基础知识，重视思维发展，倡导应用推广，开展系统渗透，以不断提升学生的核心素养.

[关键词]不等式;核心素养;课堂教学

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）14-0039-02

“不等式”是高中数学的必修内容，是研究基本数量关系的核心知识，在整个中学数学中有着广泛的基础性和工具性，因此新课标要求教师通过该内容的讲解，使学生充分理解基本不等式，并能灵活应用不等关系解决问题.下面笔者结合教学实践进行深入探讨.

一、关注基础知识

数学的基础知识和基本技能是学生核心素养培养的基础，学生的数学思维、数学思想和解题方法均是在理解基础知识的前提下逐步发展起来的.因此，教学不等式内容也应从基础知识入手，引导学生经历知识形成的基本阶段.对于该阶段的教学需要注重两点：一是把握知识的前后联系，完成知识的过渡;二是重视基础定理的推理阐释，完成基础知识的本质剖析.

由于初中生已经对不等式的内容有所了解，所以教师在教学基本不等式时可引导学生重新回顾不等式知识，如不等式的基本性质以及一元一次不等式的解法，具体教学中可以给出几道例题，利用例题引导学生全方位体会不等式运算符号和数值的变化.

在教学的引入阶段应注重基本不等式的引入方式，如对于基本不等式[x2+y22≥xy] （[x≥0]，[y≥0]），虽然可以采取直切主题的方式，但由于学生不了解知识起源和应用指向，所以学习兴趣有所欠缺，教学效果也不太好.数学知识是有一定的实践背景的，不等式也不例外，在教学不等式时十分有必要联系情景问题完成知识过渡，如指明一些不等关系在客观世界是始终存在的;若假定一根线的长度始终恒定，则用该线围成圆的面积会比围成正方形的面积大，而围成正方形面积会比围成一般矩形的面积大.这些问题可以归结为不等式问题，然后引导学生学习相应的基本不等式，并从不等关系角度来加以探究.

而对于第二点的“不等式定理的推理阐释”是强化学生理解的关键，同时通过对定理的推理证明可以提升学生的逻辑推理能力.在该阶段需要由定理和性质的逻辑统一性出发，逐步利用公式之间的相互关系完成证明.在证明过程中除了需要指导学生使用规范的数学语言外，还要引导学生利用不同的分析方法，从不同的角度完成证明，尽可能地培养学生思维的发散性.如证明不等式常用的作差比较法、综合分析法以及基于构造思想的函数构造法等.这些方法的分析思路虽然不同，但对于不等式问题的证明效果是一样的.在教学中加强一题多解的训练，对学生思维的开拓也极为有利.

二、重视思维发展

学生的数学能力决定解题的效率，影响最终的数学成绩，考虑到数学能力的提升与学生的逻辑思维有着很大的关联，因此在教学中教师应特别关注学生的思维活动，利用数学的语言表述和推理活动来锻炼学生的思维.锻炼学生的思维有多种方式，其中最为重要的是强化学生的理解以及帮助学生突破思维障碍.

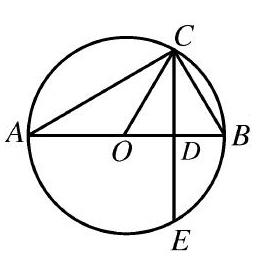
对于不等式基本定理内容的教学，除了需要联系实际问题外，还要借用几何直观来完成过程解释.教学中教师要引导学生基于具体的基本不等式构建几何图像，利用几何直观证明完成定理的学习，从而强化学生对定理的理解.如对于基本不等式[a+b2≥ab] （[a≥0]，[b≥0]），可以構建几何图像，将定理转化为几何问题：如右图，圆O的直径为AB，△ABC为直角三角形，设AD的长为a，BD的长为b，试分析CD与CO的长度关系.具体的思路是：引导学生利用射影定理或三角形相似来构建[CD2=AD·DB，AC2=AD·AB，BC2=BD·BA]，让学生可以直观地得出[CD≤CO]，从而得出[a+b2≥ab] . 这样通过知识的关联来完成定理证明，对学生理解定理有很大的帮助.

高中数学的不等式内容对于学生而言是一块新的知识大陆，必然在学习过程中存在一定的思维障碍，如不理解不等式等号成立的条件、不等式转化变形的基础，以及一些不等式与其他知识交汇问题的分析思路等.教学中教师要善于引导梳理.如对于不等式等号成立的条件探究，可以结合具体的问题将其转化为对应的等式问题，或借助几何知识来完成，在转化过程中要注意对不等式性质的利用，及关注转化过程的符号变化.分析综合性问题时，如不等式与数列综合问题，可以引导学生从不等式和数列关系两个角度进行思考，合理利用放缩法将无规律的不等式和数列转化为规则的数列和基本不等式，并利用相应的性质完成问题的分析证明.

三、倡导应用推广

教学不等式内容时应将“提升学生的应用分析能力”作为教学的重要任务.对于不等式的应用教学，应关注以下几点：一要关注不等式的符号和应用条件;二要开展不等式定理的变形运用.尤其是教学基本不等式内容时应结合上述要点来开展.

不等式具有很高的应用价值，从数的大小关系来看可以将其视为两个数的大小比较，在求解问题时可借用基本不等式来完成数的大小比较，如对于基本不等式[a+b2≥ab] （[a≥0]，[b≥0]），通过变形可以转化为[a+b≥2ab] （[a≥0]，[b≥0]），该式子可以较好地解释a+b与[ab]的大小关系.不等式的另一个解题应用是求解最值，从不等式等号成立的条件来分析则可以获得数的最值.同样以上述基本不等式为例，分析可知当且仅当[a=b]时，[a+b]可以取得最小值，且最小值为[2ab]，该思路也是求解相关代数取值问题的重要策略之一.

而对于不等式内容的教学同样应重视其推广，以求拓宽学生的知识视野，提升学生的解决问题能力.以基本不等式[a+b2≥ab]为例，它反映的是两个正数的算术平均数大于等于它们的几何平均数，在教学中教师可以引导学生思考：若是三个或三个以上数的情形，是否同样满足该关系？对于该问题，可以采用引导探究的方式来进行.另一种变式推广则是对两个正数的分析，引导学生思考是否可以将转其换为两个正数的倒数，教学中通过对不等式的变形来完成证明，建立基本不等式的一整串变形链（均值不等式），适当拓展学生思维的深度.

四、开展系统渗透

知识之间有着紧密的联系，任何知识都不是独立存在的.不等式内容是代数的重要组成部分，从数学核心素养培养的角度来看就不应局限于向学生简单地传达不等关系，可以将本章节内容作为一个基本的研究对象，立足解题方法教学的高点，进行知识的全面、系统渗透.

如教学不等式的相关问题时，可以结合不等式的最值应用意义，将不等式与函数内容相关联.如函数[y=x+ax（a>0）]，在研究其最值时通常是借助函数的单调性，在教学时教师可以基于均值不等式的适用条件，引导学生考虑从不等式的角度来加以求解，这样就可以将不等式的前后知识相联系，构建完整的知识体系.

不等式内容中存在一些特殊的公式与定理，这些定理和公式的证明和使用均与数学知识相关联，在教学中教师可以对知识进行穿插讲解.如教学时将集合、函数渗透于不等式的解法教学中，以及在教学直线与圆的最值问题时引入不等式知识，或将解三角形应用题与不等式的解法相融合，实现不等式知识的联网教学.另外，有必要进行数学思想的渗透，如不等式转化变形过程中渗透化归思想，基于不等式问题构建新的函数时渗透构造思想，以及利用函数图像研究不等式时渗透数形结合思想，等等.

综上，培养学生的数学核心素养应以教材为基础，教学中要注重逐步将数学核心素养融合在数学的每一个模块内容中，使学生在掌握不等式知识的同时获得学科素养的提升.总而言之，核心知识的打牢是基础，知识的系统规划是关键，学科思想的合理渗透是重点.

（特约编辑 安   平）