《方程的根与函数的零点》教学设计

徐建新

[摘   要] “方程的根”是一个静态的点，等价转化为求“函数的零点”的动态过程，体现了“动”“静”转化的思想，为利用二分法求方程的近似解奠定基础 .函数零点存在性定理是判断函数零点的重要依据，教学的难点在于将“图像特征”转化为“代数表示”. 教学设计应注重分析图像特征，归纳代数表示，提炼定理，为构建灵动的数学课堂做准备.

[关键词]方程的根;函数零点;图像特征;教学设计

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）14-00013-03

一、教学目标

1. 能结合具体函数的图像，理解方程的根、相应函数图像与[x]轴的交点以及函数零点的关系，掌握函数零点的概念;

2. 能借助具体函数的图像，掌握“函数零点存在性定理”;

3. 能利用函数图像和性质判断某些函数的零点个数;

4. 能将一个方程求根问题转化为一个函数零点问题，会判断函数零点所在的区间;

5. 能体会从特殊到一般、从具体到抽象的认知学习过程，培养函数与方程、数形结合等思想，提升数学抽象、直观想象、数学运算、数学建模等数学核心素养.

二、 教学重难点

教学重点：函数零点的概念;函数零点与方程的根的联系;连续函数在某区间上存在零点的判定方法.

教学难点：用函数与方程的思想将方程问题转化为函数问题;零点存在性定理探究过程中“图像特征”转化为“代数表示”.

三、 教学过程

1.创设情境，提出问题

问题1：下列方程有几个实根？你是如何判断的？

设计意图：对于方程（1），学生可用十字相乘法、公式法、判别式法等判断方程根的个数.但对于方程（2）的“大数据”，若运用方程（1）所涉及的方法会很烦琐. 因此，可引导学生考虑二次方程与二次函数的关系，思考能否利用二次函数[f（x）=628x2+529x+107]的图像来判断根的个数.从学生熟悉的二次方程入手，降低起点. 问题导向从简到繁，充分调动学生探究未知问题的积极性，开门见山，直接引入本节课的教学内容.

2.回顾旧知，探索新法

问题2：（1）结合图1，请观察并说明二次方程[x2-2x-3=0]的根和二次函数[y=x2-2x-3]的图像与[x]轴的交点的关系;（2）复习二次方程[ax2+bx+c=0（a≠0）]的根和二次函数[y=ax2+bx+c（a≠0）]的图像与[x]轴的交点的关系;（3）请归纳方程[f（x）=0]的根与函数[y=f（x）]的图像与[x]轴的交点的关系.

（方程[f（x）=0]的根就是函数[y=f（x）]的图像与[x]轴的交点的横坐标.）

设计意图：学生已了解二次函数图像与方程根的关系，通过表格帮助学生梳理“三者”之间的关系，再提出一般问题. 三个问题从特殊到一般，从具体到抽象，渗透“从最简单、最熟悉的问题入手解决较复杂的问题”的研究思路， 有利于培养学生的归纳能力和数学抽象素养.

3.抽象概括，形成概念

根据概念“对于函数[y=f（x）]，把使[f（x）=0]的實数[x]叫作函数[y=f（x）]的零点.”向学生阐明函数[y=f（x）]的零点问题就是方程 [f（x）=0]的根问题，零点的几何意义就是函数图像与[x]轴交点的横坐标.在建立方程与函数联系的过程中，“方程的根”是一个静态的点，等价转化为求“函数的零点”的动态过程，体现了“动”“静”转化的思想.

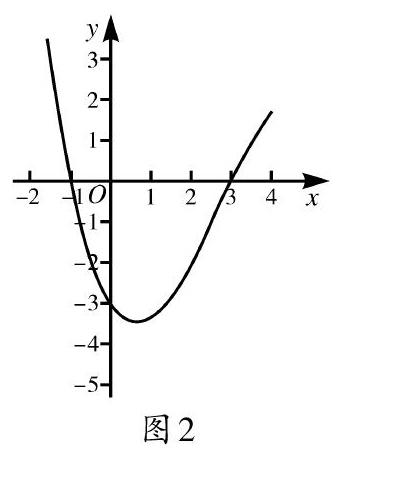
问题3：（1）观察图2，请写出函数图像与[x]轴交点的坐标及函数的零点;（2）函数的零点是点吗？

设计意图：从具体的二次函数到抽象函数的图像，加深学生对函数零点概念的理解，明确“零点是交点的横坐标，是一个实数，不是一个点，不能用交点的坐标表示”.

思考：在这些区间上，函数图像有什么共同的特点？函数值的变化有什么共同点？

（3）已知函数[g（x）=x，-3≤x≤-1，-x2+2x+4，-1

引导学生概括：题（1）（2）的函数图像是连续不断的，图像经过[x]轴，且在区间端点的函数值异号，函数有零点 .

题（3）在区间端点的函数值异号，但函数图像（如图5）是间断的，从[-1]的左侧到右侧，函数值由负值直接跳到正值，即函数图像没有经过[x]轴，函数无零点.

师生共同提炼函数零点存在性定理：

如果函数[y=f（x）]在区间[[a，b]]上的图像是连续不断的一条曲线，并且有[f（a）·f（b）<0]，那么函数[y=f（x）]在区间[（a，b）]内有零点，即存在[c∈（a，b）]，使得[f（c）=0]，这个c也就是方程[f（x）=0]的根.

设计意图：探究函数在区间[[a，b]]的端点函数值异号与零点存在性的关系，并通过题（3）强调图像应是“连续不断的一条曲线”，帮助学生将“图像特征”转化为“代数表示”，归纳出函数存在零点的条件.这个结论直观简洁，没有证明，可作为定理直接运用.

5.定理辨析，深化理解

问题5：你能改变定理的条件或结论，得到新的命题吗？请对你给出的命题判断正误，并画草图说明.

探究1（对换条件与结论）：如果函数[y=f（x）]在区间[[a，b]]上的图像是连续不断的一条曲线，且函数[y=f（x）]在区间[（a，b）] 内有零点，则[f（a）·f（b）<0] .